The importance of the tetraktys in mathematics and physics is well known, as the Clifford algebras are intimately associated with the study of geometry and physical theory. Here at the LRC, we know that this is due to the fact that the union of mathematics and physics requires understanding that there are three properties of numbers and motion: magnitude, dimension and “direction,” where each non-zero dimension has magnitude in two “directions,” which we can think of as up and down, left and right, forward and backward.
The fact that rational numbers and scalar motion have inverses (two “directions”) means that the tetraktys should also have its inverse, and, in fact, it does. We can show this by writing the numbers of the tetraktys as ratios:
20/20 = 1/1
20/20 21/20 = 1/1, 2/1
20/20 21/20 22/20 = 1/1, 2/1, 4/1
20/20 21/20 22/20 23/20 = 1/1, 2/1, 4/1, 8/1
then its inverse is obviously,
20/20 = 1/1
20/20 20/21 = 1/1, 1/2
20/20 20/21 20/22 = 1/1, 1/2, 1/4
20/20 20/21 20/22 20/23 = 1/1, 1/2, 1/4, 1/8
This may not be of interest to the LST community, because they don’t recognize scalar motion, let alone multi-dimensional scalar motion, and even if they did no doubt they would be stopped cold by the notion of super-luminal speeds.
But in the RST community, aware of the cosmic sector and its inverse speeds, the inverse tetraktys is of great interest, since it is a generalization of the multi-dimensional numbers, and their algebras, of the cosmic sector, just as the tetraktys is the generalization of those things in the material sector.
To truly understand the theoretical universe of the RST, both the tetraktys and the inverse tetraktys are necessary. Of course, this means that we need multi-dimensional numbers and units of motion that are scalar, or pseudoscalar, but, unfortunately, these don’t exist in the LST community’s system of mathematics. They have devised an imaginary number (the so-called square root of -1) to raise the dimension of scalar numbers, because they needed to stick with the 1D motion of objects, not realizing that motion without objects is also possible.
However, as we know, this has sickened their multi-dimensional algebras, forcing them to cope with trying to understand physics with nothing but scalars and vectors, or the 0D numbers of scalars and the 1D numbers of complex numbers. Because of this, most physicists and engineers would think we’ve gone batty if we start referring to multi-dimensional scalars - to them, it’s a contradiction in terms.
Nevertheless, that’s really what pseudoscalars are. So now we want to go back and replace the imaginary square root of -1, upon which the superstructure of modern mathematics has been built, with the square root of 2, which is not an imaginary number, but a very real one (no pun intended here - lol).
The way I hope we can do that is, first, by recognizing that the 3D pseudoscalar has all the properties we need to coax matter out of scalar motion: Like the 3D gravitational property of matter, with its two “directions,” in and out, the 3D pseudoscalar has 3D volume with two “directions,” expansion and contraction. Likewise, the 2D magnetic property of matter, with its two “directions,” north and south, is analogous to the 3D pseudoscalar’s 2D surface, having an inner and outer side, which cannot be separated. Finally, the 1D electrical property of matter, with its two “directions,” positive and negative, is reflected in the 3D pseudoscalar’s 1D circumference, which also has two “directions,” clockwise and counter-clockwise.
Add to this the fact that the inverse pseudoscalar is already studied in the field of inversive geometry, and we have at least two good reasons to suspect that this line of investigation is worth pursuing.
As explained recently in the New Math blog (See here), the square root of 2 turns out to be quite useful for defining numbers, in terms of the geometry of the three spheres, which correspond to -1, 0, +1, when -1 is understood to be 1, 0 is understood to be the square root of 2, and +1 is understood to be 2, the inverse of 1, and we replace these integers with the rational numbers, 1/2, 1/1, 2/1, using Larson’s concept of speed-displacement.
This may sound crazy at first, but it’s only necessary to understand that 0 doesn’t really have to be understood in the way it’s normally portrayed on the real number line, or in Cartesian coordinates. That is to say, the way we understand it in our LRC research is not like this:
-n …, -3, -2, -1, - 1/2, -1/3, … -1/n, 0, 1/n…1/4, 1/3, 1/2, 1, 2, 3, … n
where the unit distance is seen as infinitely divisible, but rather as,
1/n, …1/4, 1/3, 1/2, 1/1, 2/1, 3/1, 4/1, …n/1
where each unit is not infinitely divisible, but is discrete and has its discrete inverse unit, as in group theory. In this way, 0 does not have a place on the number line per se. Instead, it is implied by 1/1 = 0, when the binary operation of the group is changed from multiplication to addition, and the meaning of the “/” symbol becomes a “displacement” operation between the numerator and denominator, not an inverse multiplication operator.
With this much understood, we want to map the set of pseudoscalars, corresponding to the first two units of the expansion (t1-t0 = 1 and t2-t0 = 2), to the tetraktys and the inverse tetraktys, in the same way we map the rational numbers to it, using the intermediate pseudoscalar, with the unit ratio of the square root of 2, as the 0D tetraktys value, the ratio of the 1D circumferences as its 1D value, the ratio of the 2D surfaces as its 2D value, and the ratio of the 3D volumes as its 3D value.
We can use circles with differing patterns to indicate which aspect of the spheres is being symbolized, a pattern of dots for the 0D pseudoscalar, a pattern of lines for the 1D one, a pattern of squares for the 2D one, and a solid fill for the 3D one, as shown below:

Figure 1. Symbolic Notation for Radii, Circumferences, Surfaces and Volumes of Pseudoscalar Spheres with Radii r =1, r’ = (2)1/2, r’’ = 2.
First, we construct the pseudoscalar tetraktys, then the inverse pseudoscalar tetraktys:
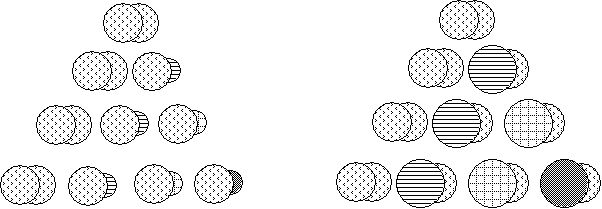
Figure 2. The Tetraktys and Inverse Tetraktys of Pseudoscalar Sphere Ratios
As it turns out, each of these pseudoscalar ratios is a power of the square root of 2. The unit ratio, which is just the ratio of the radius r’ to itself, or the square root of 2, divided by itself, is equal to 1. Letting R equal this unit ratio, we can write it as R0 = (21/2)0 = 1, because any number raised to the zero power is equal to 1. The ratio of the 1D circumferences of r’ and r, 2πr’/2πr, is equal to the square root of 2, or (21/2)1, which we can write as R1. The ratio of the 2D surfaces, 4πr’2/4πr2, is equal to 2, or (21/2)2, which we can write as R2. Finally, the ratio of the volumes, (4/3)πr’3/(4/3)πr3, is equal to 2*21/2, which we can write as R3, since 2 * 21/2 = (21/2)3.
Substituting these values of R for the graphics shown in figure 2, we can rewrite the pseudoscalar tetraktys, and its inverse, symbolically, as shown in figure 3 below:
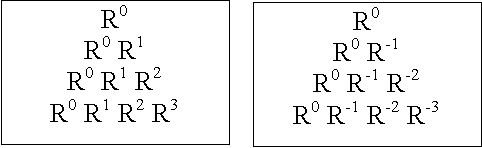
Figure 3. The Symbolic Pseudoscalar Tetraktys and Its Symbolic Inverse
This is a remarkable result, because it appears to constitute the basis for a multi-dimensional number system with no algebraic pathology, since each associated pseudoscalar algebra would presumably be as completely ordered, commutative and associative, as the well known scalar algebra.
Clearly, the R0 numbers are ordered, since the square root of 2 is a real number. The R1 numbers are ordered, because we can’t have an R1 number smaller than 1. The R2 numbers and the R3 numbers are also ordered for the same reason, because no areas and volumes smaller than the unit areas and volumes exist in the system, by definition.
Indeed, I think the proof that all these numbers are ordered, commutative and associative is trivial, so I won’t bother to show it here.
Of course, I could be wrong – and very embarrassed – again!