The Trouble With Physics
Entries by Doug (38)
Larsonian Physics and Einstein's Plague
A friend called me the other day and asked, “What is ‘Larsonian physics,’ as distinguished from ‘Newtonian physics?’” To compare the two systems (see here), it is helpful to understand Hestenes’ description of Newtonian physics. He writes: 1
Newtonian mechanics is, therefore, more than a particular scientific theory; it is a well defined program of research into the structure of the physical world…. [The foundation of the program to this day is that] a particle is understood to be an object with a definite orbit in space and time. The orbit is represented by a function x = x(t), which specifies the particle’s position x at each time t. To express the continuous existence of the particle in some interval of time, the function x(t) must be a continuous function of the variable t in that interval. When specified for all times in an interval, the function x(t) describes a motion of the particle.
This continuous function, representing the motion of an object from one location to another over time, which “expresses the continuous existence of a particle” and forms the foundation of Newtonian physics, is replaced in Larsonian physics, as developed here at the LRC, by a progression of space and time, independent of any object. When either the space or time aspect of the space|time progression oscillates, at a given point in the progression, a point in space (or time) is established, the position x of which is represented by the continuous function x = x(t) = 0 (or x = x(s) = 0); that is, the point’s spatial (or temporal) position, in the progression, no longer changes with the progression, due to the oscillation. In other words, it becomes stationary (non-progressing) in space (or time); Its fixed position, relative to the progression, is actually generated and maintained dynamically by its oscillation (as a 1D analogy, we can think of a stationary fish swimming against the current of a flowing stream.)
Thus, in the LRC’s Larsonian physics, the continuous function expresses a spatial or temporal location that had no prior existence, while in Newtonian physics, the continuous function expresses a change between pre-existing locations. Subsequently, the change that Einstein introduced into the Newtonian program replaced Newton’s ideas of absolute time and absolute space, so that spatio-temporal locations are no longer pre-existent in the Newtonian system, but are dynamically generated from a gravitational field in general relativity.
Of course, the fixed background of locations in Newton’s concept is still necessary to define motion in the quantum field theory of particle physics, where only Einstein’s special relativity is employed and his general relativity is ignored, causing the immense trouble with the attempts to unify modern physics, which is the subject of this blog: The theory of gravity generates the space and time continuum, while the theory of matter pre-supposes it, even though they are both field-theoretic constructs.
However, the important thing to understand about the LRC’s Larsonian physics is that the dynamic creation of points out of the space|time progression provides the basis for a physics of the discretium, without the need to resort to the continuous field concept, or, as Einstein would have expressed it, it provides a basis for an algebraic physics, as opposed to a physics of the continuum, or a geometric physics.
Though it’s not widely known, Einstein actually would have preferred a discretium based, or algebraic physics, but was unable to find a way to get to such a system. He was convinced, as today’s physicists are too, now, after pursuing unification as diligently as he did (even though he was mocked for doing so at the time) that the space continuum is “doomed,” as Witten puts it.2 In fact, according to Arkani-Hamed, “The idea that [the space continuum] might not be fundamental is pretty well accepted…”3 in the legacy physics community.
But, in his day, Einstein suffered alone, “plagued” with his thoughts that the assumption of a space and time continuum was probably the wrong approach, given that physical phenomena are quantized. Nevertheless, all the while, he is celebrated as the champion who revolutionized continuum physics. John Stachel, of the University of Boston’s Center for Einstein Studies, who first discovered this other side of Einstein,” explains: 4
If one looks at Einstein’s work carefully, including his published writings, but particularly his correspondence and reminiscences of conversations with him, one finds strong evidence for the existence of another Einstien, one who questioned the fundamental significance of the continuum. His skepticism seems to have deepened over the years, resulting late in his life in a profound pessimism about the field-theoretical program, even as he continued to pursue it.
What Einstein would have discovered, had he lived to study the algebraic physics that we are developing at the LRC, is that, while the continuum is something that can be conceived by the human mind, it isn’t necessary to conceive of it as an a priori construction needed to develop a discrete set of points, which was the great obstacle that baffled him. As Stachel points out, Einstein wrote to Walter Dallenbach, confirming that his former student had also correctly grasped the “drawback” of the continuum, which drawback is essentially that it seems that one needs to have a continuum in order to have a discontinuum:
The problem seems to me [to be] how one can formulate statements about a discontinuum without calling upon a continuum (space-time) as an aid; the latter should be banned from the theory as a supplementary construction, not justified by the essence of the problem, [a construction] which corresponds to nothing “real.” But we still lack the mathematical structure unfortunately. How much have I already plagued myself in this way.
Of course, the mathematics of the time were still going the opposite way. Mathematicians were happily following Dedekind and Cantor in constructing a continuum (infinite sets and smooth functions) from a discontinuum (discrete numbers). In fact, Stachel, speculates that Einstein’s doubts about the reality of the continuum stem, in part, from his reading of Dedekind, from whom he borrows his oft used phrase “free inventions of the human mind,” that did anything but endear him to Larson. Dedekind argues against the continuum by insisting that discontinuity in the concept of space does not affect Euclidean geometry in the least:
For a great part of the science of space, the continuity of its configuration is not even a necessary condition…If anyone should say that we cannot conceive of space as anything else than continuous, I should venture to doubt it and call attention to the fact that a far advanced, refined, scientific, training is demanded in order to perceive clearly the essence of continuity and to comprehend that besides rational quantitative relations also irrational, and besides algebraic, transcendental quantitative relations, are conceivable.
Of course, it was highly unlikely that Einstein was aware that Dedekind’s intellectual journey into irrational numbers and infinite sets began some fifty years previously with his exposure to Hamilton’s work, who had defined irrational numbers, but in the context of numbers derived, not from the abstract notion of a set, but from the intuition of the progression of time. And while Hamilton’s work on irrational numbers in his “Algebra of Pure Time,” is little regarded today, who could have known that it would have been eventually synthesized by Clifford with the Grassmann numbers as an “operationally interpreted” number, leading to Hestenes’ pioneering work in the recognition of geometric algebra as the unification of geometry and algebra through the geometric product.
While the bottom line can only be sketched at this point, all indications are that the mathematical structure, which Einstein pined for, that would enable him to be able to define a discontinuum, without the aid of a continuum, appears to be at hand. To be sure, he outlined major conceptual obstacles with both concepts in his letter to Dallenbach:
Yet, I see difficulties of principle here too. The electrons (as points) would be the ultimate entities in such a system (building blocks). Are there indeed such building blocks? Why are they all of equal magnitude? Is it satisfactory to say: God in his wisdom made them all equally big, each like every other because he wanted it that way? If it had pleased him, he could also have created them different. With the continuum viewpoint one is better off in this respect, because one doesn’t have to prescribe elementary building blocks from the beginnning. Further, the old question of the vacuum! But these considerations must pale beside the overwhelming fact: The continuum is more ample than the things to be descibed.
Thus, Einstein was left to plague himself with these thoughts, but now with a knowledge of Hamilton’s “algebraic numbers,” Larson’s “speed displacements,” and Clifford’s “operational interpretation” of numbers, and his multi-dimensional algebras, there is much more to work with than there was in Einstein’s day. Perhaps, it’s time to now stand with the legendary icon of physics and say:
I hope my friend would understand.[O]ne does not have the right today to maintain that the foundation [of physics] must consist of a field theory in the sense of Maxwell. The other possibility leads, in my opinion, to a renunciation of the space-time continuum and to a purely algebraic physics.
Logically, this is quite possible: The system is described by a number of integers; “Time” is only a possible viewpoint, from which the other “observables” can be considered - an observable logically coordinated to all the others. Such a theory doesn’t have to be based upon the probability concept…
Fundamental Physics in 2010
In preparing my presentation for the next lecture in the LRC Public Lecture Series, I came across a video of a talk given by Nima Arkani-Hamed, of the Institute for Advanced Studies at Princeton, entitled “Fundamental Physics in 2010.” I recognized it as a video I had started to watch once before, but became impatient with before it was over. Too bad, because it’s really good.
He explains the “crises and paradoxes” that current fundamental physics faces as well, or better even, than anyone else I’ve seen. He even explains why theorists find that space-time is emergent, something I had looked for in vain a while back. It turns out to be quite simple. Just like the 20th Century discovery of the uncertainty principle stood classical physics on its ear, because both position and momentum, which are the heart and soul of classical physics, can’t be specified to an arbitrary precision in quantum mechanics, the new crisis stands quantum mechanics on its ear, because distances smaller than the Planck length can never be observed, since doing so would require so much energy that it would warp spacetime into a black hole at that scale.
This means that, at singularities, such as black holes and the big bang, the breakdown of the spacetime fabric creates a need for a replacement of some kind. The break down of the spacetime equations at singularities means that physicists can’t speak of a time before the big bang, since it makes no sense to do so. Arkani-Hamed says, “Our theories simply break down when gravity and quantum mechanics both become important. Cool stuff.”
But then he goes on to explain how, initially, string theory was thought to be a way to get around the problem since the smallest strings were considered to be around 10-31cm, which were too big to be swallowed up by the black hole at 10-33cm. However, in 1995 it was found that strings could be points, strings or even membranes and could have any size. This was “probably, the most important theoretical development in the last twenty years,” says Hamed. “The whole dichotomy between particles and strings has disappeared…particle theories and string theories can be different facets of exactly the same thing.”
I thought this would be a really good seqway into the lecture I was preparing, so I used it. Or at least I started out to use it. By the time I was finished, it was hard to tell that the current idea of emergent spacetime was at the core of the presentation. In fact, in the end, I ended up talking more about dimensions in general, the 26 dimensions of string theory, the 10 dimensions of superstring theory, and, finally, 11 dimensions of M-theory, all of which lead to the theories of Arkani-Hamad et al (ADD theory) and Lisa Randall et al (RS theory), known generally as theories of large extra dimensions.
The reason they are called large extra dimensions is because, with M-theory, the extra dimensions of string theory no longer need be compactified to make them fit into the 1+ 3 dimensions of observed reality, but they may be as large as the universe; that is a closed loop of string, like an over inflated inner tube, may morph into a membrane and the 1+ 3 dimensions may be on its surface, with open ended strings attached like leeches, unable to escape, while closed strings easily drift off into the interior bulk of the membrane. Since closed strings are gravitons in string theory, this provides ADD theories with an alternate way to explain the relative weakness of gravity, which does not require the unification of gravity at the planck scale, at 10-33cm, but only at the much more manageable electroweak unification scale at 10-17cm. The RS theory is a variation of this where the gravitons live on another brane, the scale of which is much larger than the scale of the 1+ 3 brane, providing a warped transition for gravitons that reduces their strength.
However, you can probably imagine the difficulty of explaining all this in less than one hour, while at the same time trying to provide enough background to motivate it all. It’s one tall order and I’m not sure how well I succeeded, but in the end I tried to show how young Heisenbergs might fiddle around with dimensions themselves by taking a fresh look at the meaning of dimensions in the tetraktys, in the Grassmann numbers of Clifford algebra, and in geometry. If you’re wondering how I did justice to all that in a presentation of less than one hour, you’ll soon realize that I couldn’t.
What I hoped to show, though, was that it’s possible to see how the 26 dimensions of string theory reduce to the 10 dimensions of superstring theory, by simple inspection of the tetraktys, through the principle of duality. I didn’t even come close to doing that, but, hopefully, I managed to open the door to their curiosity enough to give them a peek at this marvelous mystery.
For those who might be interested, I will try to explain it more completely tomorrow on the New Math blog.
Fiddling Young Heisenbergs
How fast time flies. It’s been about three months since my last entry. I’ve been so busy trying to put together seminars that I’ve had to let everything else go, including blogs and research. I’ve probably lost a lot of readers as a result, especially direct feed subscribers.
The irony of the whole thing is that not one seminar has been held. The reason is not because I didn’t prepare them, but because we didn’t hold them. The official reason we didn’t hold them is due to illness and bad weather, but the real reason goes deeper than that. It turns out that we had several new comers who were invited to attend the seminars, some were physicists, some engineers, some journal editors, and some were mathematicians and professors, but they all were new. It soon dawned on me that it would be unwise to have new comers, each with some degree of curiosity mixed with scepticism, attend a meeting where advanced concepts of scalar motion were being discussed.
On the other hand, the veterans familiar with the fundamental scalar concepts wouldn’t appreciate making the effort to attend, just to hear what they already understood. As a result, illnesses and inclement weather became convenient excuses to postpone. Yet, I knew that postponing the meeting wasn’t a solution either. Sooner or later, I was going to have to find a real solution. Well, I did find one, but it has taken all this time to work it out.
What I decided to do was to hold introductory meetings at the local library and videotape them, so that later I could publish them on this site and direct new comers to them. That way, if they have enough interest, they need only visit the website and watch a few videos first, before deciding if they wanted to attend the more advanced research seminars.
However, it wasn’t as easy as it seemed it would be at first. In fact, the solution soon appeared to be more of a challenge than the problem it was designed to address. Who was going to come to the library to hear someone talk about the reciprocal system? The answer was easy, no one was. To tell you the truth, I was beginning to feel the effects of stress at this point.
I realized that I needed a strategy, and though not sure what it might be, it occurred to me that the History Channel programs on physics and cosmology, which were, and still are, being heavily promoted, must be generating a lot of interest, because people don’t spend advertising dollars unless it’s making them money. The History Channel was running advertisements on the other channels, so I figured they must be making money on their shows like “The Universe,” etc.
To make a long story short, I decided to use David Gross’s talk on “The Coming Revolution in Fundamental Physics,” which could also be titled “We think string theory is the beginning of a revolution in fundamental physics, but, after forty years, we still don’t know what the darn thing is!” as a drawing card. The reason is, of course, because he makes the point that “the conceptual block” preventing theoretical progress is a lack of a fundamental understanding of the nature of space and time.
After a real struggle, I was able to put the presentation together, make flyers, brochures, and arrangements for the library facilities. Then I took the flyers to the local university and high schools, told people at church, family, and friends, and started praying and hoping someone would show up.
Well, I’m happy to report that some did, but not until just a few minutes before the meeting was scheduled to start, which initially caused me to suffer a panic attack. Though we had some technical difficulties, we managed to record and publish the meeting as planned (see: http://www.lrcphysics.com/lrc-lectures). Hopefully, we can improve the quality of the next meetings, scheduled for Tuesday, April 1st, or April Fools day (!?!), and the first Tuesday of each month thereafter.
Fortunately, it turns out that the majority of those attending were high school students, and the interest seemed high. In Gross’s talk, he prophesies that it will probably take a “young Heisenberg, fiddling around somewhere in left field,” to make the breakthrough that will usher in the coming revolution. There were several of them there that night.
Far From the Madding Crowd
If the public at large knew what a frenzied state the theoretical physics world is in, maybe the media like the History Channel wouldn’t be able to make so much money retelling its make-believe stories in a series such as the popular Universe episodes currently being aired. As it is, they present the most outlandish theories, as if they were established fact, complete with sophisticated animations, interspersed with sound bytes of scientists talking about the big bang, black holes, dark matter, dark energy, the birth and death of stars, etc. with an air of sagacity and perspicacity that no doubt commands silent awe from the rapt lay audience.
The truth is, however, theoretical physicists are so confused that they are calling each other out like kids on a playground, for advancing wild and crazy speculation, on the one hand, or for refusing to embrace it, on the other. As we have discussed in this blog, Lee Smolin and Peter Woit recently published the controversial books, The Trouble with Physics, and Not Even Wrong, trying to explain why the legacy system of physics (LST) is in so much trouble.
This month, a Physics Today article, published online, entitled “String theory in the era of the Large Hadron Collider”, by Michael Dine, offers a detailed outline of the state of theoretical physics, from the perspective of an optimistic string theorist. However, the article isn’t so much about applying string theory to experiments at the LHC, as the title might suggest. Instead, it is an apparent attempt to associate controversial aspects of string theory research (“Landscapeology”) with the real science of the LHC, which is something Peter Woit characterizes as “jumping the shark,” referring to a concept of creative desperation, originating in Hollywood, which he borrowed from John Horgan and George Johnson, of bloggingheads.tv.
As Smolin and Woit explain in their books, and as Chad Orzel explains on his blog, Uncertain Principles:
[T]he “landscape” issue … refers to a problem that comes out of the process of trying to use string theory to unify the fundamental forces and account for the fundamental particles…observed in physics using a model that is mathematically identical to that which describes the vibrations of a piece of elastic string. Different vibrations correspond to different types of particles, and this allows you to describe everything that we see in terms of a single mathematical object.
Of course the problem is that more than three dimensions of space are required to do this. In fact, a total of 10 dimensions are required (in m-theory), and to get the extra dimensions, the theorists invent mathematical ways to “roll up” the extra dimensions at very small scales, so that the extra dimensions aren’t detectable. The problem is, there are so many ways to roll them up, mathematically, that, in Orzel’s words:
…different formulations of string theory each give slightly different values of the physical constants, and slightly different sets of extra particles that haven’t been detected yet. Which means that, while string theory lets you describe all the particles we see in terms of a single mathematical object, it doesn’t give you a unique description of the universe that we see, but rather a whole set of different possible descriptions.
Indeed, the number of ways to hide the extra dimensions is enormous, which leads to the idea of an immense “landscape” of solutions, dealing a death blow to string theory, in Woit’s adamant opinion, but not to a small community of string theorists such as Lenny Susskind and Michael Dine, who, like software engineers, insist on viewing this “bug” in the “software,” as a “feature.” The trouble is that this view has lead to some wild ideas that garners so much of the media’s attention that it causes problems within the LST community. Orzel explains:
This is where Dine, and Leonard Susskind, and a bunch of other people attempt to turn the Landscape problem from a bug into a feature. It’s great that there are all these bazillions of possible models, they say, because we can imagine that they’re all out there somewhere as different universes. And if they all exist, it’s inevitable that there should be one that happens to be just like ours, which is good, because we know we exist.
As if this weren’t enough to launch the likes of Woit off the map, now Dine, in his article, is taking it even further. He’s making “lemonade out of the Landscape,” so-to-speak, by proposing that the “Landscape business might be the key to making predictions that will be confirmed by the LHC,” says Orzel. Whether this is a Hollywood tactic like making “lemonade out of the landscape,” or “jumping the shark,” or not, is a matter of opinion, of course, but the fact is that, for many physicists, it’s very disconcerting. Orzel explains why:
[T]his ends up getting more press than areas in which actual progress is being made. And, for that matter, more popular attention than whole fields of physics that are producing fascinating and concrete results all the time. It’s kind of maddening, really.
Meanwhile, far from this “Madding Crowd,” we are quietly focusing on the basics, using Larson Reciprocal System of Physical Theory (RST).
For instance, we simply note that from Newton’s famous third law of motion, “for every action there is an equal and opposite reaction,” we can deduce that for every direction there must be an opposite direction, and, in three dimensions, there are therefore 23 = 8 directions. Larson illustrated these eight directions in what we now refer to as Larson’s cube, a 2x2x2 = 8 stack of one-unit cubes, with four diagonal lines connecting the eight corners of the stack:
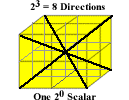
Figure 1. The Eight Directions in Larson’s Cube
Of course, the cube may be divided into two planes of four directions each, and each plane, in turn, may be divided into two lines, of two directions each. Thus, the cube is a set of eight 3D directions, or two sets of 4 2D directions, or four sets of 2 1D directions, and counting the common intersection of all these, as a set of no directions, we get another version of the four vector spaces of the octonions, where Hestenes’ has focused his career, and where string theorists focus their attention, albeit bedeviled by the Landscape:
23 = 1 + 4 + 2 + 1 = 8.
John Baez is fascinated by the mystery of these numbers too, but, being in the midst of the “Madding Crowd,” he can’t see these eight 3D directions, as we are seeing them now. He sees them as Clifford first saw them,
23 = 1 + 3 + 3 + 1 = 8
where the first set contains the real numbers, the second set the complex numbers, the third set the quaternion numbers, and the fourth set the octonion numbers. Mathematicians came up with the ad hoc inventions of negatives and imaginaries to make these different types of numbers possible, and the physicists were able to use them to good effect for a while, but now theoretical confusion reigns in their midst.
Hestene’s has notably contributed to clarifying the language of physics, through his work, even though it’s acceptance has been slow in coming. However, his great simplification of the equations of physics, equations based for the most part on complex numbers, comes from replacing the negatives and imaginaries of these number systems with another ad hoc invention, the geometric product. Unfortunately, he too fails to recognize that the four linear spaces of his geometric algebra are not necessarily confined to a space of scalars, a space of three vectors, a space of three bivectors, and a space of trivectors.
Only in the work of Larson does the insight emerge that there is another possibility. This is too bad, because if these really smart people could be persuaded to leave the madding crowd, and take up this new approach, I’m sure that they would be able to readily construct the simple scalar algebra (and the scalar calculus) that is needed to move forward. As it is, without understanding Hamilton’s early work and Larson’s obscure work extending it, such an idea would clearly appear absurd to these intellectual hunks, even if they knew about it. So, for good or ill, it is left to us scrawny intellects, weak but with relatively strong faith, to keep on keeping on, as best we can, far from the madding crowd.
The Intuition vs. Formalism of Mathesis
In discussing the trouble with physics, we always come down to the fundamental problem: We don’t understand how nature is both continuous and discrete at the same time. Our modern physical theories have to be either discrete, like quantum mechanics, or continuous, like general relativity. Some theorists, like string theorists, seek to make the discrete continuous, while others, like the loop theorists, seek to make the continuous discrete. Still others, like the particle theorists, seek to keep on keeping on, in search of the ultimate discrete answer, the illusive “God particle.”
It’s an amazing thing to contemplate the billions of dollars mankind is willing to spend to fund the efforts of these relatively small groups of advanced thinkers, in the hope that one of them will figure out how nature does it. What a sight it makes in our minds!
However, in the 19th Century, there was a tiny group of mathematicians, contemplating these things as well. Although, Sir William Rowan Hamilton, Hermann Gunther Grassmann, and William Kingdom Clifford didn’t think of themselves as a group, much less as a group working to solve the mystery of the continuous/discrete duality of nature. Such a dichotomy in nature wasn’t even suspected in their day, but for them the quest to unify the numbers of algebra and the magnitudes of geometry amounted to the same daunting challenge.
For Grassmann, a German high school teacher, the vision was one of a universal geometric calculus, which has finally been realized, in modern times, primarily through Hestenes’ recognition of Clifford’s contribution, wherein he (Clifford) brought the ideas of Hamilton’s quaternions and Grassmann ‘s exterior algebra together in what eventually emerged as Clifford algebras. Hestenes’ vision, he realized in retrospect, was the same as Grassmann’s: “a universal geometric calculus to serve as a unifed language for mathematics and physics.” This “grand vision for mechanics,” asserts Hestenes, “has recently been utterly fulfilled with a complete reformulation of the subject in terms of geometric algebra.” He writes in a paper entitled “Grassmann’s Vision,” that
…geometric calculus embraces a greater range of mathematics than any other mathematical system, including linear and multilinear algebra, projective geometry, distance geometry, calculus on manifolds, hypercomplex function theory, differential geometry, Lie groups and Lie algebras. Geometric calculus has also fulfilled Grassmann’s vision of a universal language for physics. Besides integrating the mathematical formulations of mechanics, relativity and electrodynamics, it has revealed a geometric basis for complex numbers in quantum mechanics.
Yet, this “utter” fulfillment of the “grand vision” of a “unified language for mathematics and physics” clearly has not had much impact on the fundamental problem of the theoretical physicists: The challenge of explaining the unification of the discrete and continuous aspects of nature remains unanswered. Maybe it’s too early to make this judgement. It takes many years for a new development like this to take its place in the tool box of physicists. Yet, even if it does become more widely accepted, it seems clear that simplifying and clarifying the formalisms of quantum mechanics and general relativity doesn’t make the two theories compatible with one another.
They say that the definition of insanity is doing the same thing over and over again, but expecting different results. Yet, that’s what some in the world of theoretical physicists seem to be doing. They seek to find the solution to the crisis in theoretical physics, by reformulating the current theories, over and over again. One of the latest in these attempts was discussed recently on Peter Woit’s blog, Not Even Wrong. It is Chris Isham’s effort to reformulate quantum mechanics, using something called “topos theory.”
In an article entitled “Topos or Not Topos,” Govert Schilling explains that, according to Isham, topos theory “is not a quantum gravity theory itself, but a set of tools to build new theories. It’s a deep and beautiful mathematical framework - a new kind of logic that we could try to apply to the physical world.” Schilling adds, “Isham’s hope is that the new approach will lead to a reformulation of quantum theory, which would pave the way for a decent theory of quantum gravity, without ugly infinities.”
However, Nobel Prize winning physicist Gerard ’t Hooft of Utrecht University in the Netherlands insists that yet another mathematical language is irrelevant. Consequently, he thinks that Isham’s new formalism isn’t likely to be very useful. Schilling quotes ‘t Hooft’s expression of skepticism:
Our biggest problem is how to formulate our questions,” he says. “What exactly do you want to know, and which questions are you able to answer? Isham believes another mathematical language may help, but I don’t think so. It sounds a bit as if describing the world in German is better than in Chinese.
Others, like Robbert Dijkgraaf of the University of Amsterdam, are likewise skeptical. Schilling quotes his opinion of Isham’s approach as a “long shot,” even though it “provides a fundamental way of describing quantization.” Woit too expresses doubt. He writes:
I have to say that, like ‘t Hooft and Dijkgraaf who are quoted in the article, I’m skeptical about this kind of thing, since topos theory is such a general formalism that I don’t see how it is going to provide the sort of non-trivial new idea that people are looking for.
Hence, it seems clear to skeptics, at this point in time, that a new mathematical formalism, or new language, for physics, no matter how good it might be, cannot overcome the limitations now facing physicists.
But perhaps the reason why a new formalism is unlikely to help much is especially easy to understand, when we realize that the discrete/continuous duality of nature is not only reflected in the magnitudes of nature, but also in algebra itself. Ironically enough, something that is not generally recognized today is that Hamilton’s contributions to the modern mathematical formalisms of mathematics and physics, as fundamental and indispensable as they are, were nevertheless viewed by him, at least early on in his career, as almost repugnant expedients, as long as no intuitive science of numbers, or algebra, exists.
The powerful genius of this man was troubled by the fact that, while geometry is firmly grounded in the science of space, algebra has no similar foundation, but contains inconsistencies and even contradictions. In the introductory section of his remarkable paper, “Theory of Conjugate Functions, or Algebraic Couples; with a Preliminary and Elementary Essay on Algebra as the Science of Pure Time,” Hamilton describes his complaint, by first making the clear distinction between formalism, which he refers to as philologicism, and theory, which he regards as contemplated truth:
The Study of Algebra may be pursued in three very different schools, the Practical, the Philological, or the Theoretical, according as Algebra itself is accounted an Instrument, or a Language, or a Contemplation; according as ease of operation, or symmetry of expression, or clearness of thought, (the agere, the fari, or the sapere,) is eminently prized and sought for. The Practical person seeks a Rule which he may apply, the Philological person seeks a Formula which he may write, the Theoretical person seeks a Theorem on which he may meditate.
The felt imperfections of Algebra are of three answering kinds. The Practical Algebraist complains of imperfection when he finds his Instrument limited in power; when a rule, which he could happily apply to many cases, can be hardly or not at all applied by him to some new case; when it fails to enable him to do or to discover something else, in some other Art, or in some other Science, to which Algebra with him was but subordinate, and for the sake of which and not for its own sake, he studied Algebra.
The Philological Algebraist complains of imperfection, when his Language presents him with an Anomaly; when he finds an Exception disturb the simplicity of his Notation, or the symmetrical structure of his Syntax; when a Formula must be written with precaution, and a Symbolism is not universal.
The Theoretical Algebraist complains of imperfection, when the clearness of his Contemplation is obscured when the Reasonings of his Science seem anywhere to oppose each other, or become in any part too complex or too little valid for his belief to rest firmly upon them; or when, though trial may have taught him that a rule is useful, or that a formula gives true results, he cannot prove that rule, nor understand that formula: when he cannot rise to intuition from induction, or cannot look beyond the signs to the things signified.
If we did not know better, we would think he was referring to the theory of quantum mechanics found in modern theoretical physics, not the theory of algebra. However, the same perplexing situation existed then in algebra that exists today in physics; that is, the formula of quantum physics, the wave equation, gives true results, but, in reality, physicists have no clue as to what the foundation of quantum physics might be. In Hamilton’s view, the reasonings of algebraic science were just as perplexing. The rules for adding, subtracting, multiplying and dividing worked, but the mathematician couldn’t “rise to intuition from induction,” by “looking beyond the signs to the things signified,” any more than the modern physicist can understand nature today, by studying the laws of quantum mechanics. In his paper, Hamilton clearly describes the problems of algebra he seeks to address:
These remarks have been premised, that the reader may more easily and distinctly perceive what the design of the following communication is, and what the Author hopes or at least desires to accomplish. That design is Theoretical, in the sense already explained, as distinguished from what is Practical on the one hand, and what is Philological upon the other.
The thing aimed at, is to improve the Science, not the Art nor the Language of Algebra. The imperfections sought to be removed, are confusions of thought, and obscurities or errors of reasoning; not difficulties of application of an instrument, nor failures of symmetry in expression. And that confusions of thought, and errors of reasoning, still darken the beginnings of Algebra, is the earnest and just complaint of sober and thoughtful men, who in a spirit of love and honour have studied Algebraic Science, admiring, extending, and applying what has been already brought to light, and feeling all the beauty and consistence of many a remote deduction, from principles which yet remain obscure, and doubtful.
For it has not fared with the principles of Algebra as with the principles of Geometry. No candid and intelligent person can doubt the truth of the chief properties of Parallel Lines, as set forth by Euclid in his Elements, two thousand years ago; though he may well desire to see them treated in a clearer and better method. The doctrine involves no obscurity nor confusion of thought, and leaves in the mind no reasonable ground for doubt, although ingenuity may usefully be exercised in improving the plan of the argument.But it requires no peculiar scepticism to doubt, or even to disbelieve, the doctrine of Negatives and Imaginaries, when set forth (as it has commonly been) with principles like these: that a greater magnitude may be subtracted from a less, and that the remainder is less than nothing; that two negative numbers, or numbers denoting magnitudes each less than nothing, may be multiplied the one by the other, and that the product will be a positive number, or a number denoting a magnitude greater than nothing; and that although the square of a number, or the product obtained by multiplying that number by itself, is therefore always positive, whether the number be positive or negative, yet that numbers, called imaginary, can be found or conceived or determined, and operated on by all the rules of positive and negative numbers, as if they were subject to those rules, although they have negative squares, and must therefore be supposed to be themselves neither positive nor negative, nor yet null numbers, so that the magnitudes which they are supposed to denote can neither be greater than nothing, nor less than nothing, nor even equal to nothing.
It must be hard to found a Science on such grounds as these, though the forms of logic may build up from them a symmetrical system of expressions, and a practical art may be learned of rightly applying useful rules which seem to depend upon them.
So, then, what’s the answer? How do we “found a Science” of algebra that will enable us to “rise to intuition from induction?” As it turns out, Hamilton’s answer to this question is the same as Larson’s answer to the similar question, asked in relation to physics: The answer is to be found in the recognition that numbers correspond to the order of progression, as well as to the magnitudes of isolated quantities. Only on this basis, Hamilton was convinced, could algebra rise to the level of science, comparable to the science of geometry. Yet, whether or not this conclusion is justified, the argument that, without a more intuitive basis, algebra causes reason to stare, is powerful. He writes:
So useful are those rules, so symmetrical those expressions, and yet so unsatisfactory those principles from which they are supposed to be derived, that a growing tendency may be perceived to the rejection of that view which regarded Algebra as a Science, in some sense analogous to Geometry, and to the adoption of one or other of those two different views,which regard Algebra as an Art, or as a Language: as a System of Rules, or else as a System of Expressions, but not as a System of Truths, or Results having any other validity than what they may derive from their practical usefulness, or their logical or philological coherence.
Opinions thus are tending to substitute for the Theoretical question,—“Is a Theorem of Algebra true?” the Practical question,—“Can it be applied as an Instrument, to do or to discover something else, in some research which is not Algebraical?” or else the Philological question,—“Does its expression harmonise, according to the Laws of Language, with other Algebraical expressions?”
Yet a natural regret might be felt, if such were the destiny of Algebra; if a study, which is continually engaging mathematicians more and more, and has almost superseded the Study of Geometrical Science, were found at last to be not, in any strict or proper sense, the Study of a Science at all: and if, in thus exchanging the ancient for the modern Mathesis, there were a gain only of Skill or Elegance, at the expense of Contemplation and Intuition.Indulgence, therefore, may be hoped for, by any one who would inquire, whether existing Algebra, in the state to which it has been already unfolded by the masters of its rules and of its language, offers indeed no rudiment which may encourage a hope of developing a Science of Algebra: a Science properly so called: strict, pure and independent; deduced by valid reasonings from its own intuitive principles; and thus not less an object of priori contemplation than Geometry, nor less distinct, in its own essence, from the Rules which it may teach or use, and from the Signs by which it may express its meaning.
Hamilton found that the “rudiment” of the less than inspiring existing algebra, “which may encourage a hope of developing a science of algebra,” is “the intuition of time.” He explains how he arrived at this conclusion:
This belief involves the three following as components: First, that the notion of Time is connected with existing Algebra; Second, that this notion or intuition of Time may be unfolded into an independent Pure Science; and Third, that the Science of Pure Time, thus unfolded, is co-extensive and identical with Algebra, so far as Algebra itself is a Science. The first component judgment is the result of an induction; the second of a deduction; the third is the joint result of the deductive and inductive processes.
Hamilton argues the first point, that time is connected with existing algebra, by observing the nature of calculus, which has to do with change over time, a continuous progression:
The argument for the conclusion that the notion of Time is connected with existing Algebra, is an induction of the following kind. The History of Algebraic Science shows that the most remarkable discoveries in it have been made, either expressly through the medium of that notion of Time, or through the closely connected (and in some sort coincident) notion of Continuous Progression. It is the genius of Algebra to consider what it reasons on as flowing, as it was the genius of Geometry to consider what it reasoned on as fixed.
Euclid defined a tangent to a circle, Apollonius conceived a tangent to an ellipse, as an indefinite straight line which had only one point in common with the curve; they looked upon the line and curve not as nascent or growing, but as already constructed and existing in space; they studied them as formed and fixed, they compared the one with the other, and the proved exclusion of any second common point was to them the essential property, the constitutive character of the tangent.
The Newtonian Method of Tangents rests on another principle; it regards the curve and line not as already formed and fixed, but rather as nascent, or in process of generation: and employs, as its primary conception, the thought of a flowing point. And, generally, the revolution which Newton made in the higher parts of both pure and applied Algebra, was founded mainly on the notion of fluxion, which involves the notion of Time. Before the age of Newton, another great revolution, in Algebra as well as in Arithmetic, had been made by the invention of Logarithms; and the “Canon Mirificus” attests that Napier deduced that invention, not (as it is commonly said) from the arithmetical properties of powers of numbers, but from the contemplation of a Continuous Progression; in describing which, he speaks expressly of Fluxions, Velocities and Times.
In a more modern age, Lagrange, in the Philological spirit, sought to reduce the Theory of Fluxions to a system of operations upon symbols, analogous to the earliest symbolic operations of Algebra, and professed to reject the notion of time as foreign to such a system; yet admitted that fluxions might be considered only as the velocities with which magnitudes vary, and that in so considering them, abstraction might be made of every mechanical idea. And in one of his own most important researches in pure Algebra, (the investigation of limits between which the sum of any number of terms in Taylor’s Series is comprised,) Lagrange employs the conception of continuous progression to show that a certain variable quantity may be made as small as can be desired.
And not to dwell on the beautiful discoveries made by the same great mathematician, in the theory of singular primitives of equations, and in the algebraical dynamics of the heavens, through an extension of the conception of variability, (that is, in fact, of flowingness,) to quantities which had before been viewed as fixed or constant, it may suffice for the present to observe that Lagrange considered Algebra to be the Science of Functions, and that it is not easy to conceive a clearer or juster idea of a Function in this Science, than by regarding its essence as consisting in a Law connecting Change with Change.
But where Change and Progression are, there is Time. The notion of Time is, therefore, inductively found to be connected with existing Algebra.
That algebra, connected with time, can be “unfolded in an independent pure science,” is a logical deduction from the intuition that only three possibilities exist in relation to different moments of time: One moment may be identified as the same, earlier than, or later than another. Hamilton explains:
The argument for the conclusion that the notion of time may be unfolded into an independent Pure Science, or that a Science of Pure Time is possible, rests chiefly on the existence of certain a priori intuitions, connected with that notion of time, and fitted to become the sources of a pure Science; and on the actual deduction of such a Science from those principles, which the author conceives that he has begun.
Whether he has at all succeeded in actually effecting this deduction, will be judged after the Essay has been read; but that such a deduction is possible, may be concluded in an easier way, by an appeal to those intuitions to which allusion has been made. That a moment of time respecting which we inquire, as compared with a moment which we know, must either coincide with or precede or follow it, is an intuitive truth, as certain, as clear, and as unempirical as this, that no two straight lines can comprehend an area.
The notion or intuition of Order in Time is not less but more deep-seated in the human mind, than the notion of intuition of Order in Space; and a mathematical Science may be founded on the former, as pure and as demonstrative as the science founded on the latter. There is something mysterious and transcendent involved in the idea of Time; but there is also something definite and clear: and while Metaphysicians meditate on the one, Mathematicians may reason from the other
In our own work, following Larson, we have developed a new kind of algebra at the LRC, based on continuous progression and the operational interpretation of number, but only recently did we discover that no less a figure than Hamilton had investigated and justified the mathematics of progression. Of course, there are major differences, but the idea of displacements, the primary concept of the mathematical science of time, as Hamilton called it, is the central idea of both. Hamilton’s conclusion was that the mathematical science of time is coextensive and identical with the mathematical science of algebra; that is, the mathematical science of order in progression is just that, a science, not a formalism. He writes:
That the Mathematical Science of Time, when sufficiently unfolded, and distinguished on the one hand from all actual Outward Chronology (of collections of recorded events and phenomenal marks and measures), and on the other hand from all Dynamical Science (or reasonings and results from the notion of cause and effect), will ultimately be found to be co-extensive and identical with Algebra, so far as Algebra itself is a Science: is a conclusion to which the author has been led by all his attempts, whether to analyse what is Scientific in Algebra, or to construct a Science of Pure Time.
It is a joint result of the inductive and deductive processes, and the grounds on which it rests could not be stated in a few general remarks. The author hopes to explain them more fully in a future paper; meanwhile he refers to the present one, as removing (in his opinion) the difficulties of the usual theory of Negative and Imaginary Quantities, or rather substituting a new Theory of Contrapositives and Couples, which he considers free from those old difficulties, and which is deduced from the Intuition or Original Mental Form of Time: the opposition of the (so-called) Negatives and Positives being referred by him, not to the opposition of the operations of increasing and diminishing a magnitude, but to the simpler and more extensive contrast between the relations of Before and After, or between the directions of Forward and Backward; and Pairs of Moments being used to suggest a Theory of Conjugate Functions, which gives reality and meaning to conceptions that were before Imaginary, Impossible, or Contradictory, because Mathematicians had derived them from that bounded notion of Magnitude, instead of the original and comprehensive thought of Order in Progression.
What Hamilton discovered, that the opposition of negatives and positives may be referred to relations of before and after, instead of “the operations of increasing and diminishing a magnitude,” and that “pairs of moments” suggest a “theory” that “gives reality and meaning to conceptions that were before imaginary, impossible, or contradictory,” leads to a new understanding, which is that the bounded notion of magnitude, an isolated quantity, is limited and misleading compared to the “original and comprehensive thought of order in progression.”
Nevertheless, as far as I can tell, this idea, so vital to Hamilton, has lain dormant ever since the day he discovered it, even though it clearly may be, to put it in the words of Woit above, “the sort of non-trivial new idea that everybody is looking for.”
The prospect that the new idea of a mathematical science of progression opens the door to understanding the mystery of nature’s discrete/continuous duality was not apparent until Larson’s work revealed the true nature of space: It is simply the reciprocal of time. Given the power of understanding that the mathematical science of time is coextensive to, and identified with, the science of algebra, as discovered by Hamilton intuitively, prepares us in a remarkable way to understand the reciprocal relation of two such progressions, which consequently forms the basis for the structure of the physical universe, a structure consisting of nothing but motion.
At the same time, it gives us a renewed appreciation for the value of intuition in science. One dimension of that insight that we probably should always keep in mind is that many times great things are brought to pass by very small means.