The Larson Research Center

In the Newtonian system of physical theory, which we’ll rather presumptuously refer to as the legacy system of physical theory (LST), for brevity’s sake, everything is based on the function x(t), given Newton’s laws of vectorial motion, while in the Reciprocal System of Physical Theory (RST), everything is based on the function x(t), and a new function, t(x), given the new interpretation of the nature of space/time, as the two reciprocal aspects of scalar motion.

In the LST, the focus on forces to describe and explain the relationships between the properties of mass, magnetic moment, and electrical charge, necessarily involves understanding the coordinate path of an entity, because changes in the coordinate path, or location, of a physical entity constitute the condition which gives rise to force, given Newton’s laws. However, the science of dimensional analysis, initially employed in the investigation of forces, quickly becomes tedious and unwieldy in this respect.

Fortunately, however, it was discovered that such studies could be simplified to a great extent by expressing these relationships in terms of energy, instead of force. Thus, the total energy of a system, in terms of its kinetic and potential energy, can be formulated as Legrangian equations of motion, leading to Hamiltonian mechanics, taking advantage of the principle of least action to simplify the study of forces.

Consequently, the Legrangian and Hamiltonian formalisms of mechanics have led the way to understanding how the properties of physical entities are related, including easing the transition from the concept of force associated with a coordinate path, an x(t) function, to the concept of force associated with a coordinate field, written as a q(x) function, where x represents both space and time coordinates. This mathematical reinterpretation of the x(t) function, enabled the reformulation of Newton’s universal law of gravity into a function of a field, the G field, the gravitational field, and eventually, it enabled Maxwell’s formulation of the magnetic and electric equations of motion as fields as well, the E and B fields, and their unification in the electromagnetic field theory.

The dramatic success of these and subsequent developments have led to unimaginable advances in engineering and technology that have harnessed this knowledge for the material benefit of mankind, and led to the enshrining of theoretical physics as the foundation of modern civilization and enlightenment. Interestingly enough, it has also led to the conviction among physicists that the “unreasonable effectiveness of mathematics in physics” is the hallmark of modern theoretical physics.

However, it should be clear that removing the requirement that we need a background of space and time coordinates in order to define motion, and moving up to a more fundamental understanding of the nature of space and time, as the reciprocal aspects of a universal motion, existing in three dimensions, and in discrete units, is going to have an enormous impact on the need for these complex mathematical formulations, used so effectively in the LST research program, namely the ubiquitous use of partial differential equations.

Moreover, since the primary aim of the RST program is not to determine how the given properties of physical entities relate to one another, as it is in the LST program, but rather to determine how the observed properties of physical entities emerge from more fundamental entities, namely the discrete units of space/time, the mathematics of the RST most likely will be dramatically simplified, at least initially, but, by the same token also, it will likely exhibit another surprising and enlightening aspect of the “unreasonable effectiveness of mathematics in [theoretical] physics.”

In the RST definition of motion, the postulate of the reciprocal relation of space and time, and discrete units of motion, constitute a major move of physics into the rational number system that is closed under non-zero division. Since the progression ratio of space and time can never be zero (time and space never stop progressing), this means that the system itself is indeed closed, containing its own boundary. More importantly, this means that the mathematics of the RST is a group, the ultimate closure structure.

The significance of this is that RST mathematics can be encapsulated in one sentence: the RST mathematics is the set of all properties that can be conserved by the rational number system group. So, just as special relativity is the study of all properties conserved under the Lorentz group of transformations, the RST is the study of all properties conserved under the rational number system group of transformations. The basic concept of group is symmetry, and, as mentioned in previous posts in this series, Emmy Noether proved that symmetry is the conservation law of nature. This is why mathematical groups have such predictive power and have assumed such a prominent role in modern theoretical physics, starting with Murray Gell-Mann’s prediction of the omega minus particle on the basis of completing the symmetry of a group. [10]

With the progression ratio ds/dt defining the mathematics of RST motion, the group structure implies that the inverse ratio, dt/ds, is also closed. Thus, the symmetry of the RST is the perfect symmetry of the group, which is ds/dt = dt/ds = 1/1. With the numerical possibility of zero eliminated, the datum of the system becomes this operational definition of unit magnitude, and any displacement of the progression rate of space or time, relative to its reciprocal aspect, “breaks” the fundamental symmetry of the unit ratio, but conserves it in the symmetry of the group. In other words, |1/n| is equal to |n/1|, because there is no way to distinguish the two magnitudes from the point of view of the datum of the system, 1/1.

This is interesting, because it sheds new light on the meaning of the natural and integer number systems as well as the meaning of Euclidean geometry, which is assumed to be a property of the universe of motion, in the second fundamental postulate of the system. The difference between the natural number system and the integer number system is found in the negative numbers of the integer system that don’t exist in the natural number system. Both the natural number system and the integer number system start with the number zero, an enigmatic concept to say the least, but one we have come to take for granted.

However, because the negative numbers are the mirror image of the positive numbers in the integer system, zero stands between -1 and 1 in that system. Yet, while zero quantity makes some sense in the natural number system, it is completely out of place in the integer system, since, strictly speaking, zero is not actually a number and therefore cannot be an integer. The Merriam-Webster dictionary definition of the word integer reveals the subtlty involved. It defines an integer as, first, “any of the natural numbers, the negatives of these numbers, or zero,” which explicity excludes zero as a natural number, and, secondly, as “a complete entity,” something, by definition, zero is not.[11]

Hence, something is obviously askew in our need for the quasi-number zero, but it’s difficult to define exactly what it is. Obviously, we can’t manage without it, yet we can’t strictly define it as a number either. As it turns out, in the RST definition of motion, the quasi-number zero doesn’t exist. In listing the integers of the integer system defined by the operational definition of an integer, zero disappears. This is because, operationally, the definition of the zero datum, the system’s point of reference, is 1 = 1/1; that is, the difference between negative 1 and positive 1 is the operationally defined difference between 1/2 and 2/1, and the operational magnitude that stands between these two magnitudes is 1/1, not zero. Hence the integer number system is the set of integers operationally defined by the ratio of natural numbers, which excludes zero, because it is not a natural number. It is true that it is included in the mainstream list of integers, but including it in the list of integers is misleading, if the difference between an operationally defined magnitude and a quantitatively defined magnitude is not understood.

There is another important aspect to this number system as well. Not only may integer magnitudes be interpreted operationally, or quantitatively, but also the difference can go the other way, wherein the ratio of two integers may be understood operationally or quantitatively as well. Thus, in the quantitative interpretation, the ratio of 1/2 = .5 is not a magnitude equal to 2/1 = 2. However, in the operational interpretation, the magnitude of the ratio 1/2 = 1 is a magnitude equal to the ratio 2/1 = 1, just as the unequal magnitude on one side of a pan balance is no different than the same imbalance, if it were to be placed on the other side of the balance. The only difference is which side of the balance the magnitude happens to be found. We can distinguish this in the number system by the use of the “direction” concept of positive and negative, and so we do in the integer number system, but there is no difference in the magnitudes themselves. Hence, it makes no sense to write operationally defined magnitudes as ratios of signed integers. Operationally defined integers are all simply magnitudes. The “direction” we use to distinguish them is only an indication of which “direction” in the ratio, relative to the unit ratio, the magnitude lies. We can say one is “above” unity, while the other is “below” unity, or we can say that one is “positive” and the other “negative,” but relative to the datum of the system, 1/1, there is no material difference in the magnitudes themselves.

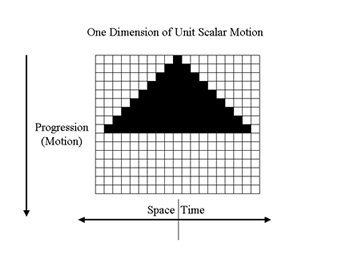
One method that has been found to encapsulate the nature of this relationship of the integer number system to the rational number system is an adaptation of a cellular automata (CA) rule, designated rule 254, by Steven Wolfram.[13] This automaton is, to Wolfram, one of the most uninteresting of all automata generated by CA rules: a perfectly symmetrical triangle as shown in figure 1. However, by slightly modifying the meaning of the output of rule 254, we obtain an operational definition of integer magnitudes; that is, if we define the center column of rule 254, as the demarcation between the reciprocal integers, the operation indicator served by the ‘/’ symbol in mathematical notation of rational numbers, and then define the total number of units to the left of the center column as one integer and the total number of units to the right of center as the corresponding reciprocal integer, then as the rule proceeds and adds one unit on each side of center to the accumulated total number of units on either side, as each successive row is generated by the rule, the result is a visual graph of the 1/1 reference datum of the rational number system expressed as a progression of reciprocal integers, the ratio of which is constant at 1/1.

Figure 1. Wolfram’s CA Rule 254

Thus, we start with row 1, which contains one black cell, then row 2 has two black cells on either side of the operation symbol, or 1/1. When row 3 appears, there are 2 black cells on either side, or 2/2, which is also a 1/1 ratio, and so on, ad infinitum. Therefore, the output of CA rule 254 is the integer 1, operationally defined as 1 = 1/1, which is actually the reference datum of the rational number system, sometimes mistakenly denoted as zero, as explained above.

To generate the integer commonly designated 1, or -1, which is really 1 = 1/2, or 1 = 2/1, as also explained above, we need to change the rule. Now, there may, or may not, be a CA rule to do this, but, nevertheless, there is an algorithm, dubbed the progression algorithm (PA), that will reproduce the pattern of CA rule 254 and also a deviation from this pattern, which will produce the 1/2 ratio, or the 2/1 ratio.

The PA adopts the operationally interpreted rational output of CA rule 254, and designates the left side integer as the space progression, and the reciprocal, or right side integer, as the time progression. Thus, the PA corresponding to CA rule 254 is a representation of the RST’s natural reference system as defined by Larson, as shown in figure 2.

Figure 2. The Natural Reference System PA.

Obviously, we can use this to study the properties of the system. For instance, the sides of the triangle represent the unit ratio boundary, since any change in the ratio from 1/1, would immediately change the location of the sides, breaking the symmetry of the system in the process. Also, we can visually see the meaning of “direction” in our system, as the left unit boundary is distinct from the right unit boundary relative to the center column, but at the same time they are one and the same boundary, viewed from different points of view, giving us at once a clear understanding of the meaning of the concept of reciprocity, as the symmetrical growth of one entity with two reciprocal aspects.

We also clearly see the concept of discrete units of space and time in the PA, but only as the reciprocal aspects of the units of progression, or the rows. Without the reciprocal integers, we would lose the definition of the row, without the row, we don’t have a progression. Therefore, one cannot exist without the other. There are other properties of the PA, which give us great insight into the RST, but we will have to wait to consider these until we can take up the subject again in the next part of this article.

While the mathematics of the RST are based on the deceptively simple set of rational numbers, there is a lot here that we are not used to perceiving in connection with this number system, and also, the fundamental symmetry of the system portends great things to come, for as some great philosophers have noted in the past, many times, out of that which is small, proceedeth that which is great.

(See also: Larson’s New System of Physical Theory - Part V - Larson’s New System of Physical Theory - Part I - Larson’s New System of Physical Theory - Part II - Larson’s New System of Physical Theory - Part III)