Part V - Larson’s New System of Physical Theory
As we have seen, in the RST, the initial state of the universal progression, the space/time unit ratio of scalar motion, is 1/1, or an increase of one unit of space for every unit of time increase. The result of this condition is nothing; that is, without some deviation from unity, the perfect symmetry of the initial state is a perfect void, or, we might say, nothing is perfect. However, the first fundamental postulate of the system posits the existence of discrete units of motion, existing in three dimensions. Therefore, we must assume that this perfect symmetry is “spontaneously” broken. The idea of spontaneous symmetry breaking (SSB) is a cornerstone of modern theoretical physics. It occurs in a situation, where, given a symmetry in the equations of motion, solutions exist that are not symmetric. Thus, a non-symmetrical solution to the universal progression equation, represented by the unit ratio PA, is any ratio wherein the magnitude in the denominator or the numerator of the ratio is greater than one. In other words, the symmetry of the initial state is broken when the space/time ratio of the motion is something other than 1/1, such as when it is 1/n, or n/1, where n>1.
Since in the universe of motion, the fundamental entities are units of motion, we cannot add units of space or units of time to the progression ratio directly. Therefore, any deviation from the symmetry of the unit ratio must occur as a result of the dynamics of the motion itself. Fortunately, such an alteration in the condition of the progression can occur, if the “direction” of the progression reverses; that is, if the continuous pattern of increase in the number of units in the space or time aspect of the progression is changed, from a pattern of continuous increase to an alternating pattern of increase/decrease, with respect to the reciprocal aspect of the progression, then a displacement in the magnitude of the reciprocal aspect of the progression will occur, breaking the symmetry of the unit ratio. The result will be a change from the 1/1 progression ratio to a 1/2, or 2/1, progression ratio, depending upon which aspect of the progression changes its “direction” pattern.
In figure 3, a “direction” reversal occuring in the space aspect of the progression produces a 1/2 space/time ratio in the PA. Notice that the “direction” of the arrows in the space cells indicate a continual “direction” reversal in the space progression, thereby constraining the increase in the space aspect of the progression (the left side of the diagram) relative to the time aspect, which increases normally as the progression proceeds downward. Hence, the space aspect alternately increases and decreases, confining it to one unit of space, and decreasing the number of times it increases (the arrow points to the left) by half. Therefore, after n units of progression, the number of units of time increase is always n, but the number of units of space increase is 1/2 n, producing a space/time ratio of 5/10 after 10 units of progression, a ratio of 10/20 after 20 units and so on, ad infinitum.
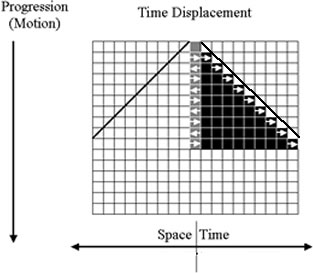
Figure 3. 1/2 Time Displacement PA
Alternatively, if the “direction” reversals occur in the time aspect of the progression, the displacement occurs in the reciprocal, or space, aspect, producing a space/time ratio of 2/1, as shown in figure 4.
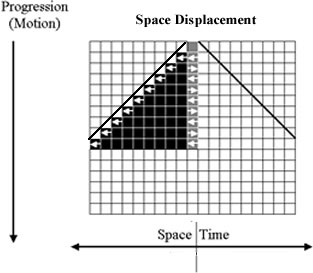
Figure 4. 2/1 Space Displacement PA
Clearly, the progression of the reversing aspect still exists in this new state, it’s just that it is now confined to one unit of space, or one unit of time by the continuous “direction” reversals. This type of motion differs from the uniformly increasing motion of the 1/1 ratio shown in the PA of figure 2, which is simply a translational scalar motion, in that the “direction” reversals constitute a scalar oscillation of the space aspect of the motion, as opposed to the former uniform translational motion of the unit ratio. Also, it is clear that the magnitude of the new motion is one unit, or c, given the size of the natural units of space and time that we derived from the Rydberg frequency previously, since 1/2, or 2/1, interpreted operationally, are both equal to 1, although in different “directions.” Larson designates the 1/2 progression ratio as the negative magnitude, and the 2/1 progression ratio as the positive magnitude. In addition, it is helpful, in refering to the two magnitudes, to call the 1/2 ratio “space motion,” and the 2/1 ratio “time motion,” although this concept of time motion is nothing like the time motion of science fiction, where it indicates time travel, as if one could travel back along the time progression to a previous point. Time motion in the sense we will use it simply means motion that has space/time dimensions that are the inverse of the dimensions of velocity, or t/s.
With the SSB produced by the “direction” reversals in the progression of one or the other of the reciprocal aspects of motion, we see that unit motion is asymmetrical; that is, a positive or negative magnitude of scalar motion is one unit removed, in one “direction” or another, from the reference datum of unit progression in accordance with the integer number system. Obviously, all magnitudes greater than one in either “direction” of the integer line represent magnitudes comprised of multiples of these fundamental magnitudes. However, this mathematical characterization of the two states of scalar motion also needs a physical interpretation. This can be accomplished using a “world line” chart commonly used to illustrate the spacetime concepts of relativity theory. In these 2D charts, the 3D spatial coordinate position of a physical event is plotted on one axis, while the 1D “position” of time is plotted on a perpendicular axis. In our adaptation of this concept, we plot the scalar expansion of the space aspect of the progression on one axis, and the scalar expansion of the time aspect on the other. Hence, the reference datum of the 1/1 space/time ratio is plotted as the 45 degree diagonal between them, and represents c speed. With space progression plotted horizontally along the x axis, and time progression plotted vertically along the y axis, as shown in figure 5, speeds below unit speed, c, are in the area above the diagonal, while speeds above c speed are located in the area below the diagonal.
Of course, speeds above c speed are not recognized in the LST, but remember, in the RST, these speeds are not space motion, s/t, but are time motion, t/s. Therefore, an RST entity, such as the 1/2 magnitude, with space/time dimensions s/t = 1/2, would be plotted above the unit line, while the inverse entity, with space/time dimensions t/s = 1/2, would be plotted below the unit line. Since, the space motion entity, s/t = 1/2, is confined to one space unit, while time progresses normally, it only increases in the increasing time “direction,” as indicated by the vertical red arrow next to the circled S in the diagram. Conversely, the time motion entity, s/t = 2/1 (t/s = 1/2), is confined to one unit of time, while space progresses normally, therefore it only increases in the increasing space “direction,” as indicated by the horizontal blue arrow next to the circled T in the diagram.
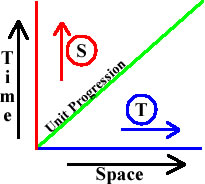
Figure 5. The RST World line Chart
In summary, then, on the strength of the SSB principle, the perfect symmetry of the uniform progression is “spontaneously” broken two ways by “direction” reversals that occur in the uniform progression patterns of either the space aspect or the time aspect of the space/time progression. When the reversals occur at some point in the space aspect of the unit ratio, a unit magnitude, 1/2 = 1, of space motion results that is composed of a scalar motion oscillating within one unit of space over time, ds/dt. Conversely, when the reversals occur at some point in the time aspect of the unit ratio, a unit magnitude, 2/1 = 1, of time motion results that is composed of a scalar motion oscillating within one unit of time over space, dt/ds. The mathematical relationships of these states is shown in the PA diagrams of figures 2-4, while the physical relationships are illustrated in the world line chart of figure 5.
Eventually, we will explore how these units can be combined to form theoretical entities that we can compare to observed physical entities, and how their properties may be calculated. We will also see how the arbitrary units of the LST can be converted into the natural units thus derived in the RST, and how doing so explains the constants of nature and eliminates them, when the physical dimensions of various properties and relationships between them are expressed in natural units of space and time.
Ok, now we have seen how that the perfect symmetry of the Reciprocal System’s initial state, the space/time ratio equal to a 1/1 progression, is the natural reference system of motion, the physical “zero” of the system, from which all physical activity is measured in the RST, and we used the PA in figure 2 above to generate this state of scalar motion as the unit progression ratio of space/time. Then we’ve seen how the symmetry of the initial state is spontaneously broken by “direction” reversals in the uniform progression of the space or time aspects of the motion, producing a second state of the system that deviates from the natural reference system by one unit in one of two possible “directions,” one of which is designated “negative” and the other “positive.” We used the PAs in figures 3 and 4 to generate these two progression ratios. We’ve also seen how generating these two possibilities of unit magnitude on either side of the unit ratio corresponds exactly to the initial three numbers of the integer number system, generated by the operational interpretation of magnitude that the rational number system generates. In fact, we can easily summarize all this information with just a few numbers:
1/2, 1/1, 2/1 = -1, 0, 1
Of course, mathematically speaking, any number in the integer number system can be obtained as a combination of these three numbers, from the number 2 to infinity in both “directions.” However, physically speaking, this would be quite cumbersome for very large numbers, and, intuitively, one would think, quite limited, and, actually, Larson realized that there is another possibility, another state of the system, a third state, although he didn’t use this terminology, and he didn’t know about the PAs, or use a worldline chart to explain these things. However, it turns out that the third state results when the two possibilities of the second state are combined; that is, a new progression ratio is generated by combining the progression ratios in the PAs in figures 3 and 4. This third state breaks the symmetry of the second state in a way that alters the pattern of the “direction” reversals, changing it from a continuous pattern of reversals to a periodic pattern of reversals, as shown in figure 6.

Figure 6. Periodic Reversal Progression Ratio
For the moment, we will skip the details of how the third state results from the combination of the two possible second states. However, we can see from the PA in figure 6 that the pattern of the progression ratio now consists of a series of two “direction” reversing units, repeated over and over again, separated by a non-reversing unit; that is, in this instance, the “direction” of the space progression reverses in progression unit 2 of row two, from increasing to decreasing, in unit 3 of row three, from decreasing to increasing, but, then, in unit 4 of row four, no “direction” reversal occurs. In unit 5 of row five, the “direction” reversals commence again, and the same pattern is then repeated, ad infinitum. The resulting space/time progression ratio of this pattern is s/t = 2/3, since, for every three units of time progression, there are two units of space progression, as can be verified in the PA of figure 6, by counting the the left pointing arrows accumulated on the space side that correspond to the accumulation of three right pointing arrows on the time side of the diagram at unit 4 of row four of the progression. This pattern is repeated every three units of progression from row four on, so that at row seven, the total accumulated space/time ratio is 4/6, at row 10, it is 6/9, and so on, maintaining a constant space/time progression ratio of s/t = 2/3.
Notice, however, that the operationally defined magnitude of the space/time progression ratio 2/3 is equal to 1, as is its inverse 3/2. Thus, the third state, a combination of the two possible forms of the second state, also has two “directions” of magnitude, one negative, the time displaced unit, and one positive, the space displaced unit, as shown in figures 7 and 8.

Figure 7. Unit Periodic Time Displacement

Figure 8. Unit Periodic Space Displacement
However, we can see that mathematically, when we combine the second state progression ratios, 1/2 and 2/1, we get
1/2 + 2/1 = 2/2 = 1/1,
but, even though mathematically the magnitude of the ratio of 2/2 is the same as the ratio of 1/1, namely 1, we know from the worldline chart of figure 5, that, physically, combining these two unit progression ratios is more than a mathematical operation; that is, it’s a physical operation as well. Indeed, it’s a combination of the S and T units of figure 5, and we know that the S unit is confined in space, but progressing in time, while the T unit is confined in time, but progressing in space. Therefore, the space/time relationship between them is unit space/time, or c speed. Hence, the possibility exists that the progression of space could bring a T unit into contact with an S unit, while the progression of time could bring an S unit into contact with a T unit. Significantly, however, in combination these units form an S|T unit that retains the characteristics of its constituent components; that is, the oscillating unit of space and the oscillating unit of time form an oscillating unit of space/time that progresses in both space and time, the same general characteristics of the physically observed photon. We can depict this combination on our worldline chart as shown in figure 9.

Figure 9. Physical Combination of S and T Units
Interestingly, the magnitude of the initial S|T unit can be increased in both “directions,” by adding S or T units indefinitly; that is, the 2/3 = 1 ST unit, plus an S unit, 1/2, equals a 3/5 = -2 S|T unit, while the 3/2 = 1 S|T unit, plus a T unit, 2/1, equals a 5/3 = 2 S|T unit. Hence, once again, we see the integer number system emerging from the rational number system, only now the rational number, the S|T unit of the periodic PA, is a complex number in the sense that it contains three ratios simultaneously - the 2/3 and 3/2 ratio and the 2/2 ratio. Hence, mathematically, the initial S|T unit forms the integer sequence
1/2, 1/1, 2/1 = -1, 0 , 1,
which can be extended in both “directions” infinitely, by the addition of S and T units to the combination.
…2/4, 1/2, 1/1, 2/1, 4/2… = …-2, -1, 0 , 1, 2…
In a future article, we will see how this reciprocal system of mathematics explains some amazing things about n-dimensional numbers and, consequently, how corresponding magnitudes of scalar motion are promising candidates to explain observed physical values of standard model entities. However, it’s important to note that Larson did not understand that the physical principle of reciprocity that is the foundation of the RST also may be applied to powerful effect in mathematics. Indeed, his Reciprocal System theory (RSt), contained in his work The Structure of the Physical Universe, the first reciprocal system theory to be constructed under the RST, and the first and only general physical theory of the universe ever developed, does not take advantage of these mathematical discoveries, which have only recently been discovered, more than a decade after his decease.
References:
1) David Hestenes, “New Foundations for Classical Mechanics, Second Edition,” Kluwer Academic Publishers, 1986.
2) Dewey B. Larson, “The Structure of the Physical Universe, Revised and Enlarged Edition, in Three Volumes,” North Pacific Publishers, 1979.
3) Lee Smolin, “The Case for Background Independence,”
http://arxiv.org/abs/hep-th/0507235.
4) Thomas Kuhn, “Structure of Scientific Revolutions,”
http://www.des.emory.edu/mfp/Kuhn.html
5) David Gross, “Viewpoints on String Theory,” NOVA,
http://www.pbs.org/wgbh/nova/elegant/view-gross.html
6) David Gross, “Gauge Theory- Past, Present, Future?”
http://www.psroc.phys.ntu.edu.tw/cjp/v30/955.pdf
7) David Gross, “The Role of Symmetry in Fundamental Physics,”
http://www.pnas.org/cgi/content/full/93/25/14256
8) Frank Wilczek and Betsy Devine, “Longing for the Harmonies,” W.W. Norton, 1989.
9) Sean Carroll, “Minus Numbers,” preposterousuniverse blog,
http://cosmicvariance.com/2005/08/03/minus-numbers/#comments
10) Jon Hays, “Arithmetic Redux”,
http://members.fortunecity.com/jonhays/redux.htm
11) Merriam-Webster Online, “zero,”
http://www.m-w.com/dictionary/zero
12) Steven Wolfram, “Mathworld at Wolfram Research,” http://mathworld.wolfram.com/ElementaryCellularAutomaton.html
(See also: Larson’s New System of Physical Theory - Part I - Larson’s New System of Physical Theory - Part II - Larson’s New System of Physical Theory - Part III - Larson’s New System of Physical Theory - Part IV)