Fourth Post in the BAUT RST Forum
The fourth post in the BAUT forum follows. These posts are a continuation of the RST thread in the “Against the Mainstream” forum of BAUT.
+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
Larson proceeded to develop his scalar motion theory from the basic postulates of the RST, without the benefit of Hestenes’ work. Therefore, the concepts of duality and dimension, and how they are related to each other, as revealed in the binomial expansion, and the concepts of Clifford algebra that encapsulate these ideas in terms of n-dimensional numbers, though they were certainly available to informed specialists in the field of mathematics, during Larson’s time, they were scarcely visible to many uninformed specialists, let alone non-specialists. They didn’t become generally known until Hestenes’ efforts to use them as the basis for a new, unified, language of physics, began to gather steam in the eighties and nineties.
Today, we know that the purpose of GA, according to Hestenes, is to facilitate physics educational and research efforts. In delivering his 2002 Oersted Medal Lecture, “Reforming the Mathematical Language of Physics,” Hestenes told the audience:
| The generic name for that language is Geometric Algebra (GA). My purpose here is to explain how GA simplifies and clarifies the structure of physics, and thereby convince you of its immense implications for physics instruction at all grade levels. I expound it here in sufficient detail to be useful in instruction and research and to provide an entre to the published literature. |
- GA seamlessly integrates the properties of vectors and complex numbers to enable a completely coordinate-free treatment of 2D physics.
- GA articulates seamlessly with standard vector algebra to enable easy contact with standard literature and mathematical methods.
- GA Reduces “grad, div, curl and all that” to a single vector derivative that, among other things, combines the standard set of four Maxwell equations into a single equation and provides new methods to solve it.
- The GA formulation of spinors facilitates the treatment of rotations and rotational dynamics in both classical and quantum mechanics without coordinates or matrices.
- GA provides fresh insights into the geometric structure of quantum mechanics with implications for its physical interpretation. All of this generalizes smoothly to a completely coordinate-free language for spacetime physics and general relativity to be introduced in subsequent papers.
However, what few people knew, or could have even cared about at the time, was how the language that simplifies and clarifies the structure of vectorial physics, would also illuminate the work of Larson eventually. Indeed, its contribution to the science of scalar physics, may eventually prove to be more valuable to science in general than its contribution to the science of vector physics, since physicists and educators, well trained in the traditional language of vector and complex algebra, are relunctant to replace the known and familiar language of physics, with an unknown and unfamiliar one.
It may seem ironic that a new system of vector algebra, designed to improve the existing mathematical language of the mature science of vector physics, ends up providing a new mathematical language for the immature science of scalar physics. Yet, it is easy to understand it, when one looks at GA, not as a geometric algebra, but as a multi-dimensional number system that contains, as an integrated whole, advanced concepts of number that correspond to both scalar and vector magnitudes.
In starting our discussion of this expanded view of GA, it’s important to recognize that there is a pleasing, but mysterious, symmetry in the grouping of its n-dimensional basis numbers: 1 + 3 + 3 + 1 = 8, which seem to pair vectors and bivectors (3+3), and scalars and trivectors (1+1). When we interpret this mathematical symmetry geometrically, as the 2x2x2 cube, with the scalar basis point at the intersection of the three orthogonal basis vectors and the three orthogonal basis bivectors, a point which coincides with the center of the eight corners of the pseudoscalar basis trivector, the physical beauty in the symmetry of its form, the conceptual beauty in the symmetry of its algebra, and the intellectual beauty in its complete and flawless union of the meanings of direction, duality, and dimension, is simply startling in its power to make one marvel.
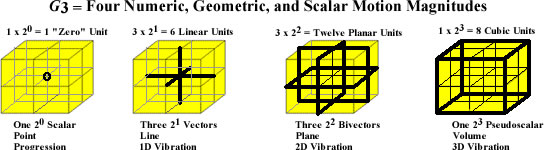
Figure 1. Larson’s Cube
I’ve dubbed it “Larson’s Cube,” because he initially used it to illustrate the eight units of three-dimensional scalar motion in the RST, but, now, when I look at it, it’s as if I see the physical, mathematical, and intellectual structure of the entire universe contained in its simple, three-dimensional, figure. It seems to me to contain the great secret of nature’s unity, as it were, the secret to how she unifies the continuum and the quantum, the secret that is the Holy Grail of theoretical physics.
Of course, I can’t prove these things yet, but I’m so convinced of their veracity that I have organized and incorporated the “Dewey B. Larson Memorial Research Center,” or “Larson Research Center,” for short, to employ the mathematicians, physicists, and other professionals who can perform the scientific work necessary to prove it, to the extent that it may be possible to do so.
The reason that I see so much beauty in this cube is that it seems to contain every element that is necessary for a theory of everything, but nothing more. It integrates the concepts of motion, mathematics, and geometry into one graphic, which can be viewed as a single expression of that motion, which in the RST, we assume is the one component of which the universe consists. To see it expressed in one graphic, is tantamount to looking at the very foundation of the universe, in all its awesome power.
Clearly, however, I’m getting ahead of myself. To understand the power of Larson’s Cube, we have to understand how it integrates the science of vectorial motion, with the science of scalar motion, and it all begins with the power of one, but not the quantitative interpretation of the number one, but the operational interpretation (OI) of the rational numbers as one.
As the ancient Greeks understood it, the number one (monad) represents eternity, and they probably learned it from the Egyptians, who in turn probably learned it from the Hebrews. In our OI number one, 1/1, we can understand this as signifying infinity/infinity is equal to 1/1; in other words, the number one contains all the numbers, 1/1, 2/2, 3/3, …n/n, where n goes to infinity.
Normally, this fact is regarded as trivial, until, that is, we realize that this unity, apeiron, to the ancient Greeks, is a principle of reality that subsumes (i.e. contains, encompasses) peiron, or that which is limited, bounded, finite. These are the notions of continuum and quantum, the very notions that are plaguing theoretical physics. Larson’s RST necessarily begins with this unity, which he calls the “unit progression” of space and time, as the initial condition of the universe of motion, because he defines space as the reciprocal of time, as motion, and motion as the sole component of the universe.
However, in describing the ancient Greek idea of this, we read in Wikipedia:
| When the apeiron is inhaled by the peiron it causes separation, which also apparently means that it “separates and distinguishes the successive terms in a series.” Instead of an undifferentiated whole we have a living whole of inter-connected parts separated by “void” between them. This inhalation of the apeiron is also what makes the world mathematical, not just possible to describe using math, but truly mathematical since it shows numbers and reality to be upheld by the same principle: both the continuum of numbers (that is yet a series of successive terms, separated by void) and the field of reality, the cosmos - both are a play of emptiness and form, apeiron and peiron. |
| …I decided to undertake the task of devising a method whereby the magnitudes of certain physical properties could be calculated from the chemical composition…As might be expected, the task that I had undertaken was a long and difficult one, but after about twenty years I had arrived at some interesting mathematical expressions in several areas, one of the most intriguing of which was an expression for the inter-atomic distance in the solid state in terms of three variables clearly related to the properties portrayed by the periodic table of the elements. But a mathematical expression, however accurate it may be, has only a limited value in itself. Before we can make full use of the relationship that it expresses, we must know something as to its meaning. So my next objective was to find out why the mathematics took this particular form. I studied these expressions from all angles, analyzing the different terms, and investigating all of the hypotheses as to their origin that I could think of. This was a rather discouraging phase of the project, as for a long time I seemed to be merely spinning my wheels and getting nowhere. On several occasions I decided to abandon the entire project, but in each case, after several months of inactivity I thought of some other possibility that seemed worth investigating, and I returned to the task. Eventually it occurred to me that, when expressed in one particular form, the mathematical relation that I had formulated for the inter-atomic distance would have a simple and logical explanation if I merely assumed that there is a general reciprocal relation between space and time. |
| My first reaction to this thought was the same as that of a great many others. The idea of the reciprocal of space, I said to myself, is absurd. One might as well talk of the reciprocal of a pail of water, or the reciprocal of a fencepost. But on further consideration I could see that the idea is not so absurd after all. The only relation between space and time of which we have any actual knowledge is motion, and in motion space and time do have a reciprocal relation. If one airplane travels twice as fast as another, it makes no difference whether we say that it travels twice as far in the same time, or that it travels the same distance in half the time. This is not necessarily a general reciprocal relation, but the fact that it is a reciprocal relation gives the idea of a general relation a considerable degree of plausibility. |
| So I took the next step, and started considering what the consequences of a reciprocal relation of this nature might be. Much to my surprise, it was immediately obvious that such a relation leads directly to simple and logical answers to no less than a half dozen problems of long standing in widely separated physical fields. |
According to the Wikipedia article, this same challence faced the ancients:
| What really sets this apart from Anaximander’s original ideas is that this play of apeiron and peiron must take place according to harmonia (harmony), about which Stobaeus commentated: “About nature and harmony this is the position. The being of the objects, being eternal, and nature itself admit of divine, not human, knowledge – except that it was not possible for any of the things that exist and are known by us to have come into being, without there existing the being of those things from which the universe was composed, the limited and the unlimited. And since these principles existed being neither alike nor of the same kind, it would have been impossible for them to be ordered into a universe if harmony had not supervened – in whatever manner this came into being. Things that were alike and of the same kind had no need of harmony, but those that were unlike and not of the same kind and of unequal order – it was necessary for such things to have been locked together by harmony, if they are to be held together in an ordered universe.” A musical scale presupposes an unlimited continuum of pitches, which must be limited in some way in order for a scale to arise. The crucial point is that not just any set of limiters will do. We cannot just pick pitches at random along the continuum and produce a scale that will be musically pleasing…In Philolaus’ terms the fitting together of limiters and unlimiteds involves their combination in accordance with ratios of numbers (harmony). Similarly the cosmos and the individual things in the cosmos do not arise by a chance combination of limiters and unlimiteds; the limiters and unlimiteds must be fitted together in a “pleasing” (harmonic) way in accordance with number for an order to arise. |
| The question that naturally arises at this point is, How can these displacements of the space-time ratio exist, when each unit of space is always equivalent to a unit of time? Inasmuch as the progression is scalar, the only variation that can take place is in the scalar direction: outward (positive) or inward (negative) …But…one of the components may alternate scalar directions, so that the negative progression of one unit of this component cancels the positive progression of the preceding unit. A series of such reversals thus results in the formation of a multiple unit of motion in which n units of space (or time) are associated with only one unit of time (or space). |
Reader Comments