The Larson Research Center

In the previous entries below, we’ve discussed the concept of number, not as increasing/diminishing magnitude, but as order in progression, introducing an index of space|time progression, P_n, which we used to define a new set of natural, reciprocal, numbers, as a nested set of ordered sets:

{P₁}; {{P₁} {P₂}}; {{P₁} {P₂} {P₃}}; … {{P₁} {P₂} {P₃}…{PN₂}}

Next, we substituted these reciprocal numbers for the natural numbers of the tetraktys, showing how they provide a scalar version of what is normally interpreted as a vector (i.e. geometric) version of the binomial expansion. We did this on the basis of our identification of the binomial characteristic of the tetraktys, with the duality of vector direction, reasoning that the dual concept of scalar “direction” would provide a similar (isomorphic, or analogous) result, provided that we could find a way to define orthogonality in scalar terms.

Fortunately, it can be shown that the concept of scalar orthogonality, or independence of a combination of scalar values, is inherent in the combination of S|T units, as the preons of standard model entities, called S|T triplets, where the A, B, C, nodes of the triplets are independent reciprocal numbers. Thus, the scalar version of the tetraktys can be constructed, using the set of natural, reciprocal, numbers: 

(1/1)⁰

(2/2)⁰ (2/2)¹  

(4/4)⁰ {(2/2)¹ (2/2)¹} (2/2)²

(8/8)⁰ {(2/2)¹ (2/2)¹ (2/2)¹} {(2/2)² (2/2)² (2/2)²} (2/2)³

where the differences in the exponents are indices of dimensional symmetry; For instance, because 2/2 = 1/1 + 1/1, a one-dimensional degree of freedom is attained at P₂ = (2/2)⁰, relative to the “directions” at P₁ = (1/1)⁰, which are realizable as 1/2 or 2/1, representing two scalar “directions” analogous to the two vector directions of one-dimensional lines.

Similarly, at P₄ = P₂ + P₂, a two-dimensional symmetry is attained, since the product of P₂ with itself is (P₂)² (i.e. (2/2)*(2/2) = (2/2)² = (4/4). Likewise, at P₈, a three-dimensional symmetry is attained (2/2)*(2/2)*(2/2) = (2/2)³ = (8/8).

Thus, what we have in the scalar tetraktys is a binomial expansion of scalar “direction,” analogous to the binomial expansion of vector direction, and since the elements of the vector tetraktys can be regarded as the linear spaces, constituting the multivectors of GA, it is reasonable to conclude that a scalar algebra can be constructed over the linear spaces of the scalar tetraktys, as well.

With this much understood, however, it is recognized that there is a long way to go yet. In constructing GA, the first step is to define the geometric product, as consisting of the combination of the inner and outer product, where the inner product is a scalar, and the outer product is a vector (now called a bivector), and in this way describing the magnitude, or length, (inner product) and direction (outer product) of any vector in three spatial dimensions. This is very advantageous in GA, because the concept of vector is easily incorporated to express the complementary relation of kinetic and potential energy, or torque and work, or B field and E field, etc. in vectorial physics.

Of course, this was all accomplished without the benefit of GA, before it was uncovered by Hestenes. However, it was accomplished by means of what turned out to be subalgebras of GA, in the form of Gibbs’ vector algebra, and in the form of quaternions, disguised as matrices, and in the form of complex numbers, which are all subsumed by GA. Consequently, since the belated advent of GA, many physics applications have been rewritten in this language, applying it, not because the solutions were needed in any practical sense, but because they enable the central ideas and concepts of physics to be given a more intuitive, geometrical, interpretation, one which is much simpler and concise. 

We recognize this as a very propitious development for us here at the LRC, if we can use these applications, and the GA language used to describe them, to gain the crucial insight needed for the development of a scalar algebra (SA), suitable for doing physical calculations in RST theory.

The fact that Hestenes develops GA step by step in his book New Foundations for Classical Mechanics makes it the natural choice for our guide, but the fact that GA is a fomulation based on axioms, whereas our development can have no axioms, defines the biggest challenge in this approach. We first have to understand what the axioms are and how, and why, they do what they do in GA, before we can hope to see the way forward. That these axioms have to do with the operations, or the meaning, of multiplication and addition, in terms of one-dimensional vectors, bivectors, composed of vectors, and trivectors, composed of vectors and bivectors, while we have no vectors, bivectors, or trivectors, just scalars, and at the same time have discovered a definite and important meaning of addition, multiplication and division, in terms of our scalars, gives us a sense of the challenge: It is daunting.

To help us, it will be desirable to relate the scalar tetraktys to a scalar version of “geometry;” that is, we want to have a visual concept of the scalar analogs to 3D geometric entities, points, lines, areas, and volumes, as they relate to each other in the form of multi-dimensional, reciprocal, numbers. Of course, to do this, we return once again to Larson’s cube. This cube is called Larson’s cube, because he used it, in the course of defining scalar magnitudes, to show why the pseudoscalar has 2³ = 8 units of scalar magnitude, in a 3D system, not six, as some were want to argue. In chapter 12 of Nothing But Motion, he writes:

In three-dimensional space (or time) there can be two displacement units in each of the three dimensions, and the maximum three-dimensional unidirectional displacement is therefore 2³, or 8, units.

There have been some suggestions that the number of possible directions (and consequently displacements) in three-dimensional space ought to be 3 x 2 = 6 rather than 2³ = 8. It should therefore be emphasized that we are not dealing with three individual dimensions of motion, we are dealing with three-dimensional motion. The possible directions in a three-dimensional continuum can be visualized by regarding a two-unit cube as being an assemblage of eight one-unit cubes. The diagonals from the center of the assemblage to the opposite corner of each of the cubes then define the eight possible directions.

The cube, with its eight directions, as described by Larson, is illustrated below.

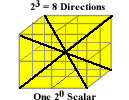
Figure 1. Larson’s Cube

Mapping the vector tetraktys to this cube, we can easily identify its multidimensional linear spaces with the geometric components of the stack of eight cubes, as illustrated in figure 2 below.

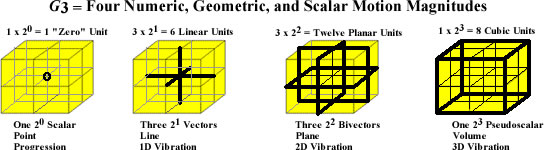
Figure 2. The Eight Dimensions of the Vector Tetraktys (1331) Mapped to Larson’s 2x2x2 Cube

The graphic in figure 2 was constructed several years ago and the text indicates our preliminary attempt to identify scalar magnitudes with vectorial magnitudes, but this attempt was premature and naive, so the reference to these concepts in figure 2 should be ignored. However, the figure does show how the linear spaces of G3, in GA, can be mapped to Larson’s cube. The first space contains 1 type of entity, the 0D scalars, analogous to a single geometric point, and is located at the center intersection of the 8 cube assembly. The second space contains 3 types of entities, the 1D vectors, analogous to three, independent (i.e. orthogonal), geometric lines, and is identified as the intersection of the horizontal and vertical edges of the eight cubes in the assembly. The third space also contains 3 types of entities, the 2D bivectors, analogous to three, independent (i.e. orthogonal), geometric planes, and is identified as the interface of the horizontal and vertical planes of the eight cubes. Finally, the fourth space contains 1 type of entity, the single 3D trivector, analogous to a unit cube, and is identified by the twelve outside edges of the assembly, forming its eight corners.

This geometric view of the vector tetraktys is helpful in mapping the scalar tetraktys as well, even though the “directions” of the scalar values have no geometric meaning; that is, the directions of vector distance magnitudes, and the associated directed numbers of GA, are isomorphic to the “directions” of scalar magnitudes, and the “directed” numbers of a future SA, but they are not identical. We might say that the geometric representation of the scalar tetraktys is symbolic of the scalar spaces in SA. In the graphic of figure 3 below, the scalar “directions” are indicated by colors, corresponding to the geometric directions of the cube, but the text of the graphic, referring to vibrations, is still erroneous and should be ignored.

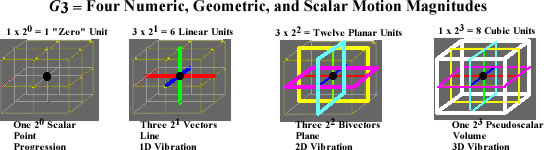
Figure 3. The Eight Dimensions of the Scalar Tetraktys (1331) Mapped to Larson’s 2x2x2 Cube

In this graphic, only the edges of the 2D and 3D magnitudes are colored for greater visibility, but the combinations follow the scalar concept faithfully, except, of course, in reality colors are mixed to obtain the “higher dimensional” color, not multiplied (actually, it amounts to the same thing, when you think about it - more on this later). Yet, the color black, in the scalar space, located at the origin of the cube, as a 0D scalar point, and the 1D primary colors, combining to form the 2D secondary colors, and these, combining together, or each in turn, with the “odd man out” primary, to form the 3D white color of the pseudoscalar, correspond perfectly to the linear spaces of GA, where

a; a,b,c; a^b, a^c, b^c; a^b^c

symbolize the k-blades of each linear space. It should be noted, however, that in our color scheme, the pattern of each color, denoting an independent dimension, should be altered to distinguish the polarities, or two “directions” above and below unity. In this way a striped color, for instance, could be used to indicate the opposite scalar “direction” indicated by the same, solid, color. This will be attempted when the image is updated later.

The important point is to recognize that the magnitude and direction of scalars, vectors, bivectors, and trivectors, in the vector tetraktys, are defined algebraically in GA, to provide an algebraic language, which is used to describe the magnitude and direction of multiple, one-dimensional, vectors, in the three-dimensional space of the cube. This is done, by defining a unit basis for each element of the space, and treating these as a righthanded, or dextral, set of basis vectors, interpreting the cube as a whole, with a bottom corner selected as the origin.

As Hestenes shows, scalar addition and multiplication are easily defined in this vector space, as is scalar multiplication of a vector. But scalar addition with a vector, an anathema to traditional approaches, is also defined, and is, in fact, the central feature of GA. In our case, however, we are not concerned with the magnitude and orientation of a combination of 1D vectors in a 3D space. Instead, we are interested in the configuration, we might say, or in the linear combination of the multi-dimensional components of the scalar tetraktys. This makes the location of the scalar space at the origin of the cube critical, for our purposes, because it preserves the proper tetraktys relation, between the scalar and the pseudoscalar, as reciprocal entities, in the algebra.

For instance, when the point at the center grows (“scales”), from (1/1)⁰ to (8/8)⁰, the cube becomes fully “populated” we might say, but when the scalar point is reduced from (8/8)⁰ to (1/1)⁰, for any reason, the cube is “depopulated.” Of course, the intermediate values play an important role as well. The objective seems to be to determine how these values might change, and what are the rules governing the changes. We already know that the periodic table can be generated by this process, so we are highly encouraged to pursue its investigation.