The Larson Research Center

Well, we finished up the LRC Seminar in American Fork last night.  I’d been working on the presentation all week. It was entitled, “LRC Science, What is it? Part II.”  In the first part, on the 15th of November, I tried to establish the rationale for asserting that the LRC science is scalar science, as opposed to vector science, but, in spite of my best effort, I didn’t think I carried the day with the “docs.”  They’re not an easy crowd to convince, but then that’s good.

This time I had more ammunition.  It’s a new chart I’ve designed to show that the four numbers of the tetraktys are actually four dimensions of motion.  We talked about how, from the ancient Greeks, to modern times, the focus of science has been on this mysterious and enchanting collection of numbers. I’ve already discussed the new chart in the New Math blog, but I’ll insert it here too, in figure 1 below. I’ve thought since last night, that, given that each dimension of motion is a number raised to a power, the word dimension in this connection might be confusing. So, I’ll refer to them as bases of motion, instead of dimensions.  Each base of motion is raised to a power of magnitude.

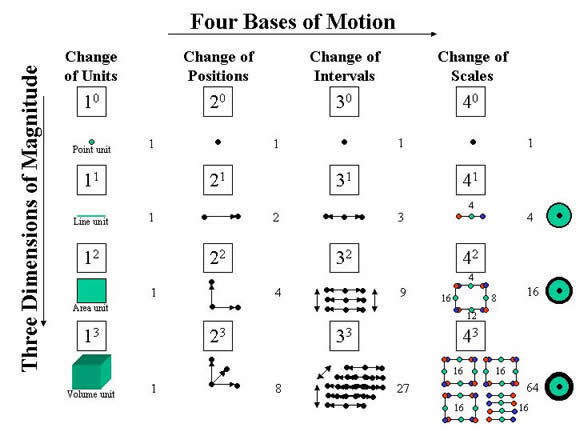
Figure 1. Four Bases of Motion 

Each base of motion is a fundamentally different way to represent a change of space over time (velocity), or a change of time over space (energy).  The second base defines the units of the first base, by a change of space (time) position, the third by a change of space (time) interval, and the fourth by a change of space (time) scale.  Our discussion of this chart last night focused on how the legacy scientists are trying to exploit the principle of rotation symmetry to explain all natural phenomena, but here we see that rotation is not necessarily the appropriate principle to use, since it applies to the second base of motion (base 2 motion), or the familiar vector motion of position change in space.

Of course, the base 2 motion and the base 3 motion are a familiar part of LST physics, and they have been thoroughly studied, but the base 4 motion, scalar motion, is not even recognized by LST scientists. Consequently, the most relevant question asked last night was, naturally enough, “What is it that is conserved in base 4 motion?”  However, even though this is the first question one would expect of a physicist, I had to stop and think about it.  My first thought was, well, in a universe of nothing but motion, the thing conserved has to be motion, and I said so, but I’ve never heard of a law of motion conservation.  We are all familiar with the conservation laws of momentum and energy, but a conservation law of velocity?  How is velocity conserved? It started me thinking.

But before I start explaining what those thoughts were, notice how the chart shows n-dimensional magnitude as space magnitude. This is because dsⁿ/dtⁿ is a measure of space magnitude in our experience, but what about the dtⁿ/dsⁿ magnitudes? Obviously, the same principles of three dimensions of magnitude for each base of dt/ds motion hold, but then the magnitudes become magnitudes of time, as if we were looking at linear, square, and cubic dimensions of time magnitude!

Of course, we’ve been doing this all along in the equations, only we call the n-dimensional time magnitudes different names and think of them as scalars, not time vectors. Obviously, the names of these three time scalars are energy (dt/ds), momentum (dt²/ds²), and mass (dt³/ds³), but they correspond to the line (ds/dt), area (ds²/dt²), and volume (ds³/dt³) space magnitudes in the chart above. Moreover, there’s another disconnect too, because we aren’t accustomed to thinking of linear, square, and cubic units of motion either, even though these are clearly what the chart implies.

However, it becomes clear what is happening when we recognize that time has no direction in space, and space has no direction in time; that is, the dimension of time in our velocity equations is scalar (n⁰), regardless of the dimension of the motion.  Also, In base 2 motion, all change of space is linear change, otherwise the object changing position would grow in one, or in the other, or in both, of the remaining two dimensions. So, the two-dimensional base 2 motion, ds₂²/dt₂², is interpreted as two space vectors, or V₁ = ds/dt x V₂ = ds/dt, and we use the cross product in vector algebra to obtain the resultant vector, ds/dt, or the dot product to get the scalar, which, being complements of one another, vary depending on the orthogonality of the vectors. 

Nevertheless, in the case of GA, the inner product and the outer product are combined, into the geometric product, to calculate a 2D area defined by the angle of the vectors, like someone drawing a two-dimensional space, by rotating one vector into a second dimension relative to the other.  Thus, GA defines a 2D magnitude through a 1D rotation, which is related to the 1D magnitude of the resultant vector of vector algebra, only different:  One is a magnitude of motion, the result of forces in different directions, while the other is an unspecified magnitude of higher dimension, usually thought of as a magnitude of space.  Why is this?  Because, as Newton said, geometry has nothing to say about how the “right lines and circles” of geometry are drawn.  These are determined by “principles brought from without,” the principles of mechanics.

But now we see that there are several principles of mechanics at play here.  As a matter of fact there are three such principles, and any one of them can produce the magnitudes of geometry, but not all in the same manner.  Change of position motion is one way, but it is not the only way to do it.  Change of interval, and change of scale will also do it.  What confuses our understanding of what is going on is the incorrect notion that n-dimensional magnitudes are magnitudes of space, when in reality, they are only magnitudes of motion with two, reciprocal aspects, space and time.

The proof of this is in the recognition that neither space or time can be measured independently.  Only motion can be measured.  We can measure past, or future, motion that changed, or will change, the positions of objects, by repeating the original motion, but disregarding the magnitude of the time or space aspect of it, in order to get the reciprocal aspect of it that we want.  For example, we can repeat the original motion that separated two objects, by moving a measuring rod between the two positions of interest and reading how many space units are required to span the distance, regardless of the time it takes to move the rod into place.  Thus, the speed may not be the same as the original motion separating the two objects, but the motion of the rod has shown us what the magnitude of the space aspect of that motion must be, regardless of the time aspect.

We call this measured distance between the two objects “space,” but it doesn’t exist as something independent of the motion between the objects.  It certainly is not something that exists between these two locations that can be curved, warped, or vibrated, for instance.  Such an idea is absurd. Thus, the motion between the positions of objects, or the area underneath or above, to the right of, or to the left of, or in front of, or behind the position of a plane of objects, or the volume within a cube, or sphere, of objects in different positions, is a representation of the linear, quadratic, or cubic magnitude of past motion that separated the objects, and nothing else.

Furthermore, it doesn’t matter whether the past motion was base 2, 3, or 4 motion.  In fact, there’s no way to tell the difference in most cases, and this thought brings me to the point I wanted to explain, about the idea of conservation of velocity, but I’ll have to wait until next time to relate my thoughts on that.  The only point that I need to make now is that, by interpreting velocity equations as magnitudes of motion, we need to recognize that these magnitudes can be n-dimensional, as the chart shows, not just one-dimensional, as in the vectors of base 2 motion.  For instance, two or three dimensions of time in a velocity equation, can be interpreted as the time aspect of two or three-dimensional magnitudes of motion, as well as the second, or third derivative, of one-dimensional motion.