Deriving Physical Units From Fundamental Units of Measure
In the previous post, I discussed how, in the LST system of vectorial science, energy is defined as a scalar quantity, even though it has the space/time dimensions of inverse velocity, which is considered a vector (magnitude with direction), in vectorial science. We found that the key to understanding this enigma is the recognition that vectorial energy is defined as a vectorial displacement from unity. If the direction of a force vector neither veers to the left or to the right of a center line (the inner product is unity), it creates no displacement to the left or right of center, but, if it bears to the right or left of center, like the pointer on an amp meter, such displacement is regarded as positive or negative work, which is a manifestation of positive or negative energy.
The analogy to the time or space displacement of the unit scalar progression, leading to the SUDR or TUDR, is inescapable, and this gives us a clear picture of the relation of velocity (ds/dt) and energy (dt/ds), as inverse ratios of space and time. This also gives us a clearer understanding of the vectorial system of science vis-a-vis the scalar system of science. Vectorial concepts are analogs of scalar concepts; that is, there is a scalar and vector way to understand space and time and velocity and energy, and the understanding of the one helps in our understanding of the other.
However, lacking the knowledge of scalar motion, vectorial science has to use space, time and mass to calibrate the units of the vectorial system, such as the centimeter-gram-second system (CGS), or the meter-kilogram-second system (MKS), or its modern version, the International System of Units (SI). Nevertheless, given the knowledge of the scalar system, it is clear that a calibration of space and time units suffices for defining all other physical units. Indeed, even without a knowlege of Larson’s scalar system of motion, the SI system of units can be redefined in terms of space and time, as shown by Engineer Saviour Borg of Blaze Labs. He has recognized that understanding the dimensions of physical quantities is paramount to unifying physical theory, and that, through the use of dimensional analysis in the study of the key relationships of physical quantities, we can gain great insight into the concepts that underly the fundamental principles of nature. He writes:
One of the most powerful mathematical tools in science is dimensional analysis. Dimensional analysis is often applied in different scientific fields to simplify a problem by reducing the number of variables to the smallest number of “essential” parameters. Systems which share these parameters are called similar and do not have to be studied separately. Most often then not, two apparently different systems are shown to obey the same laws and one of them can be considered to be analogous to the other.
The dimension of a physical quantity is the type of unit needed to express it. For instance, the dimension of a speed is distance/time and the dimension of a force is mass×distance/time². Conventionally, we know that in mechanics, every physical quantity can be expressed in terms of MLT dimensions, namely mass, length and time or alternatively in terms of MLF dimensions, namely mass, length and force. Depending on the problem, it may be advantageous to choose one or the other set of fundamental units. Every unit is a product of (possibly fractional) powers of the fundamental units, and the units form a group under multiplication.
However, the number of fundamental units of the SI system has been expanded, from the three of the MKS system, to seven fundamental units in the SI. Generally, the more the fundamental units required to define a system, the less fundamental the system is. Borg comments on this:
We know that measurements are the backbone of science. A lot of work has been done to get the present self-coherent SI system of physical parameters, so why not choose SI as the foundation of a unifying theory? Because if the present science is not leading to unification, it means that something in its foundations is really wrong, and where else to start searching if not in its measuring units. The present SI system of units have been laid out over the past couple of centuries while the same knowledge that generated them in the first place have changed (sic), making the SI system more or less a database of historical units. The major fault in the SI system can be easily seen in the relation diagram shown here, officially issued by BIPM (Bureau International des Poids et Mesures). We just added the 3 green arrows for the Kelvin unit. One would expect to see the seven base units totally isolated, with arrows pointing radially outwards towards derived units, instead, what we get is a totally different picture. Here we see that the seven SI base units are not even independent, but totally interdependent like a web, and so do not even strictly qualify as fundamental dimensions.
Borg permits use of his published materials, given due attribution and notification, so I have included the diagram he refers to in figure 1, below.

Figure 1. Borg’s Diagram of the “Fundamental Units” of SI
Borg explains how most of these units are redundant, some even included for historical reasons, but he has drawn the green arrows from mass, space and time to temperature, because temperature, in units of Joules, has the dimensions of energy. He writes:
Temperature can be seen as an alternative scale for measuring that characteristic energy [Boltzmann’s constant times temperature, which relates the energy portion of temperature to its units]. The Joule is equivalent to Kg/m2/sec2, so for the Kelvin unit we had to add the three green arrows pointing from Kg, metres and seconds which are the SI units defining energy.
Of course, we’ve been discussing the dimensions of energy as t3/s3 * s2/t2 = t/s, in Einstein’s equation, E = mc2, but Borg points out that, in the SI diagram, of all of the SI units, only two don’t have incoming arrows, showing their dependence upon other units. Hence, the only two, independent, units are the unit of mass and the unit of time. He writes:
How many dimensions can the SI system be reduced to? Looking again at the SI relations diagram, let us see which units DO NOT depend on others, that is which are those having only outgoing arrows and no incoming arrows. We see that in the SI system, only the units Seconds and Kg are independent. So, this means that the SI system can be reduced to no more than two dimensions, without losing any of its physical significance of all the involved units.
Yikes, does this mean that only mass and time are fundamental units? Borg explains:
But we know that there are a lot of other combinations that can lead to the same number of fundamental dimensions, and that Kg and Seconds might not be the most physically meaningful independent dimensions. Strictly speaking only Space and Time are fundamental dimensions …. so what are the rest? Just patches in physics covering our ignorance, our inability to accept that point particles, with the fictitious Kg dimension, do not exist.
Curiously, however, even though Borg recognizes that “only space and time are fundamental dimensions,” he doesn’t refer to the most important relation between space and time, indeed the only known relation of space and time, motion. Nevertheless, he proceeds to redefine the SI units, in terms of space and time only, as shown in figure 2 below.

Figure 2. Borg’s Diagram of the Redefined “Fundamental Units” of SI
Notice that the arrow from time to space in figure 1 has been removed in figure 2, apparently indicating that the space and time units are regarded as independent units, not as the two reciprocal aspects of one component. However, recognizing, as Larson did, that space is just the reciprocal of time, in the equation of motion, the diagram of the SI units in figure 2, above, can be redrawn, as in figure 3, below.
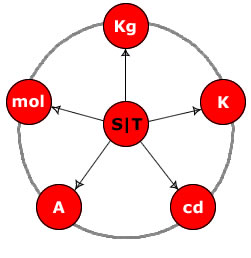
Figure 3. Fundamental Units of SI Based on Scalar Motion
Nevertheless, even though Borg doesn’t take the final step that Larson took, in concluding that scalar motion is the fundamental physical unit, he is still able to show how the space/time dimensions of the fundamental unit of motion can be used to derive all other physical units, as shown in table 1 below.
| Parameter | Units | SI units | ST Dimensions |
|---|---|---|---|
| Distance S | metres | m | S |
| Area A | metres square | m2 | S2 |
| Volume V | metres cubed | m3 | S3 |
| Time t | seconds | s | T |
| Speed/ Velocity u | metres/sec | m/s | ST-1 |
| Acceleration a | metres/sec2 | m/s2 | ST-2 |
| Force/ Drag F | Newtons | Kgm/s2 | TS-2 |
| Surface Tension g | Newton per meter | Kg/s2 | TS-3 |
| Energy/ Work E | Joules | Kgm2/s2 | TS-1 |
| Power P | Watts or J/sec | m2 Kg/s3 | S-1 |
| Density r | kg/m3 | kg/m3 | T3 S-6 |
| Mass m | Kilogram | Kg | T3 S-3 |
| Momentum p | Kg metres/sec | Kgm/s | T2 S-2 |
| Impulse J | Newton Seconds | Kg m/s | T2 S-2 |
| Moment m | Newton metres | m2 Kg/sec2 | T S-1 |
| Torque t | Foot Pounds or Nm | m2 Kg/sec2 | T S-1 |
| Angular Momentum L | Kg m2/s | Kg m2/s | T2 S-1 |
| Inertia I | Kilogram m2 | Kgm2 | T3 S-1 |
| Angular velocity/frequency w | Radians/sec | rad/sec | T-1 |
| Pressure/Stress P | Pascal or N/m2 | Kg/m/sec2 | T S-4 |
| Specific heat Capacity c | J/kG/K | m2/sec2/K | S3 T-3 |
| Specific Entropy | J/kG/K | m2/sec2/K | S3 T-3 |
| Resistance R | Ohms | m2Kg/sec3/Amp2 | T2 S-3 |
| Impedance Z | Ohms | m2Kg/sec3/Amp2 | T2 S-3 |
| Conductance S | Siemens or Amp/Volts | sec3 Amp2/Kg/m2 | S3 T-2 |
| Capacitance C | Farads | sec4Amp2/Kg/m2 | S3 T-1 |
| Inductance L | Henry | m2 Kg/sec2/Amp2 | T3 S-3 |
| Current I | Amps | Amp | S T-1 |
| Electric charge/flux q | Coulomb | Amp sec | S |
| Magnetic charge/flux f | Weber or Volts Sec | m2 Kg/sec2/Amp | T2 S-2 |
| Magnetic flux density B | Tesla /gauss/ Wb/m2 | Kg/sec2/Amp | T2 S-4 |
| Magnetic reluctance R | R | Amp2 sec2/Kg/m2 | S3 T-3 |
| Electric flux density | Jm2 | Kg m4/sec2 | ST |
| Electric field strength E | N/C or V/m | m Kg/sec3/Amp | T S-3 |
| Magnetic field strength H | Oersted or Amp-turn/m | Amp/m | T-1 |
| Poynting vector S | Joule/s/m2 | Kg/sec3 | S-3 |
| Frequency f | Hertz | sec-1 | T-1 |
| Wavelength l | metres | m | S |
| Voltage EMF V | Volts | m2 Kg/sec3/Amp | T S-2 |
| Magnetic/Vector potential MMF | MMF | Kg/sec/Amp | T2 S-3 |
| Permittivity e | Farad per metre | sec4 Amp2 /Kg/m3 | S2 T-1 |
| Permeability m | Henry per metre | Kg m/sec2/Amp2 | T3 S-4 |
| Resistivity r | Ohm metres | m3Kg/sec3/Amp2 | T2 S-2 |
| Temperature T | ° Kelvin | K | T S-1 |
| Enthalpy H | Joules | Kgm2/s2 | T S-1 |
| Conductivity s | Siemens per metre | Sec3Amp2 /Kg/m3 | S2 T-2 |
| Thermal Conductivity | W/m/° K | Kg m /sec3/K | S-1T-1 |
| Energy density | J/m3 | Kg/m/sec2 | T S-4 |
| Ion mobility m | Metre2/ Volts seconds | Amp sec2/Kg | S4 T-2 |
| Radioactive dose Sv | Sievert or J/Kg | m2/s2 | S2 T -2 |
| Dynamic Viscosity | Pa sec or Poise | Kg/m/s | T2 S-4 |
| Fluidity | 1/Pascal second | m sec/Kg | S4 T-2 |
| Effective radiated power ERP | Watts/m2 | Kg/m/sec3 | S-3 |
| Luminance | Nit | Candela/m2 | S-3 |
| Radiant Flux | Watts | Kg.m/sec3 | S-1 |
| Luminous Intensity | Candela | Candela | S-1 |
| Gravitational Constant G | Nm2/Kg2 | m3/Kg/s2 | S6 T-5 |
| Planck Constant h | Joules second | Kg m2/sec | T2 S-1 |
| Coefficient of viscosity h | n | Kg/m/s | T2 S-4 |
| Young’s Modulus of elasticity E | N/m2 | Kg/m/s2 | T S-4 |
| Electron Volt eV | 1eV | Kg m2/sec2 | T S-1 |
| Hubble constant Ho | H | Km/sec/Parsec | T-1 |
| Stefan’s Constant s | W/m2/K4 | Kg/s3/m/K4 | S T-4 |
| Strain e | - | - | S0 T0 |
| Refractive index h | - | - | S0 T0 |
| Angular position rad | Radians | m/m | S0 T0 |
| Boltzmann constant k | Erg or Joule/Kelvin | Kg.m2/s2/K | S0 T0 |
| Molar gas constant R | J/mol/Kelvin | Kg.m2/s2/K | S0 T0 |
| Mole n | Mol | Kg/Kg | S0 T0 |
| Fine Structure constant a | - | - | S0 T0 |
| Entropy S | Joule/Kelvin | Kg.m2/s2/K | S0 T0 |
| Reynolds Number Re | - | - | S0 T0 |
| Newton Power Number Np | - | - | S0 T0 |
Table 1. Borg’s Derived Physical Units
There are some of these we would take issue with, but, in general, it’s a great, independent, demonstration of progress in the use of the new concepts of space and time.
References (6)
-
 Response: event management company in chandigarh
Response: event management company in chandigarh -
 Response: chandigarh to dehradun taxi
Response: chandigarh to dehradun taxi -
 Response: sarkari job for 12th pass
Response: sarkari job for 12th pass -
 Response: best film schools in india
Response: best film schools in india -
 Response: tere ashkon se mujhpar
Response: tere ashkon se mujhpar -
 Response: tndte
Response: tndte
Reader Comments