The Larson Research Center

The discrete and continuous nature of space|time ratios in our RST-based theory of SUDRs and TUDRs is a new feature, but the vibration and wave analogs of these is not. We have seen that the expansion/contraction of a sphere, or spring, is a binary function, easily confused with the dual functions of sine/cosine, when the latter are represented as two, independent, springs, whose oscillations are given the proper phase relation, as commonly demonstrated in textbooks.

Nevertheless, when the expansion from point (local) to sphere (non-local) is analyzed, it is quite clear that it is an analog of binary rotation, or, maybe more correctly, binary rotation is an analog of the expansion/contraction function. In our case, this was discovered accidentally, when we happened to use GA to try to graphically illustrate the SUDR, TUDR, expansion/contraction here. Even more remarkably, however, it now turns out that when Hamilton discovered the quaternions, he immediately realized that the quaternion rotation was binary, but he ignored this fact, and, according to Simon L. Altmann, it wasn’t until 1958 that the mathematics community began to recognize it:

The first explicit statement to the effect that something is wrong here which I have been able to find is as recent as 1958 by Marcel Riesz…: ‘Hamilton and his school professed that the quaternions make the study of vectors in three-space unnecessary since every vector can be considered as the vectorial part.. .of a quaternion. ..this interpretation is grossly incorrect since the vectorial part of a quaternion behaves with respect to coordinate transformations like a bivector or “axial” vector and not like an ordinary or “polar” vector.’ However damning this statement is, it is only half the story, since the pure quaternion is not anything like a vector at all: we shall see that it is a binary rotation, that is a rotation by π.

Altmann believes that Hamilton’s motivation for disregarding the binary nature of the rotation of a pure quaternion is found in his need to “understand the physical, or geometrical, meaning of equating the square of the imaginary, or quaternion, unit, i², with -1.” Hamilton understood from Argand that “i² should be a rotation by π, which, duly enough, multiplies each vector of the plane by the factor -1,” writes Altmann, who then goes on to explain the crux of the matter:

For this reason, Hamilton always identified the quaternion units with quadrantal rotations, as he called the rotations by π/2. Clifford associates himself with this interpretation which he presents with beautiful clarity. The sad truth is that, however appealing this argument is, to identify the quaternion units with rotations by π/2 is not only not right, but it is entirely unacceptable in the study of the rotation group: we shall see, in fact, that they are nothing else except binary rotations.

Altmann is a recognized expert on the rotation group. He shows conclusively in this 1989 paper that Hamilton deliberately forced quaternions to fit his preconceived convictions of I² = -1, as a 180 degree rotation, even though he knew that the so-called “pure quaternion” (where the real part is 0) is a binary, or double, rotation, which presumably would make i² = -1 equate to a 360 degree rotation. Altmann quotes Hamilton’s admission of this in his 1853 Lectures on Quaternions:

…the SYMBOL OF OPERATION q( )q-l. where q may be called (as before) the operator quaternion, while the symbol (suppose r) of the operand quaternion is conceived to occupy the place marked by the parentheses.. .[can be regarded as] a conical transformation of the operand round the axis of the operator, through double the angle thereof, …

The parentheses are Altmann’s. It appears, though, that, in the special case of “pure quaternions,” either rotation, single or double, may be understood, and Hamilton’s choosing the single angle is interpreted by Altmann to be due to his focus on algebra and his notion of vectors, a notion that was not the same concept as what eventually came to be meant by his word vector:

…the status of vectors in this scheme is highly dubious, …in Hamilton’s approach rotations become subservient to the algebra, which opens the door to a variety of misinterpretations.

Altmann’s thesis, as indicated by his paper’s title, Hamilton, Rodrigues, and the Quaternion Scandal, is that Rodriques understood the binary nature of quaternion rotations, before they were discovered by Hamilton, but this was recognized only belatedly, and its significance is therefore unappreciated. He writes:

We must now discuss again the significance of the quaternion units. Because they are pure quaternions they must now be identified with binary rotations (rotations by π). This, for Hamilton, must have been absurd: the relation i² = -1 must still be satisfied. But the product of two rotations by r about the same axis is a rotation by 2π. This is clearly the identity operation, i.e., one which does not change any vector, whereas we are now saying that it is equal to - 1, i.e., that it changes the sign of all vectors in space. I believe that this is the reason Hamilton was forced to accept his parametrization, since this agreed with his picture of quaternion units as quadrantal rotations. Rodrigues, practical man as bankers must be, knew better than to worry about this strange result of his geometry-he did not carry, like Hamilton, all the world’s problems on his shoulders. Nature and history, alas, were playing games with Hamilton. How was he to know that Cartan was going to discover in 1913 objects (spinors) which are indeed multiplied by - 1 under a rotation by 2π, exactly as Rodrigues’s parametrization requires?

Moreover, when the topology of the rotation group became understood in the 1920s through the work of Hermann Weyl, it became natural to accept that the square of a binary rotation multiplies the identity by - 1 and thus behaves like the quaternion units. Though this should have shown the enormous importance of quaternions in the rotation group, they were by that time somewhat discredited, so that other much less effective parametrizations of the rotation group were in universal use. It must be stressed that the Rodrigues approach to rotations, by emphasizing their multiplication rules and by regarding them entirely as operators, fully reveals the group properties of the set of all orthogonal rotations, the full orthogonal group S0(3), as it is now called. The set of all normalized quaternions (in the Rodrigues parametrization) is a group homomorphic to SO(3) and it is its covering group.

Although I cannot go into the mathematical significance of this statement, its practical importance in quantum mechanics, e.g., can be easily understood: it permits the study of the transformation properties of the wave functions of the electron spin. It is for this purpose that quaternions are superb, because their use in dealing with rotations makes the work not only simpler but also more precise than with any other method.

But for us, of course, the significance of this confusion goes even further, because we have identified the scalar expansion/contraction of the SUDRs and TUDRs with a binary transformation, equating to 2π rotation. Hence, the mathematical expansion of a point to a sphere, and the contraction from a sphere to a point, can be represented as a full cycle, or 2π rotation, as shown in the figure below:

      

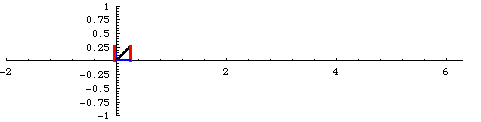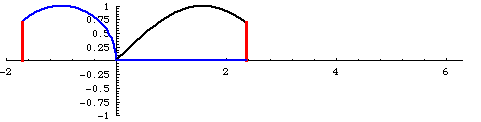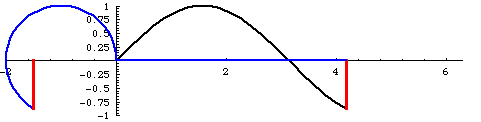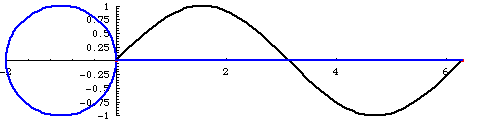
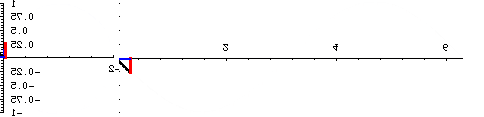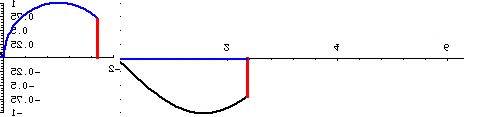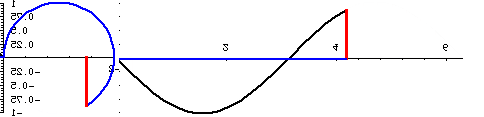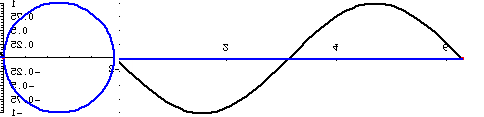
Figure 1. Sine Curves of Two, Reciprocal, Rotations

In the figure above, the phase of the curves is shifted 90 degrees relative to the rotations, from what they would normally be. The 0 points are at the top and bottom and the 1/1 point is at the center, so, when the rotations start, at the 0 point, the curves should start at the top and bottom, respectively. Also, the timing is off a little, but this will have to do until I can find the time to fix it. 

When a SUDR and TUDR are joined together in an S|T combo, the two, reciprocal, oscillations, represented as two, counter, rotations, must be represented as two, inverse, pure wave forms, but these are not the so-called positive and negative frequencies of the real sinusoid waveform that is so fundamental to physics, the canonical example of which is the mass-spring oscillator.

The new interpretation of the mass-spring oscillator, which we are employing, where the vectorial displacement of the mass, due to the restoring force of the spring relative to the equilibrium position, is not the important consideration, but rather the scalar expansion/contraction of the springs, in the two-spring configuration, is our focus. When we do this, we find that the two components of the real sinusoid take on a new meaning. Of course, as might be guessed, the new meaning has to do with a change from Hamilton’s quadrantal unit to Rodrigues’s binary unit, in the quaternions.

If the true quaternion unit is a binary unit, not a quadrantal unit, as Altmann points out, and this discovery is so germane to the study of groups and quantum mechanics, this appears to us to be an extremely important connection in our study of these scalar motions.

It shows that the representations of the 90 degree phase relation of the positive and negative components of the sinusoid,  the crucial element of Fourier transforms, are only part of the story.  It is important to recognize that the 180 degree, inverse, relation of two scalar magnitudes, the compressed and expanded states of the springs, or the S|T unit oscillations, that is associated with simple harmonic motion, can no longer be ignored. The S|T unit is analgous to a combination of sines and cosines, but now there are two, reciprocal, sinusoids, which we must consider that are composed of these.

Clearly, however, combining these two, 2π, units, does not result in constructive and destructive interference, as in the case of the quadrantal units, but rather in two, reciprocal, aspects of one function, as seen, for example, in the envelope of a modulated carrier wave, with a modulation index of 1, as illustrated below.

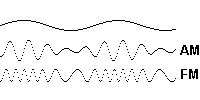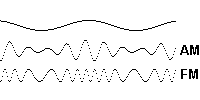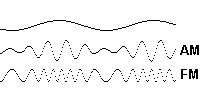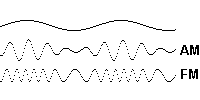
Figure 2. AM and FM Modulation of a Carrier Wave.

Interestingly, in the case of frequency modulation of a pure tone, we can clearly see that the information carried by the high frequency is the reciprocal of the information carried by the low frequency, which is a perfect analog, if not proof, of our compressed/expanded spring concept in representing these scalar oscillations as binary (2π) rotations. Of course, what’s not shown in the above graphic, is that there are always two side bands in a modulated carrier wave, one of which is regarded as redundant, and normally discarded.

Nevertheless, in treating each sinusoid, we use the usual equation of the function

x(t) = A (sin ωt + φ),

and then of course if the phase, φ, is shifted 90 degress, we get the cosine function

x(t) = A (sin ωt + π/2) = cos(ωt) 

both of which comprise the sinusoid signal.

But what equation do we use in treating both sinusoids of a modulated carrier? We need an equation for a single function of two binary rotations, and recalling that the double binary rotation (meshed gears) is the relation of two, reciprocal, aspects of two individual S|T units, joined in an S|T triplet, we can recognize something else, something that is profound: Equating the rotation of each gear to a sinusodial, one the reciprocal of the other, means that, since each of the two sinusodials is composed of a sine and a cosine, or phase quadrature, function, the analogy between our RST-based theory, with its discrete units of motion (SUDRs, TUDRs, and S|T combos), and the science of complex-number-based digital signal processing, with its discrete Fourier theory, is suprisingly and breathtakingly close.

It seems clear that, to the extent that we can take advantage of the well established principles in the science of digital signal processing, we can proceed to uncover the true relations of vector and scalar magnitudes, the continuous and the discrete, as they are reflected in the fundamental tetraktys of numbers and its associated algebras.

While this thought is as daunting as it is provoking, what choice do we have but to continue to follow our noses? Stay tuned.  

Update: I edited the text and added a graphic to clarify this post Oct 31, 2007