Square Roots & 1st & 2nd Orderings of the Periodic Table
In 1929, Charles Janet published his paper, “Deliberations on the Structure of the Nuclear Atom,” in which he proposed an interesting alternative to today’s Periodic Table of Elements. Although it has been almost completely ignored, his table was loosely based on the same 2n2 periodic relationship used in quantum mechanics, but, as shown in figure 1 below, with an interesting twist. The first period contains four elements!
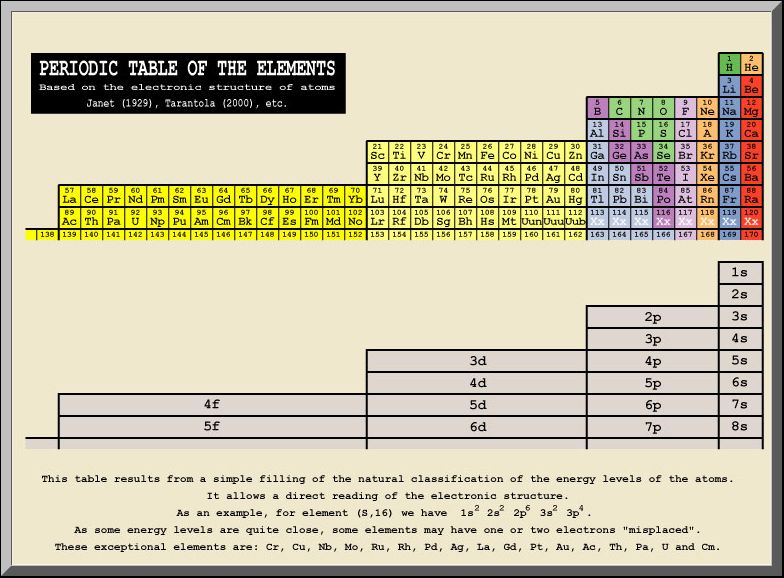
Figure 1. The Periodic Table of Charles Janet Published in 1929.
This table, appearing on Albert Tarantola’s website, is based on Janet’s work, which Tarantola refers to as the “first ordering” of the elements. It follows the accepted electron configuration sequence in ascending atomic order, so even though the two columns of akali metals and akaline earth metals are moved over to the right under hydrogen and helium, the accepted order of electron shell filling is maintained, as shown in table 1 below.
|
|
|
|
1s |
|
|
|
|
2s |
|
|
|
2p |
3s |
|
|
|
3p |
4s |
|
|
3d |
4p |
5s |
|
|
4d |
5p |
6s |
|
4f |
5d |
6p |
7s |
|
5f |
6d |
7p |
8s |
Table 1. Z-Ordered Electron Configuration of Janet Table (Read left to right, top to bottom)
This is interesting in the context of the LRC’s RST-based research, because the periods of Larson’s periodic table (here) are based on his 4n2 relationship, which requires four elements in the first period. Of course, it’s always been assumed that the three missing elements in the first period were incomplete elements such as the proton, neutron and electron (or neutrino, or massless neutron, etc.)
However, the placing of helium, lithium and beryllium into the first period is very interesting, although it “dethrones the noble gases from their key positions in the table, which is especially disappointing in view of the LRC’s Wheel of Motion form of the table.
Interestingly, as Tarantola and others have pointed out, another form of the table can be constructed from a ratio of square roots of atomic ionization potentials, as first shown by Le Cornec in 2002, using actual ionization data from the existing literature. Although Tarantola dismisses the significance of Le Cornec’s work, because he offers no theory to explain it, he does acknowledge that it shows a reversal in the order of the “s” and “p” energy levels, which, unlike Le Cornec, who asserts that this indicates a major failure of quantum mechanics, he simply attributes to the fact that the atom is a “complex object.” Tarantola calls this table the “second ordering” and leaves it at that.
For us, though, the fact that the ionization pattern shows a different order, inconsistent with the standard atomic model, is extremely interesting. One of the reasons why appears in the mapping of the s, p, d and f energy levels to the tetraktys. If we place these sets of 2 energy levels into the tetraktys, with subscripts indicating each, we get table 2 below.
|
|
|
|
2s |
|
|
|
|
|
|
2s |
|
2p |
|
|
|
|
2s |
|
2p |
|
2d |
|
|
2s |
|
2p |
|
2d |
|
2f |
Table 2. Duality of Electron Configurations Mapped to the Duality of the Tetraktys
As will be readily noticed, the energy levels map perfectly to the tetraktys, in some respects. There is one of the four dual “s” sets at the top, with the remaining three “s” sets positioned in the same repeating fashion, at the beginning of each row, as the 20 values in the tetraktys. The total number of sets is consistent as well, with four dual “s” sets, three dual “p” sets, two dual “d” sets and 1 dual “f” set, each set having two, six, ten and fourteen members, respectively (the difference between the successive 2n2 periods), arranged into four groups, corresponding to the four 4n2 periods of Larson’s table and the Wheel of Motion.
In fact, the only missing characteristic seems to be the accepted electron configuration order. However, Le Conec’s ionization’s order doesn’t comply either. As shown in figure 2 below, Tarantola’s table of second ordering takes lithium and beryllium out of the first period and puts them back into the second period, as indicated by Le Cornec’s ionization results.
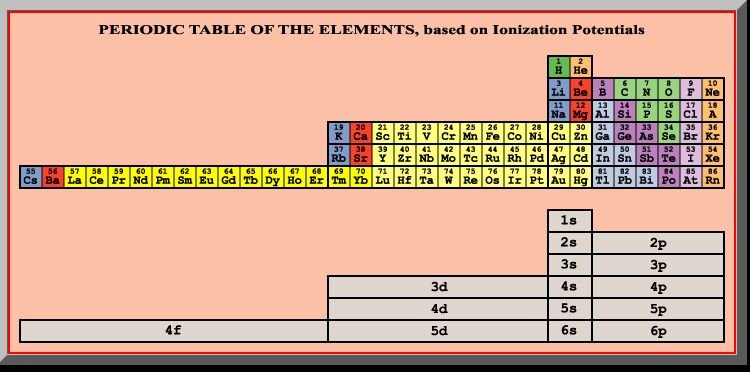
Figure 2. Tarantola’s Modification of the Periodic Table (Second Ordering) Given Le Cornec’s Results
But, if we take the fact that Janet’s table, based on a 2n2 period, concurs with Larson’s table, based on a 4n2 period, and the fact that Le Cornec’s results contradict quantum theory, based on a ratio of square roots, we have to take notice, because, as it turns out, the oscillating pseudoscalars (SUDRs & TUDRs) of the S|T units, contain both the 2n2 and the 4n2 terms, as the two factors in a series of ratios of square root products that fit the four periods of the table!
Again, the only thing missing is the order of the energy levels. If we map the four periods of the square root equations to the tetraktys, we get a perfect match, as shown in table 3 below.
|
|
|
|
2x4 |
|
|
|
|
|
|
2x4 |
|
8x16 |
|
|
|
|
2x4 |
|
8x16 |
|
18x36 |
|
|
2x4 |
|
8x16 |
|
18x36 |
|
32x64 |
Table 3. Duality of S|T 2n2 x 4n2 Periodicity Mapped to Tetraktys
Though, at first, this seems counter intuitive, it works because the equations of the table are based on the equation of inverse geometry (r’2 = r * r’’), where the inverse of a given circle’s, or sphere’s, radius, works out to be twice, or half, its radius. Students of the RST will recognize the significance of this immediately, since 1/2 and 2/1 are the basic units of speed-displacement in the system.
Details to follow soon.
References (1)
-
 Response: celebrity networth
Response: celebrity networth
Reader Comments (1)
THIS is the periodic table that our children should be learning in school, not that dingus Schrodinger's table!!!!