The Larson Research Center

The last time I posted an entry here was exactly a year ago yesterday. It seems impossible, but that’s what the date on the previous post indicates.

To say the least, I needed something interesting to write about, before the year ends. I did post an article about the LST preon theory published in the 2012 November issue of Scientific American, but I wanted something new to write about our RST-based theory of preons (RSt). To go on record in this momentous year 2012, with something significant, something to advance the theory, just seems important.

Well, in the general discussion the other day, the fact that the LRC’s RSt, unlike Larson’s RSt and unlike Peret’s RSt, is developed using mathematics, albeit a new mathematics, as well as logic, came up and I decided that I had better go back and reread it to refresh my memory, in order to be ready to answer questions about it.

Wow, was I surprised! Here, before leaving the LRC for six months, Larry the mathematician and I had been working out the mathematics of the SUDR and its inverse the TUDR in pursuit of the properties of the preons and thus the standard model particles. I had discovered my silly mistake of using the square root of two and its inverse in this endeavor, instead of the square root of three.

Big difference. Instead of dealing with neat values with a factor of 8, we were facing a somewhat awkward factor of 27! It takes 27 volumes of a SUDR to equal the value of one TUDR! I didn’t want to believe it. I tried and tried to figure a way out of it, but finally had to resign myself to the fact that we would have to work with it.

Then, to my utter surprise, I found it confirmed in the development of the new mathematics that I had written up four or five years ago. My doubts originated from the assumption of inverse geometry, where we used the equation r’2 =r x r”, to quantize the SUDR and TUDR and found that the SUDR volume is 1/27 the volume of the TUDR. Yet, writing years before learning anything about this equation, I had come up with the exact same thing, only in terms of poles!

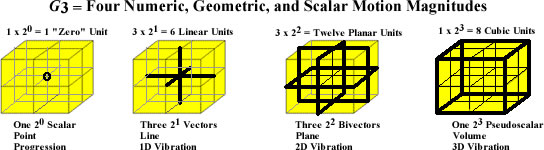
I had forgotten all about it, but counting the poles of the dimensions of the tetraktys,

1) 20 = 1

2) 20 + 21 = 3

3) 20 + 21 + 22 = 9

4) 20 + 21 +  22 + 23 = 27 

the 3D line, the fourth dimension counting from 0, contains 27 poles: 1 monopole, 3 dipoles, 4 quadrupoles and 1 octopole (1 + (3x2) + (3x4) + 1(8) = 27.)

Now, how do calculations of geometric ratios, using the equations for circumference, area, and volume, all requiring the use of pi, and employing the equation of inversive geometry, in other words, the use of equations of continuous magnitudes, turn out to be identical to calculations based on fundamental numbers, dimensions and polarities (“directions”), all based on discrete quantities?

A surprise it may be, but it is the truth. Check it out for yourself, dear reader.

It turns out that the connection is the sacred number three, the union of duality, which, impressively enough, is the very definition of the Reciprocal System, the fundamental of which are embodied in Larson’s Cube.

The graphic above is outdated, but appropriate, because when I developed the new mathematics, I had yet to even think about the inner and outer circles contained by the LC and also containing it. This is all I had at the time.

I think this is a worthy announcement, a discovery to match the year 2012, and just in the nick of time too!

:)