The Larson Research Center

Mathematics has a life of it’s own and has grown into an incredible array of complexity, layered like sediment in an ancient lake bed, over century upon century, by mathematicians. However, as Hestenes points out, the development of mathematics useful for physics is not the responsibility of mathematicians, but physicists, and history has shown that this line of mathematical development has generally resulted from successful attacks on physical challenges.

Today’s crisis in theoretical physics, precipitated by contradictions at the fundamental level, with respect to the discrete vs. continuum characteristics of nature, is generating new mathematics, but it is producing mathematics that is extremely complex, elaborate and baroque and not necessarily useful for physics, yet (string theory). Maybe this is because today’s physics has become so mathematical, that the mathematical physicists are more interested in researching the principles of mathematics than they are in researching the principles of theoretical physics.

Here at the LRC, we work with a brand new principle of physics, called scalar motion, and a “new” principle of mathematics, the operational interpretation of number, in an effort to form a brand new science, based on these principles, called scalar science. To many investigators of Larson’s Reciprocal System theory (RSt), which he developed from his Reciprocal System of Physical Theory (RST), the lack of an appropriate mathematical formalism is painfully evident. Yet, at the LRC, we have discovered that Larson provided the fundamental insight for what we now are calling scalar mathematics and that it is much more than a modern mathematical formalism; It is the discovery of a fundamental principle of mathematics that is founded on the same underlying reality as is the fundamental principle of motion - the principle of reciprocity.

In the modern LST community, the major principle of mathematics guiding the research of theoretical physics is symmetry, and the mathematical formalism upon which it is based is called group, and group representation, theory. Specifically, it is a special type of group, called a Lie (Lee) group that is most useful to the physicists. In fact, it’s a special type of Lie group, called a simple Lie group that the LST community is mostly interested in, and within these, it is the complex ones that they use most, and especially the ones in compact real form.

Hence, when authors refer to Lie groups, and their associated Lie algebras, the term has to be qualified, because of the complexity of the subject. For instance, one could be concentrating on “compact real forms of complex simple Lie groups” and refer to these groups as Lie groups for brevity, but obviously the term is highly qualified. Needless to say, however, the complexity involved in the use of these concepts is tremendous and very daunting for neophytes, wanting to learn how to study physics, based on the simple principles of symmetry.

Fortunately, the principle of reciprocity is the epitome of symmetry. Hence, at the LRC, mastery of Lie groups and Lie algebras is not a prerequisite to study the role of symmetry in physics. The only prerequisite here is a thorough understanding of the principle of reciprocity. Consequently, we begin at the beginning in mathematics and physics, with the fundamental definitions of units, dimensions, and directions in defining the magnitudes of motion, and the spaces of geometry, with numbers.

Nevertheless, we can, and many times do, refer to LST concepts to connect the new with the old, because it’s important to understand that scalar science does not replace vector science, but is actually an extension of it. In our effort to demonstrate this, and to clarify the relation between scalar science and vector science, we focus on the ancient Greek concept of the tetraktys, or the first four numbers, 1, 2, 3, and 4, which, to the ancients (not only the Greeks), contained the mystery of the cosmos.

It is in the tetraktys that we clearly understand the connection of geometrical units and numbers, and have discussed the work of Hestenes a great deal, in this connection, because he was the first to emphasize the importance of Clifford algebras as geometric algebras (GA), and how they can be used to great advantage in the study of physics. In fact, it turns out that 3D Clifford algebra is the Lie algebra of physical space, and since Lie algebra is the infinitesimal group of the Lie group, or elements of the Lie algebra are elements of the groups that are “infinitesimally close” to the identity of the group, every field and geometry in physics can be described by Clifford valued forms (see: Garrett’s tutorial on Physics Forums).

However, it’s important to understand that the study of symmetry in this way necessarily includes the concept of rotation in connection with the dimensions of geometry, and the concept of the smooth manifolds of topology, which increases the complexity of the subject immensely. This is especially so, given that the concept of rotation is obtained through the ad hoc invention of the imaginary number. While GA replaces the concept of rotation in terms of complex and hypercomplex numbers, with a much more compact, intuitive, concept of rotation, which helps somewhat, it doesn’t simplify the complexity of using differential forms and vectors to describe the symmetries of interest, the symmetries of the standard model of particle physics, SU(3)x(SU(2)x(U(1).

Fortunately, however, the knowledge of scalar mathematics is shedding a good deal of light on the subject and clarifying the concepts involved. We’ve seen how the operational interpretation of rational numbers (OI) makes it possible to define two “directions” of numbers (positive and negative) without recourse to the ad hoc invention of the imaginary number, i, where -1 is defined as its square. With the OI, we define negative numbers with the principle of reciprocity instead. If we consider the three dimensions of the universe of motion in light of the OI, instead of i, we see a remarkable clarification of what n-dimensional numbers actually are. Indeed, we can again see why the tetraktys is so central.

Figure 1, below, shows the four numbers of the tetraktys in terms of dimensions of motion and dimensions of spaces. We recall the words of Newton, who pointed out that principles upon which the spaces of geometry are defined, are not principles of geometry, but come from “without,” from another dimension, if you will. In figure 1, we see that these principles are actually the three dimensions of the tetraktys, 0, 1, 2, and 3.

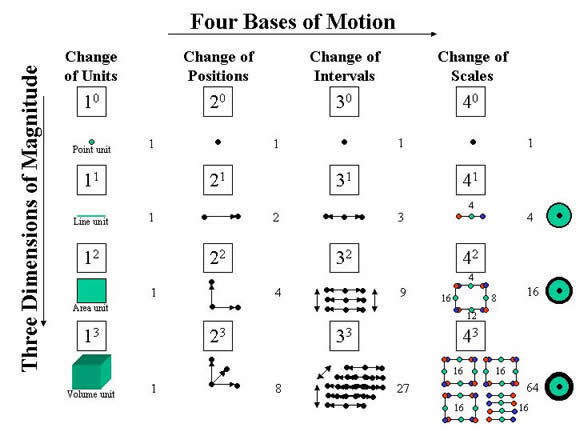
Figure 1. The Four Dimensions of Motion

In the first column of the chart in figure 1, we see the first dimension of motion, or what we will call the first base of four bases of motion, to distinguish them from the four dimensions of magnitude.  This is the number 1 of the tetraktys, as it increases in geometric dimension, row by row, corresponding to the unit point, unit length, unit area, and unit volume spaces, or distance measures, of Euclidean geometry. Of course, 1 is 1/1 in the OI, and, as a scalar number, can be raised to any power, (1/1)ⁿ = 1, but its geometric dimensions are: 1, 1x1, and 1x1x1, the unit line, the unit plane, and the unit volume, the “right lines and circles” of geometry, to use Newton’s phrase.

However, these units of space, can only be created by motion, and the first dimension of magnitude of the first base of motion is zero, or no motion. Hence, these units are the potential spaces of geometry, which must be created by magnitudes of motion, a reciprocal relation of space and time.

The second column of the chart shows the second base of motion, or the number 2 of the tetraktys, as it increases in magnitude dimension, row by row, corresponding to the change of position between two points. Again, 2, to the zero power of magnitude, is no motion, which is equivalent to the number one, or a geometric point, but the three non-zero magnitude dimensions are: 2, 2x2, and 2x2x2, representing the separation of two points in magnitude dimension 1, the separation of four points in magnitude dimension 2, and the separation of eight points in magnitude dimension 3, corresponding to the magnitude dimensions of this motion required to define the unit magnitude spaces of column one; that is, with the base 2 motion, we can define a line in one dimension of magnitude, by separating two points; We can define an area in two dimensions of magnitude, with this motion, by separating two points in two orthogonal directions (2²), and we can define a volume in three dimensions of magnitude, with this motion, by separating two points in three orthogonal directions (2³).

However, notice that all the units of space defined by base 2 motion are necessarily positive units. This means that the numbers constructing the spaces with this motion are all positive. If it is unit distance we are considering, then we can produce the unit line, the unit area and the unit volume, as real objects, but since space is not an independent entity, both space and time are required to construct the spaces. In this case, the motion that separates the points must be in one direction at a time, so that to define an area requires two instances of the motion, and to describe a volume requires three instances of the motion. Moreover, a rotation of ninety degrees must separate each instance of the motion; that is, without the concept of rotation, we cannot transform the motion from one dimension to the next. Does this mean we need the imaginary number?

The answer is obviously no, in this case, because all the spaces to be defined are positive. All that we need is two rotations to orthogonal angles, which are defined by the unit spaces of column one. If we define the distance in one direction, with the number x/1, and the distance in an orthogonal direction with the number y/1, and the distance in a direction orthogonal to both the preceding directions with the number z/1, we can define the three required spaces. We conclude, then, that geometric orthogonality is achieved in base 2 motion through rotation.

The next base of motion is the third base, base 3 motion, corresponding to the number 3 of the tetraktys. Again, the zero geometric dimension of this motion is no motion, which is equivalent to the point. However, the first dimension of magnitude, of the base 3 motion, requires a separation of three points; the second, requires a separation of nine points, and the third dimension of magnitude requires a separation of twenty-seven points, or 3, 3x3, and 3x3x3.

Since base 3 motion defines a line with three points, the distance separating the points is constructed by two, simultaneous motions in opposite directions with respect to the center point. Since the inverse of x/1, y/1, and z/1, is 1/x, 1/y, and 1/z, we can see that when x, y, and z = 1, then there is no way to distinguish any of these numbers from any other. In other words, they are all equal to 1/1, when x, y, and z = 1, so this value forms the intersection of all non-unit values of x, y, and z. In the case of one geometric dimension, increasing the values of x, from 1 to 1+ n, increases the distance from 1/1 in both directions simultaneously. The same for values of y and z.

Consequently, if the first instance of base 3 motion creates a line between the two opposing values of x, by virtue of a linear expansion between three points, then a subsequent expansion in the y or z direction will expand the initial linear expansion in the orthogonal direction in two opposing directions. This creates an area consisting of nine points (an area of three, three-point, lines). A final expansion in the remaining orthogonal direction, produces the required volume consisting of twenty-seven points (a volume of three, three-line, planes).

Notice, however, that in the case of base 3 motion, the concept of rotation through an angle is not implicit. The rotation of a line along its longitudinal axis is not defined in this motion base. So, we conclude that the transformation from one dimension of magnitude to the next does not require rotation in base 3 motion. We will come back to consider the implications of this fact below, but for now let’s just be sure to note that the spaces of this motion, produced by a change of interval, or we might say by an expansion of an interval, involves two, opposed directions, a negative and a positive direction, with respect to the center. However, just as stretching a rubber band in two, opposite, directions does not make half of it positive and half of it negative, so too in this case. The n-dimensional spaces defined by base 3 motion are all positive. This is an important observation, the discussion of which we will also defer until later.

Finally, the fourth column of motion, base 4 motion, is the row by row geometric expansion of the last number of the tetraktys, the number four. As indicated in figure 1, whereas, base 2 motion is defined by change of position, and base 3 motion is defined by change of interval, base 4 motion is defined by change of scale. In the previous dimensions of motion, we indicate change of position in one direction by adding units of distance to the initial value of 1 unit, but with the OI, the value of 1/1 replaces zero, which is not a number. Hence the actual distance magnitude is a displacement from 1, not zero. For example,

x = 1/1 = 0,

because there is no difference between the denominator value, and the numerator value; that is, there is zero displacement between the two aspects of the number. The displacement, or the value of the relation of the numbers defines the magnitude, not the value of the numbers themselves (see: John Baez’s discussion of torsors). Thus,

x = 2/1 = 1; 2x = 3/1 = 2; nx = (n+1)/1 = (n-1), when n > 1.

Of course, the inverse of these magnitudes gives us the values of negative directions (remember, not negative spaces, but negative direction):

-x = 1/2 = -1; -2x = 1/3 = -2; -nx = 1/(n+1) = -(n-1), when n> 1.

In base 2 motion, there is motion in only one direction (positive). In base 3 motion, there is motion in both the positive and negative directions simultaneously, as shown in figure 1. Now, in both of these case, the motion defines the magnitude, by moving an object; that is, the units of x, y, and z are units of distance produced by the change of position of an object (separation of two points) over time, or the expansion of an interval (separation of three points), over time. However, in the case of base 4 motion, no object is involved in the motion, and the units of distance and time are always unit distance and time, so while it’s related to base 2 and 3 motion, base 4 motion is also very different.

Scalar motion is a measure of the progression of space and time, where space progresses just as uniformly and eternally as time does. Discrete units of this motion are created when the progression of one or the other of its two reciprocal aspects is continuously increasing and decreasing between two successive values, such as n and (n - 1). Thus, the alternating aspect increases at half the rate as the non-alternating aspect, producing a displacement in the rates of increase of the two progressing aspects. Consequently, the space/time ratio, or velocity, of the motion, in a displaced unit, never changes, but the scale of the displacement does change; that is, just as the ratio of 50/100, or 25/50, or 5/10 is all the same ratio, namely 1/2, the scale of 50/100 is very different than the scale of 1/2.

Since this is the case, what we are measuring in base 4 motion is units of velocity, and inverse velocity, not units of space. The unit of space that participates in the calculation of the velocity, is three-dimensional, because an increase/decrease in volume is the scalar magnitude in a 3D universe. It is the increase of the scalar point to the 3D pseudoscalar volume, as shown in column four of the chart in figure 1. Again, the first dimension of magnitude of the number, the zero dimension, is not detectable as motion, because no displacement can occur in a zero-dimensional system, and, like all the other numbers before it, 4⁰ motion is equivalent to the point.

However, with one dimension of magnitude, two displacements can be formed, as before, where either the value of the denominator or the value of the numerator, becomes greater than its reciprocal. Nevertheless, with no object to define the motion, the values of denominator or numerator cannot can be increased independently, like the numbers on an odometer. Only when the alternating increase/decrease pattern in the progression of one of the two aspects of the unit motion occurs, at a given point in the progression, can the 1/2 (one negative unit), or 2/1 (one positive unit), displacement occur. Therefore, the minimum number of progression units over which an alternating pattern can occur is two units. In other words, if the space aspect of

ds/dt = 2/2,

is alternating between increase and decrease, then its rate of increase will be reduced to every other unit, while the time unit continues to increase with every unit of progression. This conditions alters the increasing space/time ratio to

ds/dt = 1/2,

or, in the case of the alternating progression of the time aspect, to

dt/ds = 1/2,

representing a negative and positive unit of motion, when the dt/ds unit is inverted to ds/dt = 2/1. Combining these two units, then, is essentially combining two units of 2/2 progression, which is a total of 2/2 + 2/2 = 4/4 units of progression. However, one unit of space in the negative unit, and one unit of time in the positive unit, the decreasing units, can be combined separately to provide a numerically correct equation of the motion:

ds/dt = 1/2 + 1/1 + 2/1 = 4/4 num,

where num is short for natural units of motion. Notice the similarity of displacement in this motion and the displacement of the base 3 motion with 1 dimension of magnitude. The difference is that the displacement of the base 4 motion is not one unit of distance expansion in the negative direction, but one unit difference in the progression rate of space/time; that is, in the ds/dt = 1/2 value of base 4 motion, the progression rates of space and time are displaced so that the rate of time progression is twice the rate of space progression, over two units of progression. In effect, this displaced velocity is one half the unit velocity of the undisplaced progression, where the rates of the space and time progressions are equal.

Thus, while the two velocities (ds/dt = 1/2 and ds/dt = 2/1) are equal in terms of their displacement from 1/1, in their respective “directions,” they are unequal in terms of their velocities, as the velocity of 2/1 is four times as fast as the velocity of 1/2 (2/.5 = 4). Note, however, that the velocities are actually one cycle of increase/decrease values, or frequencies. The important thing to understand is that the “distance” between the two frequencies is one unit of magnitude in one “direction” and one unit of magnitude in the opposite “direction,” relative to the unit value in the center, which is isomorphic to a one-dimensional line of magnitude four.

Thus, in the next row, with 2 dimensional magnitude, the value of the “area” magnitude is 4x4, or four times the “line” magnitude, which can be illustrated by arranging four “lines” of magnitude as four lines in a square, even though, no rotation of the “line” is conceivable. Likewise, with 3 dimensional magnitude, the 4x4x4 magnitude of motion can be arranged to form a cube, even though this is just an equivalent to the total 1D magnitudes of motion contained in the unit 3D magnitude.

What this shows, then, besides the unity of dimensions of numbers and the magnitudes of geometry, is that the symmetry of motion can be dramatically demonstrated, without the use of imaginary numbers, or even the concept of rotation.  That is to say, we can see now that rotation has only a limited role to play in the total picture of motion.  It is only applicable to the base 2 motion of the tetraktys, while the real key to understanding symmetry, the principle of reciprocity, is orders of magnitude more powerful.

Later, we will discuss how these dimensions of motions form groups, and what that means in terms of group theory, but that’s all for now folks. 

Update:  8 Dec 06 - I’ve edited the text to correct errors in references to the various bases of motion.  I appologize for the confusion in the original text, which was caused by confusing dimensions of magnitude with dimensions of motion.  Changing the terminology helps to keep the concepts clearer and to avoid mixing up the numbers as I did.  I hope it’s easier to understand now.