The Larson Research Center

Note: This article was inadvertently published on March 3rd, before it was completed. The completed article was published two days later, on March 5th.  

In the previous post, we discussed the effect the Chart of Motions (CM) has on the concept of the so-called incommensurable, or irrational, numbers.  In short, when it’s realized that the concepts of numbers and magnitudes are naturally unified, we see that there is no need for the ad hoc inventions of real, imaginary, and compactified numbers.  However, this is a startling conclusion, given that the whole of modern science and technology is built on the use of these ad hoc concepts, and, as they say, extraordinary claims demand extraordinary proof.

Nevertheless, while it’s true, at the moment, that we don’t have the necessary proof, but are only conjecturing that this is the case, having a rational basis for making such a conjecture (no pun intended) is still impressive. The foundation of the claim rests on Larson’s discovery that the nature of space is not the distance, area, or volume defined by a set of points, satisfying the postulates of geometry, but rather the reciprocal of time, in the equation of motion.  This discovery changes everything, and it changes it profoundly.

We know that time marches on incessantly, independently, regardless of observation or agency.  Now Larson’s work shows us that, if the march of time is endless, then there must be a, reciprocal, march of space as well.  In other words, the observation of the universal, eternal, increase of time, tells us that there must be a universal, eternal, increase of space as well, by definition.  In short, there is a universal, eternal, motion in nature.  In fact, we can measure both the time aspect and the space aspect of this motion, by observing distant galaxies with powerful telescopes, as Hubble was the first to discover.

There are many consequences of recognizing this new, universal, motion, but one of the most important, and relevant to understanding numbers, is that what we call “distance” between points is not space that exists independently and that has any kind of properties.  The proof of this is that space cannot be measured independently of time, and time cannot be measured independently of space.  To measure the distance between points, either in terms of space, or in terms of time, requires motion, or both space and time, reciprocally related.  In other words, to measure, or calculate, the distance between physical points in a coordinate system, the motion that separated the points, or will separate the points, must be measured. 

The magnitude of the motion measured is not necessarily important, unless it is used as the basis for calculation.  For instance, if measuring the distance by eye (perspective) the speed of the light traveling over the distance is not important, or, if measuring by a standard rod or tape, the speed of the act of placing the device between physical points is not important, but motion of some magnitude must take place between the points, in order to measure (estimate) the distance. On the other hand, If time is used to measure the distance, as when timing the motion between the points, then the speed of the motion must be known in order to calculate the distance, as when lasers, radar, or sonar are used to measure distance.

Without exception, however, distance cannot be measured independently.  It is the space aspect of motion that must be determined, in order to measure the distance between points.  What this implies, as explained in the previous post below, is that there is not a one-to-one correspondence between numbers and the infinite points of a continuum, as assumed by most, and as regarded as “consummated” by the work of Cantor-Dedekind.

The fundamental postulate of the Cantor-Dedekind complete ordered field, which constitutes the so-called real numbers, is that the geometric linear continuum corresponds to the arithmetized real continuum,  where there is an irrational number between every pair of rational numbers, and a rational number between every pair of irrational numbers, leaving no gaps, if you will.  However, now we see that if there is no continuum of points in space, as assumed, but only motion that can be measured, then the need for a continuous set of numbers with no gaps makes no sense.  What needs to be “complete” is the set of ordered motion magnitudes, not a set of ordered space magnitudes.

Wikipedia describes the “Dedekind-cut” basis for real numbers as follows:

The Dedekind cut resolves the contradiction between the continuous nature of the number line continuum and the discrete nature of the numbers themselves. Wherever a cut occurs and it is not on a real rational number, an irrational number…is created by the mathematician. Through the use of this device, there is considered to be a real number, either rational or irrational, at every point on the number line continuum, with no discontinuity.

Of course, the reason the legacy system of mathematics (LSM) mathematicians feel the need to create irrational numbers is their assumption that a “number line continuum, with no discontinuity,” is required, because they assume that the physical magnitudes between points is space and that space is continuous, and therefore they reason that the discrete concept of number must be changed to correspond to the continuous concept of space magnitude.  However, the assumption of the RST is that the distance between points is the space aspect of motion and that the fundamental form of these magnitudes is both discrete and continuous, therefore it follows that, in a universe of nothing but motion, there is no need of ad hoc irrational numbers.

Another way to look at what is happening is to consider a Cauchy sequence as the basis for creating irrational numbers.  A Cauchy sequence is a sequence of rational numbers whose elements become closer as the sequence progresses.  In other words, the sequence should converge on the “real number line continuum,” meaning that a metric “space” in which all Cauchy sequences converge to the limit, a necessary concept of calculus, can be called complete. However, the only way to make a sequence of rational numbers converge completely (“to the limit,” as they say), thus corresponding to the continuity of a metric “space,” or measurable distance, is to include the invention of irrational numbers along with rational numbers in the set of real numbers.

By defining a Euclidean metric “space,” or distance, in terms of a function, called a “norm,” Pythagoras’ theorem can be used, as the defining function, in which the hypotenuse of a right triangle defines the “space” measure, or metric. Thus,

1) a² + b² = c² 

when a and b are real numbers, constitutes both the rational and irrational, or “real,” set of numbers.  In other words, any value of c can be expressed as a function of a and b, but only if a and b are allowed to be both rational and irrational, or real, numbers, and not if a and b are limited to rational numbers.

With the light of the new RSM, however, which incorporates the reciprocity concepts of the RST, the apparent incommensurability, inherent in the multi-dimensional numbers of the Pythagorean theorem, is completely misleading. What’s not commensurable is the idea of a continuum of motion and a continuum of space, not continuous space magnitudes and discrete numbers. If there is no independent space, then there is no continuum of space, and, therefore, there does not need to be a continuum of numbers that is in a one-to-one correspondence with the points on a line.  What needs to be logically complete is the discrete set of possible numbers that corresponds to the discrete set of possible physical magnitudes of motion, not the continuous set of possible numbers that corresponds to a continuous set of possible physical points of space.

Nevertheless, without the concepts of motion clarified by the CM, the fact that the change of position motion (M₂ motion) can take any one of an infinitely continuous range of values, not just a set of discrete values, argues to the contrary.  It is only when we recognize the differences between the three types of motion, M₂, M₃, and M₄, and how they relate to one another, that we can comprehend how discrete values of magnitudes of M₄ motion can make continuous values of M₂ motion possible.

It’s not difficult to understand this in a universe of nothing but motion, because, in such a universe, points in metric space don’t exist apriori.  To define metric space, one must define points first, and the only way to define points, in a universe of motion, is through discrete magnitudes of motion.  In the CM, we see that discrete points are defined by discrete magnitudes of M₄ motion.  Therefore, it follows that M₄ motion must precede M₂ motion.  Once two, or more, such discrete points exist, the separation of their locations is a measure of the past motion that separated them, which can be M₄ or M₂ motion.

Consequently, we may regard M₄ magnitudes, as more fundamental than M₂ magnitudes of motion, and it then follows that it is these discrete magnitudes of M₄ motion that discrete numbers should correspond to, not the continuous magnitudes of M₂ motion.  Fortunately, this appears to be the case.

We find that the insight of the universal progression, from which we assume the entire structure of the physical universe is derived, gives us a clear understanding that, contrary to LSM concepts, the natural numbers do indeed have the three properties of magnitude:

1. Quantity
2. Duality
3. Dimension

In order to understand this, the use of the RSM’s operational interpretation (OI) of number is required, wherein a “norm” of magnitude is defined by a function,

2) m|n = i

where m and n are natural numbers and i is the difference between m and n, called a displacement.  When m > n, i is positive. When m < n, i is negative.  When m = n, i is zero.  The operator, ‘|’, is used in a similar manner as the division operator, ‘/’, but does not signify a quotient, but only a reciprocal relation between m and n, the value of i.  Thus,

3) |m|n| = |n|m|

or the absolute value, the displacement of  -i, is equal to the absolute value, or displacement, of i.  Given OI numbers, the equation

4) m|n = 1|1 = 0 

is regarded as a statement of equivalence, such that m has the same, but inverse, value of n, as do equal weights on a pan balance, zero indicating the balance between equal magnitudes, similar to the financial concepts of debits and credits, where a series of transactions results in debts and assets that are calculated on a balance sheet, to determine the net worth of an individual, at a given point in time.

However, while OI numbers are not dynamic themselves, they can nevertheless represent relative rates of change, and, thus, changes in relative rates of change.  But this brings up an interesting aspect of OI numbers.  Whereas, in the traditional quantitative interpretation (QI) of number, used in the LSM, there is no difference in the numbers

5) 1/1 = 2/2 = 3/3 = n/n,

there is a difference in the OI case,

6) 1|1 < 2|2 < 3|3 < n|n,

just as there is a difference between the debts and assets of a millionaire and a pauper, even though the net worth of each can be the same, namely zero, whenever their respective debts and assets are equal. Consequently, this fact implies that the OI numbers are ordered, in increasing order, as shown in the sequence of equation 6), unlike the QI numbers in the sequence of equation 5). Furthermore, we can see that the numbers of equation 6) are ordered by size, because each successive number in the sequence contains one more possibility of distribution than its predecessor, just as n units of weight on a pan balance do.

In a pan balance, there is no freedom of choice for weighing 1|1, but there is one degree of freedom for weighing 2|2, two for 3|3, and so on; that is, in the case of 2|2, the number can be balanced, or unbalanced by one unit, in either direction; for 3|3, the number can be balanced, or unbalanced by two units, in either direction.  This can be expressed as an increasing number of numerical combinations, using OI numbers, as,

(1|1); (1|2, 2|2, 2/1); (1|3, 2|3, 3|3, 3|2, 3|1)… 

That the number of possibilities, as n|n goes to infinity is complete is obvious. There are no other possibilities, yet these infinite possibilities are contained in unit values formed by n|n = 1, and, therefore, they can be regarded as increasing divisions of unity, just as much as the two terms of equation 1) are regarded, in the LSM, as the function defining the Euclidean norm of a space metric.  However, while the LSM mathematicians must create irrational numbers, in order for the numbers a and b to converge on all values of c, nothing has to be created in the RSM.

To see this more clearly, consider the LSM and RSM numbers lines depicted below:

Figure 1. Two Number Lines

Again, the postulate of the real number system is that the geometric linear continuum corresponds to the arithmetized real continuum,  where there is an unidentifiable irrational number between every pair of rational numbers, and a rational number between every pair of unidentifiable irrational numbers, leaving no gaps.  In other words, the rational number line is incomplete.  To complete it, the idea of unidentifiable irrational numbers was defined, or invented, and, when added to the rational numbers, the irrational numbers complete the incomplete rational number line, which is then called the “real” number line.

However, as shown in figure 1 above, in the RSM, there exists another complete set of numbers that has nothing to do with the geometric linear continuum.  The OI numbers of the RSM form an infinite set of ordered numbers, each equal to 1.  In spite of this seeming contradiction, the elements of this ordered set actually constitute ordered subsets of denser and denser subdivisions of one, as can be clearly seen in the “meter” analogy of figure 2 below:

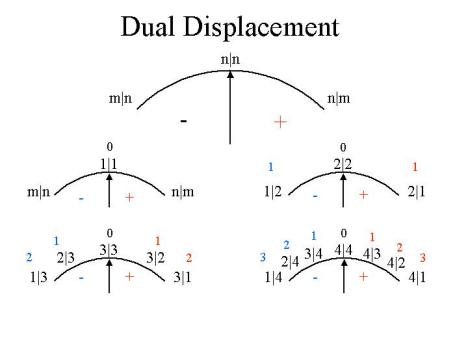
Figure 2. The Meter Analogy of OI Numbers 

In the “meter” at the top of figure 2, clearly there can be no displacement, because, 1 is not sub dividable, but 2 can be subdivided as shown, 3 even more so than 2, 4 more so than 3,  and so on, with each successive number in the set being more sub dividable than its predecessor.  Each number in the order is more sub dividable, thus larger, than the previous number.

That the ordered set is complete is easily seen in that there are no other possibilities between the successive numbers, unlike the infinite points on a geometric linear continuum, where there always must be a midpoint between any two points.  Thus, we see that the invention of the “real” number system is a misguided attempt to force the discrete number system into a one-to-one correspondence with the points of the geometric linear continuum, when actually they form a different sort of continuum, a continuum of operationally interpreted ratios, if you will.

The next step is to show that this set of OI numbers is not only ordered and complete, but also constitutes a field.  However, we’ll have to address that subject later.