The Larson Research Center

In the last entry, we discussed the mathematics of Larson’s cube (LC) and saw how one can calculate the ratios of the associated inverses, based on a 2D number system, using the square root of 2 and its inverse, analogous to the linear number system based on 1 and its inverse, but incorporating a change in the constant of proportionality.

Hopefully, this new ratio will prove useful, but we can extend it to the two balls that are defined by the LC. The diagonal of a 1x1x1 cube is the square root of 12 + 12 + 12 = 3, and since the radius of the outer ball of the unit LC is the diagonal of the unit cube, then we can use this radius and its inverse as the basis of the 3D number system, and the corresponding tetraktys.

To extend the inverse numbers, defined by the inverse LC to infinity, we simply calculate the reduction of the length of the sides of the current cube by the 45 degree rotation of its side to obtain the side length of the new cube, and then multiply this number by the square root of 3 to get the reduced radius and plug it into the appropriate formula for the diameter, surface area and volume of the ball.

This gives us a 3D number line, analogous to the 1D and 2D number lines we have already compared:

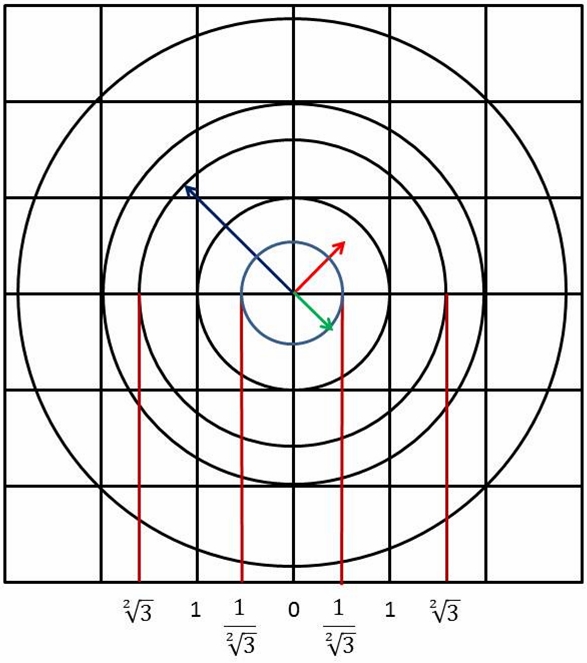
Figure 1. The the Right Lines and Circles of the 3D Number Line. 

It’s important to note that the projected radius of the 3D outer ball is larger than the radius of its 2D cross section counterpart, since its actual third dimension must be large enough to just contain the eight corners of the unit LC. However, if the larger radius (31/2) were actually rotated out of the page, into the third dimension, it’s clear that it would appear to shrink to the 2D size of the cross section (21/2). Therefore, the 2D projection, or representation, of the 3D outer radius is actually larger than the boundary of the unit cross section. 

The inverse is true for the inner ball: Its 2D representation must be smaller than the 2D boundary because its unit length is rotated out of the page and projected onto the cross section from above it. Hence, to show the true length on paper, the outer 3D radius is rotated onto the page, increasing the length of its projection onto the cross section, while the inner 3D radius is rotated out of the page, decreasing its projection onto the cross section.

It was this nuance that escaped my notice and introduced errors into the calculations that I was pursuing earlier. 

More later.