They Say Beauty is in the "i" of the Beholder
I posted a new excellent video in LRC Lectures Online by John Baez that explains the LST view of the mathematics that is so important to understand, as background to the development of an RST-based theory of particle physics here at the LRC.
In his video, John talks about the tetraktys, but he doesn’t call it that. He tells the math history of imaginary numbers and their use to devise higher-dimensional algebras from the reals. He explains the important concept of normed division algebras and how they only exist in certain dimensions, and how that fact kept Hamilton frustrated for a long time, as he sought to find a three-dimensional normed division algebra (although he didn’t have a label like that to express it concisely). “Normed,” in this context, means that the absolute value of the products is equal to the product of the absolute values.
The problem is, Baez and company have changed the meaning of the word dimension, without explicitly pointing it out to non-specialists. Their use of the word doesn’t necessarily refer to geometric dimensions, but, like Larson explained, the word dimension, for them, means the number of independent magnitudes in an equation.
Thus, complex numbers (ℂ) are two dimensional numbers for modern mathematicians, because they consist of a real and an imaginary part (a+ib), and they are used in calculations of 2D rotation.
However, in terms of the RSM, line 2 of the tetraktys (11), or 1(2^0), 1(2^1) in its binary expansion, defines a one-dimensional line:
(-) (+)
2^0 = 1 is the magnitude of the point in the middle, 1/1, and 2^1 = 2 is the one dimensional magnitude, with two opposite polarities, or a dipole, stretching out on either side of the point. In other words, it is the numerical equivalent of a geometric line in one dimension.
Hamilton finally realized that he needed four terms to construct what he thought of as a 3D algebra, moving one dimension up from what he thought of as a 2D algebra. He suddenly realized one day that he could accomplish his objective with one real number and three imaginary numbers, or what mathematicians would call a 4D number a+ib+jc+kd.
Today, these numbers are called quaternions (ℍ), and Baez refers briefly to the battle that ensued as to whether these allegedly “4D” quaternion numbers, or the allegedly “2D” complex numbers were the numbers of choice to use in science and engineering.
The champions of (ℍ) lost, and (ℍ) descended into the dusty bin of academics for a long time, but the important thing to understand is that they are actually 2D numbers, not 4D numbers! Think of them as a scalar, s, and a 3D vector, v (or s,v).
They correspond to the third line of the tetraktys (121), which, in binomial expansion form, is the numerical equivalent of a geometric 2D area: 1(2^0), 2(2^1), 1(2^2), because it consists of one center point, and two, orthogonal, dipoles, extending out from it, forming one quadrupole.
Increasing line 3 of the tetraktys to line four (1331) gives us a true 3D numerical equivalent of a geometric volume, which, as Hamilton’s friend Graves pointed out to him, could be formulated with seven imaginary numbers, but neither Hamilton nor Graves realized that these constructions, now called octonions, O, were in the true 3D level of the tetraktys, which we at the LRC now know is the numeric equivalent of the 2x2x2 stack of unit cubes, which we call Larson’s cube, containing one 2^0 point in the middle, three orthogonal dipoles, three orthogonal quadrupoles and one octopole, or 1(2^0), 3(2^1), 3(2^2), 1(2^3), in terms of the binomial expansion.
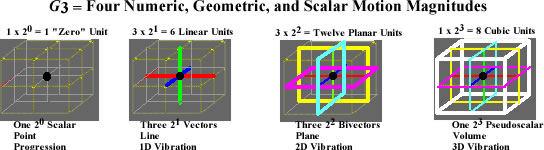
This is where the professor stomps his foot, because Baez and company apparently don’t recognize this. Instead they take the 8 corners of a 1x1x1 = 1 unit cube, not a 2x2x2 = 8 stack of 1-unit cubes, and they assign 7 of the 8 corners of the cube (poles) to the 7 imaginary numbers of Graves 9 (omitting the scalar a=1), and from this they devise a way to concoct the last remaining normed division algebra that can be constructed.

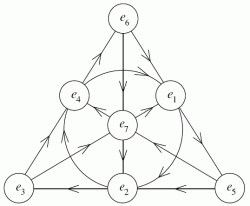
It’s complicated and a total distortion of the true nature of the tetraktys (they collapse their cube into a Fano plane.) This is not how we understand the tetraktys in terms of the binary expansion and its numerical equivalents of the geometric point, line, area and volume, forming Larson’s cube.
But what is very useful is the recognition that the four sums of the numbers of each the of the tetraktys, define the first four lines of Pascal’s triangle,
1 = 1
1+1 = 2
1+2+1 = 4
1+3+3+1 = 8
and which they call “dimensions,” limits the number of normed division algebras to these four geometric real dimensions, 0,1,2 and 3. This is the tetraktys and it contains all the geometric entities of our 3D universe, corresponding to the point, the line, the area and the volume. It’s a case of numbers confirming the first postulate of the RST, which states that everything consists of one component, existing in three dimensions (“Hear oh Israel, the Lord our God, the Lord is One.”)
Moreover, because of their mathematical concept of the single unit cube, with its 8 corners, defining the algebra of octonions, they assume that the next line of Pascal’s triangle (14641), leads to a fourth geometric dimension (24) in the form of the first hypercube, and they don’t stop there, but continue to higher dimensional hypercubes, collapsing them into a plane and studying their properties with group theory and Lie algebras.
To us, this is a grievous mistake, or at least unnecessary, not only because it misses the point of the identification of the binomial expansion with the magnitudes, dimensions and polarities of the tetraktys, geometrically expressed in the form of Larson’s cube, but also because it hides the real implications of Bott periodicity.
Baez explains Bott periodicity as the reason the number 8 is one of his three favorite numbers, but he can’t explain why this number is so significant, no one can, unless they admit that it reflects the fact that the physical universe is limited to three dimensions, geometrically speaking, as stated in the RST fundamental postulates.
If they would only admit this limitation, they would understand that lines 5 and up of Pascal’s triangle should be interpreted as compounds of line 4 of the triangle. In other words, lines 5 and up are multiples of the 3D line 4.
1) 1 = 1
2) 1+1 = 2
3) 1+2+1 = 4
4) 1+3+3+1 = (6+2) = 8
5) 2(1+3+3+1) = (12+4) = (1+4+6+4+1) = 16
6) 4(1+3+3+1) = (24+8) = (1+5+10+10+5+1) = 32
.
.
.
Thus, the true nature of Bott periodicity is seen in the scalar expansion of three dimensions in the form of Larson’s cube, which can best be understood as the linear expansion of a 1-unit dipole as the independent variable, with the 4 quadrupoles and 8 octopoles, as dependent variables.
Also, since two of the three dipoles and quadrupoles are degenerate in the nxnxn stack, we only need scale 1 each of them, as we go up each step of the triangle. Hence, starting with line 4 and renumbering, the Larson cube expands as:
1) 1^1(2^1) 1^2(2^2) 1^3(2^3) ~ 1 2x2x2 = 1dp, 1qp, 1op
2) 2^1(2^1) 2^2(2^2) 2^3(2^3) ~ 1 4x4x4 = 2dp, 4qp, 8op
3) 3^1(2^1) 3^2(2^2) 3^3(2^3) ~ 1 6x6x6 = 3dp, 9qp, 27op
4) 4^1(2^1) 4^2(2^2) 4^3(2^3) ~ 1 8x8x8 = 4dp, 16qp, 64op
.
.
.
We can see from this that the doubling of the sums of the steps in Pascal’s triangle, is due to the counting of the redundancy in the expansion of the 2x2x2 stack: there are ALWAYS 3 dipoles and 3 quadrupoles in the expanded stacks, so if we count all these entities, we get (counting just the number of entities, the bolded coefficients):
1) 1(2*0) + 3(2^1) + 3(2^2) + 1(2^3) = 8
2) 2(2*0) + 6(2^1) + 6(2^2) + 2(2^3) = 16
3) 4(2*0) + 12(2^1) + 12(2^2) + 4(2^3) = 32
.
.
.
Hence, we see clearly what has happened. The numbers in the expansion of Pascal’s triangle seem to be a reflection of the 3D expansion of Larson’s cube, not an n-dimensional expansion of a hypercube, as Baez and company see it.
Nevertheless, while the sums of the four 3D coefficients in the expansion of the initial LC (1331) match the sums of the successive lines in Pascal’s triangle, when they are doubled, the sums of the products of the coefficients with the respective n-dimensional entities do not match, except in line 4 (our line 1.)
1) 1(2^0) + 3(2^1) + 3(2^2) + 1(2^3) = 8 (27=27)
2) 2(2^0) + 6(2^1) + 6(2^2) + 2(2^3) = 16 (54 vs 81)
3) 4(2^0) + 12(2^1) + 12(2^2) + 4(2^3) = 32 (108 vs 243)
.
.
.
As explained in the previous post, to match the sums of the products, the coefficients of line 4 must be tripled in order to match the triangle, not doubled. So, to match the sum of the triangle’s coefficients (2n), we double the 3D coefficients, at each line (a power of 2), but to obtain the sum of the products of the coefficients and the n-dimensional entities, we have to triple the coefficients (a power of 3).
It’s weird, but it’s probably due to the fact that the coefficients contain the degeneracies of the dipoles (3) and quadrupoles (3) within the LC. To reconcile this conflict, we can use the triangle’s coefficients and the LC’s n-dimensional entities, even though we can’t identify them explicitly in a geometric figure, yet.
1x20, 3x21, 3x22, 1x23 = 1 + 6 + 12 + 8 = 27
1x20, 4x21, 6x22, 4x23, 1x(21x23) = 1 + 8 + 24 + 32 + 16 = 81
1x20, 5x21, 10x22, 10x23, 5x(21x23), 1x(22x23) = 1 + 10 + 40 + 80 + 80 + 32 = 243
1x20, 6x21, 15x22, 20x23, 15x(21x23), 6x(22x23), 1x(23x23) = 1+12+60+160+240+192+64 = 729
1x20, 7x21, 21x22, 35x23, 35x(21x23), 21x(22x23), 7x(23x23), 1x(21x23x23) = 1+14+84+280+560+672+448+128 = 2187
Notice, that we have broken down the terms with dimensions greater than three into subterms of dimension three or less, to respect the limits of Bott periodicity and the RST.
Even though it’s difficult to see how all these n-dimensional entities could possibly be assembled into one compound geometric figure, one thing is clear: The sum of the products of the triangle’s coefficients and the n-dimensionals of the cube are powers of 3, starting with the initial LC, 1331.*
Since we can now obtain the same result with the LC, we can re-write the expansion as:
LC0 = 33
LC1 = 3(LC0) = 34
LC2 = 3(LC1) = 35
LC3 = 3(LC2) = 36
LC4 = 3(LC3) = 37
which is a lot better than writing:
1x20, 3x21, 3x22, 1x23 = 1 + 6 + 12 + 8 = 27
3x20, 9x21, 9x22, 3x23 = 3 + 18 + 36 + 24 = 81
9x20, 27x21, 27x22, 9x23 = 9 + 54 + 108 + 72 = 243
27x20, 81x21, 81x22, 27x23 = 27 + 162 + 324 + 216 = 729
81x20, 243x21, 243x22, 81x23 = 81 + 486 + 972 + 648 = 2187
What the implications are of this clarification of scalar magnitudes, directions, and dimensions is hard to tell at this point, but my guess is that they are significant.
* Update: Turns out that this is not correct. I should have checked it. Please see my reply to Horace in the comments below.
Reader Comments (2)
I stop understanding your math at this paragraph:
Specifically at line 4: I do not understand why you choose to group 1+3+3+1 as (6+2) and why you chose to group 1+4+6+4+1 as (12+4) and not as (14+2)
Also, I don't understand why you wrote 2(1+3+3+1) = 1+4+6+4+1 instead of 2+6+6+2.
I know that 1+4+6+4+1 is the next line in binomial expansion but I do not see how it justifies fudging 2(1+3+3+1) and 1+4+6+4+1
Hi Horace,
Sorry, the problem is that I'm lazy. I should have spelled it out:
1) 1 = 1
2) 1+1 = 2
3) 1+2+1 = 4
4) 1+3+3+1 = (6+2) = 8
5) 2(1+3+3+1) = (2+6+6+2)=(12+4) = (1+4+6+4+1) = 16
6) 4(1+3+3+1) = (4+12+12+4)=(24+8) = (1+5+10+10+5+1) = 32
So, I'm just grouping like terms.
You wrote:
I'm trying to show that the sum of each line of the binomial expansion can be generated by doubling the previous line, and that this fact is important:
Line 5 = 2(line 4);
Line 6 = 2(line 5);
Line 7 = 2(line 6).
The trouble is, while doubling the previous line of the triangle, beginning with line 4, reproduces the sum of the binomial expansion, at each successive line, it does not produce the correct expansion of the tetraktys (T), with the sum of all its n-dimensional products. To get this, we have to triple the previous line, starting with line 4, which is shown symbolically as:
T0 = 3^3
T1 = 3(T0) = 3^4
T2 = 3(T1) = 3^5
T3 = 3(T2) = 3^6
T4 = 3(T3) = 3^7
What I should explain more is that treating the powers of 2 geometrically and mathematically, without making the distinction between them explicitly, leads to confusion.
We don't add points to lengths to areas to volumes, because it's like adding grapes to bananas to apples to oranges. However, if we treat points as monopoles (mp), lengths as dipoles (dp), areas as quadrupoles (qp) and volumes as octopoles (op), then we can add up all the poles in a given cube, and it makes sense.
The number of such poles in line 4 of Pascal's triangle, when we interpret it's numbers 1331 as coefficients of these poles, is 1mp + 3dp + 3qp + 1op = 1+6+12+8 = 27 poles. This is a power of 3 (3^3) and when we calculate the poles in line 5 of the triangle, with coefficients 14641 we get the 3^4 = 81 poles, and so on up the lines of the expanding triangle. We get the sequence of the powers of three: line 6 = 3^5, line 7 = 3^6, line 8 = 3^7, etc.
In fact, we don't have to use use the coefficients of the expanded triangle, we can just multiply the coefficients of line 4 by 3 and then sum the constituent poles to get the same result. For example, line 5 = 3(1331)=(3993)= 3mp+9dp+9qp+3op = 3+18+36+24 = 81 = 3^4 and so on.
Understanding it this way is important because it respects the 3D limitation of Euclidean geometry: the universe is 3D. Line 5 of the triangle is not 4D, because there is no such thing as 4 geometric dimensions. This explains a lot.
Ok, so while the sum of the numbers of each line of the expanded triangle is a power of 2, which we can express as multiples of 1331: 1331=8=2^3, 2(1331)=(2662)=2^4=16, 2(2662)=(4 12 12 4)=2^5=32, etc., the sum of the poles in each line of the expanded triangle is a power of 3, which we can also express as the geometric multiples of 1331: 1331=3^3=27 poles, 3(1331)=(3993)=3^4=81 poles, etc. (in this short hand way of showing it, of course.)
Understanding this much gives us the geometric insight that we need to see that what Baez et al are doing (and string theorists), by interpreting the lines of the expanded triangle as increasing geometric dimensions, in the form of hypercubes, is a grave error. The sums of these lines represent increasing mathematical dimensions (powers of 2), but not increasing geometric dimensions (powers of 3).
Now, the next thing we notice is that only portions of the expanded triangle follow the expanded LC's pattern, which is also a multiple of line 4, but expands as (2n+1)^3.
I am working on a new post about that now.
Update: When I say above that the doubling of the tetraktys does "not produce the correct expansion of the LC, with the sum of all its n-dimensional products," it is a misleading statement. Since the number of poles in a given expansion of the LC does not equal the number of poles in the corresponding expansion of the triangle anyway, this should refer to the pole numbers of the triangle, not the LC.
In other words, to get the correct number of poles in a given step of the triangle, using the 1331 numbers of the tetraktys, as the unit value, we have to triple it, not double it.
I have changed the LCs to Ts in this comment, but not yet in the original post.
Does this make sense?