Contemplating the Mystery of Unit Expansion
Unit progression, or expansion, is the central, core consequence of the RST. It is the starting point of the universe of motion, in every sense of the word. Larson developed the idea logically, and he maintained that his development was mathematically consistent, and he insisted that a new mathematical formulation was unnecessary.
In a letter to Frank Meyer, two years before he passed away. Larson wrote:
As I have tried to emphasize throughout my writings, the conceptual aspects of physical theory, our understanding of what the mathematics of physical events mean, is independent of the mathematical relations. There are usually many possible interpretations of the same mathematics. Consequently, the true meaning cannot be derived from the mathematics. As matters now stand, the accepted physical meaning of each mathematical relation is based on assumptions applicable to that particular case. Conventional physical theory has a general mathematical structure into which each individual conclusion is required to fit, but it has no similar conceptual structure, and it therefore has no way of verifying the conceptual interpretations of the mathematical relations. Our contribution is to provide the conceptual structure that is needed. Since the previous interpretations were based on unconnected assumptions, it was inevitable that some of them would turn out to be wrong, but this does not necessarily mean that the mathematical expressions are incorrect. And where we do find that some modification of the mathematical relations is necessary, we do not need any new kind of mathematics.
However, it is evident that “a new kind of mathematics” is necessary, since the legacy mathematics has taken a development route that follows vector motion, rather than scalar motion. In vector mathematics, as in vector motion, the point’s position, relative to another, is paramount, while in scalar mathematics, as in scalar motion, the magnitude’s value, relative to another, is paramount.
However, because a vector also has magnitude, confusion in terms of the mathematical meaning of scalar, since it has been understood mostly in the context of vector mathematics, results when we speak of scalar dimensions.
This confusion is cleared up when we cast scalar dimensions in the light of the first four levels of the binomial expansion, which yields the tetraktys (2^0 = 1, 2^1 = 2, 2^2 = 4, 2^3 = 8), since we can understand the base number 2 as two “directions” of a given dimension, which produces the doubling expansion 1, 2, 4 and 8 of poles, defining the geometry of Larson’s cube (point, line, plane and cube).
However, the fact that numbers, as factors, can be expanded without limit (n x 2; n—>∞), and the fact that mathematicians regard these factors as dimensions, has led them to regard factors of 2 greater than 3 as geometric dimensions (hyper geometric dimensions), even though a child can see that the logic is bogus.
It is a fact that nature stops at three dimensions, Raul Bott proved it, so trying to ignore that limit only leads to confusion, in the end, as we see it has in LST theory, which has been stopped dead in its tracks by it (see here.) While this was not so evident in Larson’s time, it is clear to almost everyone now: the trouble with physics is that physicists have sought solutions, by following mathematicians into the realm beyond three dimensions.
Here at the LRC, we not only assert that this is a mistake, we contend that there is no need to be tempted to do it, when one understands the science of simple mathematics in terms of the science of simple geometry.
When we expand Larson’s cube, the progression is 8, 64, 216, 512…(nx2)3, where n = 1, 2, 3, …∞. In this way, the base 2 increases not as factor of 2, but as a multiple of 2, and each dimension can be expanded in turn for each successive base:
(1x2)0 = 1; (1x2)1 = 2; (1x2)2 = 4; (1x2)3 = 8,
(2x2)0 = 1; (2x2)1 = 4; (2x2)2 = 16; (2x2)3 = 64,
(3x2)0 = 1; (3x2)1 = 6; (3x2)2 = 36; (3x2)3 = 216,
(4x2)0 = 1; (4x2)1 = 8; (4x2)2 = 64; (4x2)3 = 512.
Figure 1. Expansion of Larson’s Cube (LC).
This is scalar magnitude expansion in 0, 1, 2 and 3 dimensions. Each dimension has two “directions,” and the expansion proceeds step by step, as the natural, or counting numbers increase, according to the dimensional number of the term.
Since the expansion is eternal, picking a point in the count is tantamount to starting at the number one and increasing from there.
The unit number, 1, is the number 2 expanded from a point, 10, to a 2x2x2 = 8 stack of unit cubes, but all three dimensions, the line, the plane and the cube expand simultaneously in two “directions”, four “directions,” and eight “directions,” respectively (the point doesn’t expand, of course.) This gives rise to the numbers of the fourth line of Pascal’s triangle, 1331, which, when summed, equal 8.
This composite number, the tetraktys, or its geometric equivalent, the LC, can be understood as the 3D unit scalar and, if it is treated as such, it is clear that the subsequent lines of the expanded triangle are multiples of it, as we have already discussed in the previous post.
However, to treat the subsequent lines of the expanded triangle, line 5 and up, as 2n geometric dimensions, or as some kind of “extra” geometric dimension, is a grave error for physicists, who, we contend, must respect the limits of Euclidean geometry in their study of the structure of the physical universe, if they expect to progress.
Taking the binomial expansion of the tetraktys, the 2x2x2 = 23 = 8 unit cubes, and the corresponding 1mp+3dp+3qp+1op = 27 poles, as the fundamental scalar unit of our new system of mathematics, replacing the number 10, as the fundamental scalar unit, as understood in today’s mathematics, to which mathematicians then add “imaginary” numbers to this “real” number, in order to increase its dimensions, requires much of us to be sure, but it seems to me that it must be done, if we are to progress in our understanding of the physical universe.
All righty then.
Comparing the LC pseudoscalar expansion, 8, 64, 216, 512, …, to the triangle pseudoscalar expansion, 8, 16, 32, 64, …, it’s hard to see much of a correlation between the two. Whereas the sum of the numbers of a given line of the triangle is always equal to the pseudoscalar of that line, which is always a power of 2, and the sum of the number of poles of a given line is always equal to a power of 3, the sum of the number of poles of each successive LC expansion doesn’t follow this pattern, rather it follows a (2n+1)3 sequence: 33, 53, 73, etc.
So, while it’s easy to see that the tetraktys (1331) is a unit of the triangle and can be used to calculate its expansion, either the expansion of its numbers, or the expansion of their associated dimensions, when these are understood in the 3D terms of the tetraktys, the question now is, “Can we relate the tetraktys to the expansion of the LC, which has a different pseudoscalar than that of the triangle?”
Happily, the answer is yes. In fact, it is simple: We just need to join the tetraktys numbers with the dimensions of the LC expansion, as shown in figure 1 above, and voila, it appears:
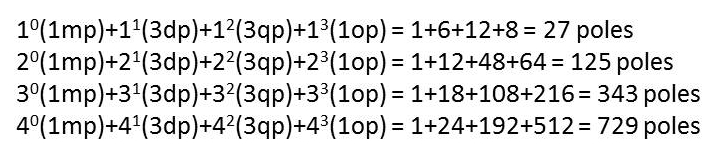
Figure 2. The Expansion of the Tetraktys and Larson’s Cube
There is much more work to do, but understanding how the dimensions of the tetraktys relate to the expansion of Pascal’s triangle AND the expansion of the LC and the implications of this for today’s mathematics and physics is a necessary step toward the development of a “new kind of mathematics.”
I think Larson would be happy, cautiously happy, but happy nonetheless.
Reader Comments