The Larson Research Center

In the discussion forum, there is reference to the excitement going on over at the rs2theory.org site due to the work of Miles Mathis.

Horace writes:

We have always been looking for the mathematical link between the magnitudes above and below one unit. Bruce uses the idea of projective geometry and counterspace to show how linear motion gets converted to reciprocal rotational motion below one unit (a.k.a. “crossing the unit boundary”). 
It looks like Miles Mathis has found another way:

Miles Mathis wrote:
I developed an equation to find one velocity from the other, using the radius r, and I later showed that at the size of the photon, a tangential velocity of c was equivalent to an orbital velocity of 1/c.
Source: http://milesmathis.com/charge3.html

This is good news indeed for those who have accepted the departure from the fundamental postulates of Larson’s RST, but for those of us unwilling to accept the argument that requires the abandonment of Euclidean geometry in favor of projective geometry, as the geometry of the universe of motion, and a concommitant change in the wording of the second fundamental postulate, not so much.

Not that the controversial work of Miles Mathis might not be valid, it might be, but it illustrates a fundamental misunderstanding in the mathematics of scalar motion that exists in the “RS2” community.

In their “re-evaluation of the Reciprocal System of Physical Theory,” the followers of the RS2 community have accepted the notion that the inverse of translational scalar motion in the material sector of Larson’s RSt appears to be rotational motion, from the point of view of the material sector and vice-versa: The inverse of translational scalar motion in the cosmic sector appears to be rotational from the point of view of the cosmic sector.

Consequently, crossing the boundary between the two sectors involves a transition from translational c-speed to rotational 1/c-speed, which Mathis has appeared to confirm in their minds with his work differentiating orbital and tangential speeds of photons.

However, in the LRC’s view, this approach confuses the fundamental concepts of scalar motion in the universe of motion, which are based on the principle of reciprocity, easily graphed as shown below:

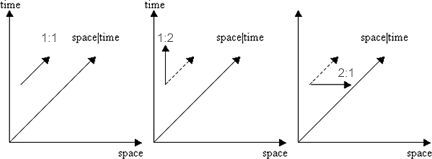
Figure 1. The Unit Boundary Between the Material and Cosmic Sectors of the Universe of Motion.

Just as 1/2 is the mathematical inverse of 2/1, Larson’s “direction” reversals in the unit space and time progression created two sectors of the universe of motion, by effectively stopping the progression of one or the other of the two reciprocal (hence orthogonal) components of the universal progression.

When the space component of an expanding location oscillates, changing the space:time progression ratio at that point from 1:1 to 1:2 (think of the increase of space as alternatingly increasing, decreasing, while the increase of time continues increasing normally), it effectively changes the progression at that point to a progression of time only, as shown in figure 1 above.

Conversly, when the time component of an expanding location oscillates, changing the space:time progression ratio at that point from 1:1 to 2:1 (think of the increase of time as alternatingly increasing, decreasing, while the increase of space continues increasing normally), it effectively changes the progression at that point to a progression of space only, as shown in figure 1 above.

This concept can be formulated mathematically by understanding that there are two interpretations of numbers: One represents quantity (how much or how many), the quantitative interpretation of number, while the other represents a relation between quantities, the operational interpretation of number.

The difference is readily understood when we consider the rational number line:

1/n, …1/3, 1/2, 1/1, 2/1, 3/1, …, n/1

The numbers to the left of unity, 1/1, are the inverse of the numbers to the right of unity. However, they may be interpreted both quantitatively and operationally, with different results, depending on the desired interpretation. Interpreted quantitatively, the numbers to the left of 1/1 are less than 1, or fractions of the whole, while the numbers to the right of 1/1 are multiples of 1.

On the other hand, interpreted operationally, the sets of numbers to the left and right of 1/1 are both multiples of 1: the set to the left are multiples of 1 in the opposite “direction” of that of the set to the right. The set to the right is the inverse of the set to the left, which changes the “direction” of its magnitudes, in the following sense:

1:n, …1:3, 1:2, 1:1, 2:1, 3:1, …, n:1

This is the sense of “direction” we have when comparing two quantities, as, for example, when we weigh quantities in a pan balance. There are three possibilites and only three: The pans are balanced with equal quantities on either side, or the pans are unbalanced with unequal quantities favoring one side or the other.

The oscillation of the space or time component at some given point in the 3D universal progression produces the discrete units of motion postulated in the first fundamental postulate of the RST. These discrete oscillating units of scalar motion may be algebraically combined and the relations between such combinations algebraically analyzed in a manner completely analogous to number systems that are well understood.

For instance, we can combine integer multiples of each:

1x(1:2) = 1:2         1x(2:1) = 2:1    
2x(1:2) = 2:4         2x(2:1) = 4:2
3x(1:2) = 3:6         3x(2:1) = 6:3
.                              .
.                              .
.                              .
nx(1:2) = n:2n        nx(2:1) = 2n:n

Clearly, in terms of magnitude and “direction,” these two sets of numbers are equivalent to opposites

-1, +1
-2, +2
-3, +3
.
.
.
-n, +n,

when quantitatively interpreted, but when operationally interpreted, they are multiplicative inverses, such that 1/n times n/1 = n/n, or unity.

When used to formulate speeds of the universe of motion, as we have illustrated in figure 1 above, we must make a distinction between material sector speeds and cosmic sector speeds, because one is speed-displacement from c-speed in terms of time, while the other is speed-displacement from c-speed in terms of space:

Material Sector                      Cosmic Sector

Δs/Δt = 1/1 = c                   Δt/Δs = 1/1 = c
Δs/Δt = 1/2 = 1Mc              Δt/Δs = 1/2 = 1Cc
Δs/Δt = 2/4 = 2Mc              Δt/Δs = 2/4 = 2Cc
.                                           .
.                                           .
.                                           .
Δs/Δt = n/2n = nMc                 Δt/Δs = n/2n = nCc

Where Mc = material speed-displacement = Cc = cosmic speed-displacement = 0.5c.

Of course, because these speeds are inverses, one is four times greater than the other, quantitatively, when considered from the reciprocal point of view (i.e. 2/1 = 4x0.5).

The attempt to quantify the RST concepts has led to different approaches, but the LRC was established to ensure that Larson’s fundamental postulates were not changed in the process. Opponents object to Larson’s idea of “direction” reversals and have sought to find an alternate way to obtain the required reciprocity of the system, by resorting to rotation. This is understandable, but the LRC takes exception to the concept of rotation as scalar motion.

Of course, the rejection of rotation as scalar motion means that the LRC departs from Larson’s development of the consequences of the RST in his RSt, but it does not imply departure from the RST itself, which must be held inviolate.

In its abandonment of the RST, it appears to us that the RS2 community has lost sight of the meaning of true reciprocity and in the attempt to justify its rationale, it now seems willing even to abandon the concept of scalar motion.