The Larson Research Center

Closure is something we all seek. Mathematically, it’s vital in order to successfully operate with numbers; i.e. to add, subtract and multiply and divide them consistently. Because the integers are closed under these mathematical operations, so too are the non-zero rationals.

However, the integer and rational number systems are actually composed of one dimensional numbers, or lengths. As we have discussed many times before, to deal with higher dimensional numbers, legacy system mathematics adds “imaginary” numbers to these number systems.

In the reciprocal system of mathematics (RSM), we recognize four scalar dimensions, with two “directions” each. At unit magnitude, these are isomorphic to the 4th degree of the binomial expansion, 20, 21, 22 and 23, which we call the tetraktys, because it consists of the first four numbers of the Pythagorean system of numbers: the monad, the dyad, the triad and the tetrad.

As we happily discovered some time ago, the binomial expansion of the tetraktys is the numerical equivalent of the geometry of the 2x2x2 stack of 8 unit cubes that we call Larson’s cube (LC). Its center, located where one corner of all 8 cubes coincide, defines the middle point of three, 1D, orthogonal lines, the intersection of three, 2D, orthogonal planes, as well as the intersection of the diagonals drawn between the eight reciprocal corners of the stack.

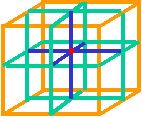
Figure 1. The Stack of Eight 1-unit Cubes Known as Larson’s Cube

The fact that this geometric figure contains the geometric representation of the four dimensions of the tetraktys and thus the first four binomial expansions of the tetraktys (counting zero), it follows that it also connects geometry with the eight mathematical dimensions of the four normed division algebras, the positive and negative reals, complexes, quaternions and octonions.

Moreover, the geometry of the LC not only represents the numbers of the tetraktys, it also defines a unit volume within its interior, and defines the inverse of this volume with its extent, a fact that connects the integer and rational numbers with irrational numbers, in a fundamental manner.

This connection between integers, rationals and irrationals provides a different approach to numbers and number systems that is not defined by Cantor’s sets nor Dedekind’s cuts, nor imaginary numbers. It is based on scalar expansion, where the three 1D lines, the three 2D planes and the eight 3D cubes expand outward from the 0D point.

Since a unit of space and a unit of time can be defined for the LC expansion, from point to cube, it follows that a unit of motion, v = Δs/Δt, can also be defined for it, and the inverse of the outward expansion, the unit inward motion of collapse. Since such a motion has only two possibilities, outward or inward, we can define them as the two scalar “directions” of motion, in contrast to the possible vector motion directions, which is a set of infinite directions.

Because these two scalar “directions” of motion, outward and inward, manifest themselves in each of the non-zero geometric components of the LC (the 1D line, the 2D area, the 3D volume), it’s easy to confuse them with the geometric “directions,” or poles associated with each of these entities, but we should note that the two poles of the 1D line can expand and contract, the four poles of the 2D area can expand and contract and the eight poles of the 3D volume can expand and contract.

Hence, we can use the base number 2 with non-zero exponents 1, 2 and 3 to represent the total “directions” of each non-zero dimension’s expansion, as indicated by the exponents: 21 = 2; 22 = 4, 23 = 8 “directions” respectively.

Given this isomorphism between the magnitude, dimension and “direction” of geometric expansion of the LC, and the magnitude, dimension and “direction” of the numerical expansion of the tetraktys, the question arises, “Can these geometric and numerical entities be used to form a number system that is closed under addition, subtraction, multiplication and division?” If the answer is “yes,” then it follows that the resulting 3D algebra will also have 2D, 1D, and 0D subalgebras that are closed as well.

While this may seem obvious given Clifford algebras, it isn’t, because the dimensions of the 3D Clifford algebra are used only to define the 1D (vector) space that the Clifford algebra operates in. Thus, it is all about the mathematical operations that translate and rotate vectors in that space.

In our case, we are dealing with an algebra of the spaces themselves. We seek to add and multiply LCs, if you will - the whole LC at once, represented by its geometric properties and the isomorphic numerical properties of the tetraktys.

As described in the previous entry, the numerical expansion of the LC, and thus the tetraktys, can be accomplished by addition or multiplication of its poles. Since the monopole, the three dipoles, the three quadrupoles and the single octopole comprise the unit and its subunits, they can be consistently manipulated algebraically.

To demonstrate this requires only that the geometric coefficients (1331) of the four-part numbers (1(20)+3(21)+3(22)+1(23)) be removed, before the algebraic operation is performed, and then reinserted into the number after the calculation is complete. For example, we can show that this works for addition, subtraction, multiplication and division, by letting the unit LC equal ‘a.’ Then,

a = (1+2+4+8)

b = 2a = 2 x (1+2+4+8) = (2+4+8+16)

c = 3a = 3 x (1+2+4+8) = (3+6+12+24)

d = 4a = 4 x (1+2+4+8) = (4+8+16+32)

Next we perform the following operations:

For multiplication,

1) a/b x c/d = ac/bd
   ((1+2+4+8)/(2+4+8+16)) x ((3+6+12+24)/(4+8+16+32)) =
   ((1+2+4+8)(3+6+12+24)/((2+4+8+16)(4+8+16+32)) =
   ((3+12+48+192)/(8+32+128+512)) =
   ((3(1+4+16+64))/(8(1+4+16+64))  = 3(1+2+4+8)2/8(1+2+4+8)2 = 3/8

 Just as a/2a x 3a/4a = a(3a)/(2a)(4a) = (3a2)/(8a2) = 3/8

For addition,

2) a/b+c/d = ad+bc/bd = 

    (1+2+4+8)/(2+4+8+16) + (3+6+12+24)/(4+8+16+32) =
    ((1+2+4+8)(4+8+16+32) + (2+4+8+16)(3+6+12+24))/((2+4+8+16)(4+8+16+32)) =
    ((4+16+64+256)+(6+24+96+384))/(8+32+128+512) =
    (10+40+160+640)/(8+32+128+512) =
    10(1+4+16+64)/8(1+4+16+64) =
    10(1+2+4+8)2/8(1+2+4+8)2 = 5/4

Just as

(a/2a)+(3a/4a) = ((a x 4a)+(2a x 3a))/(2a x 4a) = 10a2/8a2 = 10/8 = 5/4

And finally, for division,

3) (a/b)/(c/d) = (ad)/(bc) =
    ((1+2+4+8)/(2+4+8+16))/((3+6+12+24)/(4+8+16+32)) =
    ((1+2+4+8)(4+8+16+32))/((2+4+8+16)(3+6+12+24)] =
    (4+16+64+256)/(6+24+96+384) =
    4(1+4+16+64)/6(1+4+16+64) = 4(1+2+4+8)2/6(1+2+4+8)2 = 2/3 

Just as 

(a/2a)/(3a/4a) = (a(4a))/((2a)(3a)) = (4a2)/(6a2) = 2/3

Of course, since a = 1, 2/3 = 2a/3a = 2(1+2+4+8)/3(1+2+4+8) or, equivalently, 2(20+21+22+23)/3(20+21+22+23)

With the calculation complete, we insert the geometric numbers (1331) back into the final terms, which gives us the correct number of poles. For instance, in this last example,

2(20+3(21)+3(22)+23) = (2+12+24+16) = 54

3(20+3(21)+3(22)+23) = (3+18+36+24) = 81

54/81 = 2/3.

But then, why not just use the number of poles in the LC to begin with?

LCp = (1x(20)+3x(21)+3x(22)+1x(23)) = (1+6+12+8) = 27,

and since 27 = 33, then let

a = 33
b = 2(33)
c = 3(33)
d = 4(33)

and naturally, the algebra is still closed under addition and multiplication.