Toward a New Multi-Dimensional Scalar Number System
I’ve played around with number systems in the LRC’s New Math blog for years, but until a recent email exchange with my daughter Michele, I had not given it much thought for some time.
To my dismay, however, I started thinking about it again and, now, I cannot get it out of my mind. Readers of the blog might recall how one of my favorite topics in mathematics is how math, employed in theoretical physics, has developed historically.
I like to start with Sir William Hamilton and his discovery and fascination with quaternions (see here.) I first learned about it from David Hestenes, who more or less resurrected the idea of quaternions, in connection with his work on his Geometric Algebra.
Not being a mathematician, or even one inclined to the subject, my interest was driven by the implications of scalar motion, which seemed to me to be almost, if not entirely neglected by everyone except Dewey Larson and his followers.
Just before the disagreement within ISUS drove me to organize the LRC, I had given some thought to expressing the fundamental ideas of Larson numerically. I had this idea that the numbers 1/2, 1/1, 2/1 could be used to quantify the RST concepts of material and cosmic sector space and time displacements, as defined by Larson.
But soon, I realized that these one-dimensional numbers, if they were to be useful to express scalar motion entities, would have to be extended to multi-dimensional numbers, and this eventually led me to understand the great disconnect in modern number systems, as mathematicians tried to understand how to extend non-scalar motion, or vector motion, to multi-dimensions.
Ironically enough, it was Hamilton’s discovery of quaternions that led the way to the derailment, even though it was he who complained most eloquently about the use of so-called imaginary numbers, which eventually were to enable him to form quaternions, ironically enough. However, this use of imaginary numbers to increase the dimensions of ordinary, or scalar numbers, has led to pathological algebras, which I’ve talked about many times (e.g. see here.)
The fact is, only the algebra of one-dimensional numbers is non-pathological. The two-dimensional complex numbers lose the order property of scalar algebra, while the three-dimensional quaternions lose both the order property and the commutative property, and the octonians, which would be four-dimensional numbers, add associativity to the lost properties of multi-dimensional numbers.
Of course, if we consider scalars as zero-dimensional numbers, then complex numbers would be one-dimensional, quaternions would be two-dimensional and octonions would be three-dimensional, which would help clear up the understanding of non-mathematicians, with a geometric perspective, letting them relate the number systems to the corresponding geometrical concepts of point, line, area and volume.
However, the mathematicians look at numbers as algebraic operators, and they like to designate their dimensions in those terms, so an algebraic expression of complex numbers, with two terms, z = (a + bi), for example, is considered two-dimensional, and an expression of quaternions, with four terms, H = (a+bi+cj+dk), is considered four-dimensional, and one of octonions, with eight terms, a scalar number and seven imaginary numbers, is considered eight-dimensional.
Thus, unfortunately, the dimensions of algebra, lose their direct correlation with the dimensions of geometry, among the mathematicians. Nevertheless, we were able to show how the dimensions of numbers are indeed correlated with the dimensions of geometry, when viewed through the tetraktys and Larson’s Cube (e.g. see here.)
With all this as prelude, we come to the core of this blog entry: What can replace the multi-dimensional vector aglebra of today’s number systems, based on imaginary numbers? The answer is a multi-dimensional scalar algebra, based on ratio, which is the mathematical corollary to motion. In the set of zero-dimensional numbers, correlated with geometric points, the members of the set are the familiar rationals called integers and their inverses:
1/n, …1/3, 1/2, 1/1, 2/1, 3/1…, n/1
We can say that this set is based on multiples of the scalar unit 10 = 1, but what about a higher dimensional set based on multiples of the linear unit 11? What would its members look like? Or a set based on multiples of the square unit 12? What would its members look like? Or a set based on multiples of the cube unit 13?
The problem is that, in algebra, 10 = 11 = 12 = 13= 1 = (1x1) = (1x1x1), while in geometry, a unit point is a zero dimensional magnitude (10), differentiated from a unit line, which is a one-dimensional magnitude (11), differentiated from a unit area, which is a two-dimensional magnitude (12), and differentiated from a unit volume, which is a three-dimensional magnitude (13).
These multi-dimensional, geometric entities are not algebraically inter-operable. How do you multiply or divide a line times an area, or a point times a volume, or how do you add and subtract them from one another? You can’t, because the geometric dimensions of these units differ, while the dimensions, represented by the exponents in the corresponding algebra are not even dimensions in the same sense.
Unlike geometric dimensions, where each dimension is an orthogonal magnitude, the algebraic dimensions are not orthogonal magnitudes, but simply denote a number of factors in the expression of a mathematical operation.
However, if we recognize this difference, we can change the meaning of the exponents, so that:
0D = 10 = unit point
1D = 11/2= unit line
2D = 21/2 = unit area
3D = 31/2 = unit volume
This may appear to be a strange suggestion, but there is a way to employ these multi-dimensional numerical units, as geometric units, by utilizing a geometric theorem: the theorem of Pathagoras. Thus, given
n = 1, 2, 3, …, ∞,
Unit point = (12)1/2;
Unit line = (n2)1/2;
Unit area = (n2 + n2)1/2;
Unit volume = (n2 + n2 + n2)1/2.
On this basis, the members of the 0D scalar set, based on unit point numbers, are noted as before:
1) 1/n, …1/3, 1/2, 1/1, 2/1, 3/1…, n/1,
But the members of the 1D linear set, based on unit line numbers, are:
2) 1/n(12)1/2, …1/3(12)1/2, 1/2(12)1/2, (12)1/2/(12)1/2, 2(12)1/2/1, 3(12)1/2/1…, n(12)1/2/1.
The members of the 2D square set, based on unit area numbers, are:
1) 1/(n2+n2)1/2, …1/(32+32)1/2, 1/(22+22)1/2, (12+12)1/2/(12+12)1/2, (22+22)1/2/1, (32+32)1/2/1…, (n2+n2)1/2/1.
The members of the 3D cube set, based on unit cube numbers, are:
1) 1/(n2+n2+n2)1/2, …1/(32+32+32)1/2, 1/(22+22+22)1/2, (12+12+12)1/2/(12+12+12)1/2,(22+22+22)1/2/1, (32+32+32)1/2/1…, (n2+n2+n2)1/2/1.
If these multi-dimensional number sets turn out to have the properties required for mathematical groups, then their members should be able to be algebraically manipulated, with no pathology in the higher dimensions, as is now found in the higher dimensions of the legacy number system, based on imaginary numbers.
Some of the group properties are easily seen in the new sets. For instance, the identity element of all of them is equal to 1, which implies that multiplication by it will not change a member of the set. Also, a member of the set, when multiplied by its inverse is equal to 1. I think all the other group properties should hold as well, but I haven’t tested them to see.
For example, in the 2D case, the second element multiplied by its inverse element is:
Given x = sqrt(n), written in the form of the Pathagorean theorem, then:
(x)*(1/(x)) =
sqrt(2)*(1/(sqrt(2))) =
(12+12)1/2 * (1/(12+12)1/2 = ((12+12)1/2)/((12+12)1/2) = 1
Now, when each element is divided by its inverse, the 1D elements are squared, giving us the progression series,
1) e/(1/e) = e2 = 1, 2, 3, …n2,
while the 2D elements divided by their inverses produce the progression series:
2) e/(1/e) = e2 = 2, 8, 18, …2(n2),
and then the 3D elements divided by their inverses, produce the progression series
3) e/(1/e) = e2 = 3, 12, 27, …3(n2)
We can visualize these multi-dimensional, geometric numbers graphically, by drawing the unit ball inside the Larson cube, which just contains it, and drawing a second ball that just contains Larson’s cube. Taking a 2D slice of the 3D result, we get the graphic of figure 1 below:
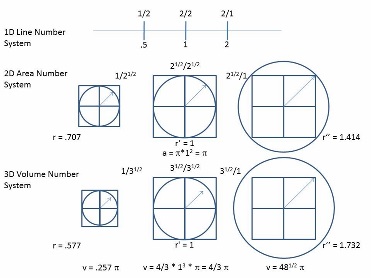 Figure 1.
Figure 1.
Note that the graphic of figure 1 does not illustrate the 1D linear number system in Larson’s cube, as it does the 2D and 3D systems. This is because I did not understand at the time I first made the graphic that, just as our RSt here at the LRC differs from Larson’s RSt, in that it BEGINS with 3D entities, the 3D oscillations of SUDRs and TUDRs, rather than with the 1D entities, the 1D oscillations of photons, with which Larson’s RSt begins, so too should our new number systems.
We can do this by writing one system equation, with three values of n: n1, n2, n3, in the 3D equation of the Pathagorean theorem, as follows:
e/(1/e) = e2 = ((n12 + n22 + n32)1/2)/(1/((n12 + n22 + n32)1/2),
where n2 and n3 = 0, for the 1D system,
and n3 = 0, for the 2D system.
The result is the three progression series, 1(n2), 2(n2) and 3(n2), shown above in 1), 2) and 3), respectively, for sucessive values of n1, n2 and n3.
While this simplification of the current multi-dimensional number system that is based on imaginary numbers (i.e. the square root of -1), may not appear to be relevant, at this point, to a civilization that has managed to construct the marvels of modern science and mathematics, building upon this imaginary foundation, we must remember that the theoretical physics community cannot complete it’s explanation of reality on this basis, given that quantum mechanics and general relativity are fundamentally incompatible.
It must be recognized that the dimensions of the fundamental energy equation, E = mc2, are the dimensions of inverse motion and that it follows that this fact cannot be ignored in light of our thesis that the universe consists of nothing but motion and its inverse.
This is especially clear, given Xavier Borg’s demonstration that the true physical dimensions of all physical units are the dimensions of motion (sn/tn) and inverse motion (tn/sn), where n = 0, 1, 2 or 3. Thus, the mass energy equation can be written in terms of these dimensions of motion and its inverse,
E=mc2 =
(t/s) = (t3/s3)x(s2/t2),
and the radiation energy equation can also be written in these terms, when the frequency term is recognized as just a convenient measure of vibration, clarifying the dimensions of Planck’s constant, s2/t, the dimensions of the so-called “quantum of action,” which dimensions are simply an ad-hoc compensation, derived to compensate for the use of the non-physical, but mathematical expression of the frequency term, 1/t. Making this correction, the radiative energy equation is simplified to,
E=hv =
(t/s) = (t2/s2)x(s/t).
However, treatment of physical equations such as these, and their implications, will be handled in our New Physics blog. For our purposes here in the New Math blog, it is sufficient to reform the number systems and their associated algebras, for application to the new physics.
Reader Comments