The Larson Research Center

Exploring the scalar properties of the tetraktys, we are exploring fundamental concepts of magnitude, dimension and “direction.” In the last post, we saw that the numerical expansion of what we call Larson’s cube (LC), which is the geometric equivalent of the tetraktys, can be expressed as:

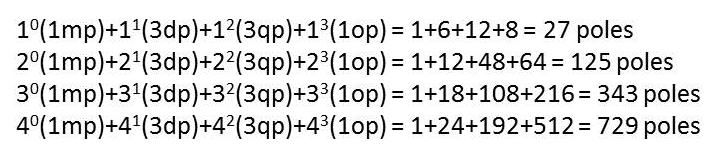
where poles are the constituent components of monopoles (mp=1), dipoles (dp=2), quadrupoles (qp=4) and octopoles (op=8). This gives us a means to express the sum of the unlike dimensions of unit numbers: In other words, we can sum the unit points, the unit areas, and the unit volumes of elements of the expanded tetraktys (1331), which is the numerical equivalent of the expanded LC, in terms of these poles.

Consequently, the numerical expression of the scalar expansion of the LC is

33, 53, 73, …(2n+1)3, n = 1, 2, 3, …∞

Now, it’s important to distinguish between this 3D expansion of the tetraktys and the 0D expansion of Pascal’s triangle, or the binomial expansion, which is normally considered as the numerical expansion of geometric dimensions, without including the notion of magnitude and “direction.” The scalar expansion of the triangle is simply,

20, 21, 22, 23, …2n, n = 0, 1, 2, 3, …∞

We can interpret this expansion as the expansion of the countable number of points:

20 = 1 instance of 1 point; 21 = 2 instances of 1 point; 22 = 2 sets of 2 instances of 1 point; 23 = 2 sets of 2 sets of 2 instances of 1 point, etc.

1) 20 = (*) = 1
2) 21 = (*)+(*) = 1+1 = 2
3) 22 = [(*)+(*)]+[(*)+(*)] = 2+2 = 4
4) 23 = {[(*)+(*)]+[(*)+(*)]}+{[(*)+(*)]+[(*)+(*)]} = 4+4 = 8

Hence, unlike the numerical expansion of the tetraktys, which is equivalent to the 3D geometric expansion of the LC, the numerical pattern of the triangle is not equivalent to any geometric expansion, but it is simply a regrouping of 0D terms. Take line four for example:

4) 23 = {[(*)+(*)]+[(*)+(*)]}+{[(*)+(*)]+[(*)+(*)]} = 4+4 = (*)+(***)+(***)+(*) = 1+3+3+1 = 8

That this sum of points in line 4 of the triangle (4+4 = 8) is equal to the sum of dimensional coefficients in the tetraktys (1+3+3+1 = 8) appears to be the cause of a colossal error in the development of mathematics: The fundamental confusion resulting from an incorrect understanding of magnitude, dimension and “direction” in mathematics and geometry, is tantamount to a detour along the road to comprehending their unity.

As a result of this non-comprehension, mathematics has been developed along a non-geometric line, leading to the confusion in the theory of algebra lamented by Hamilton, wherein he observed:

…it requires no peculiar scepticism to doubt, or even to disbelieve, the doctrine of Negatives and Imaginaries, when set forth (as it has commonly been) with principles like these: that a greater magnitude may be subtracted from a less, and that the remainder is less than nothing; that two negative numbers, or numbers denoting magnitudes each less than nothing, may be multiplied the one by the other, and that the product will be a positive number, or a number denoting a magnitude greater than nothing; and that although the square of a number, or the product obtained by multiplying that number by itself, is therefore always positive, whether the number be positive or negative, yet that numbers, called imaginary, can be found or conceived or determined, and operated on by all the rules of positive and negative numbers, as if they were subject to those rules, although they have negative squares, and must therefore be supposed to be themselves neither positive nor negative, nor yet null numbers, so that the magnitudes which they are supposed to denote can neither be greater than nothing, nor less than nothing, nor even equal to nothing. It must be hard to found a Science on such grounds as these, though the forms of logic may build up from them a symmetrical system of expressions, and a practical art may be learned of rightly applying useful rules which seem to depend upon them. 

 The effect of this detour probably only appears to the non-genuises (Hamilton was truly a genuis) among us, when we seek to understand the properties of scalar motion. After all, who needs to understand n-dimensional scalars in the practical world of vector motion?

In the theoretical world of nothing but motion, we have to combine n-dimensional entities of motion and determine how these combos relate to one another. We can’t do it without first clearing up the confusion in our understanding of these fundamentals.

Hopefully, it’s getting to the point that we can begin to formulate the n-dimensional, scalar algebra we need to move forward, though the very idea must appear preposterous and nonsensical to the uninitiated.