The New Physics
Do Faster-Than-Light Neutrinos Invalidate Einstein's E = mc^2?
The iconoclastic discovery of faster-than-light neutrinos, if confirmed, again places the Reciprocal System of Physical Theory (RST) in the lime-light. Or at least it would, if the new system weren’t ignored by the Legacy System of Physical Theory (LST) community.
Here at the Larson Research Center (LRC), we are getting woefully behind major new developments, as they come in ever faster. Nevertheless, it’s interesting to see how the RST easily accommodates the new superluminal neutrino findings. In our preon model of the LST standard model of particle physics, we can see that there are two of every fermion particle and anti-particle, except neutinos.
For instance, a left-handed and a right-handed version of the negative electron, and the two corresponding versions of the positive electron (positron), occupy the left and right end positions in the LRC schematic, as shown in figure 1 below:
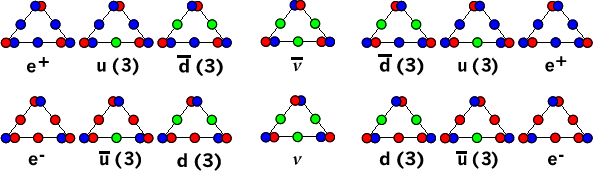
Figure 1. LRC Chart of Standard Model Fermions Based on SUDR|TUDR Triplet Combos
From this chart, we can see that the central positions of the neutrino and anti-neutrino are unique in that, like the fulcrum of a lever, they are in-between the left and right sides of the chart. This means that, if we rotate the chart horizontally, the positions of all the particles are swapped, except those of the neutrinos, which maintain their central positions along the axis of rotation.
However, notice that such a rotation will invert the postions of the constituent preons (S|T units) in every particle of the chart, including those of the neutrino and anti-neutrino, so that the S|T units on the left and right sides of each triangle are swapped and the left - right orientation of the bottom S|T units in the triangles is reversed.
Thus, the two sides of the chart, the front and backsides if you will, represent two, reciprocal, sets of S|T combos, which correspond to the two sectors of the RST universe of motion. Hence, there are actually two neutrinos and two anti-neutrinos in the system, which Larson would have designated the m-neutrino and the c-neutrino, together with their corresponding anti-particles, inhabiting their respective material and cosmic sectors of the universe of motion.
Therefore, we see that the constituent S|T combos of each sector of the universe of motion exhibit a “handedness,” or chirality, as it is called, which is an observed property of the respective fermions. Of course, the LST standard model also includes a description of interactions between these constituent particles. These interactions are described in terms of mediating particles called bosons, which are the photons, the W and Z bosons and the gluons, together with the missing Higgs boson.
While we have been concentrating our study mostly on the fermions at the LRC, it should be noted that particle interactions in the universe of motion must be described in terms of motion, rather than in the terms of the autonomous “forces,” which the LST community has concocted to suit their purposes, and that this necessarily includes the interaction between the material sector (constructed of material fermions) and the cosmic sector (constructed of cosmic fermions).
Such material sector|cosmic sector interactions are rare, occuring only at the boundaries of the two sectors, where vector motion in space approaches the speed of light, which is the unit speed of the scalar universal space/time expansion.
In the material sector, the 3D oscillations of the SUDRs (space-like motion of fundamental constituents of material fermions) necessarily consist of less-than-speed of light motion, from the expansion of space, or the Material Sector, point of view, while the 3D oscillations of the TUDRs (time-like motion of fundamental constitutents of the cosmic fermions) necessarily consist of less-than-the-speed of light motion, from the expansion of time, or Cosmic Sector, point of view.
With this much understood, the observed faster-than-light neutrinos, if confirmed, would be explained in the RST community, in general, as a sector boundary phenomena, where the time component of c-neutrinos, moving through material sector matter, are “sling-shotted” along their way by the time component of space-like oscillations of the m-fermions. The SUDRs of these fermions have two units of time expansion, for every unit of space expansion, making them less-than-the-speed of light entities, from the space expansion point of view, but effectively increasing the speed of c-neutrinos by their uniform time expansion.
This interaction amounts to the c-neutrinos hitching a ride on the time expansion of m-fermions (i.e. the c-neutrino takes advantage of the m-fermion’s space oscillations, when passing through them,) which is tantamount to effectively increasing their speed, from the expansion of space (material sector) point of view.
Relative to the unit expansion, then, the c-neutrinos are moving faster, like a man running forward on the top of a moving train, from the material point of view, even though they would be moving slower, like a manning running backward on the top of a moving train, from the cosmic point of view.
The bottom line is that Einstein’s equations remain valid, within each sector, but motion in time (space), viewed from across the sector boundary, appears to violate the universal speed limit, just as the inverse of a rational number appears to be greater or smaller, depending upon one’s point of view. Put another way, if the left end of an East-West aligned teeter-totter is lower than its right end, as viewed from its South side, the reverse will be true, when it is viewed from its North side.
The trouble with LST physics, however, is that they do not understand that there are two, reciprocal, sectors of the universe: There is one where matter is constructed of fermions with more less-than-the-speed-of-light material SUDRs, the oscillations of which are space-like, and one where cosmic matter is constructed with more less-than-the-speed-of-light cosmic TUDRs, the oscillations of which are time-like.
But they’re getting there…
The Other Half
The 3D model of the S|T unit is a composite of two 3D oscillations, the space oscillation, the SUDR, and the time oscillation, the TUDR. Since they are the inverse of each other, the SUDR is 27 times smaller than the TUDR. We can therefore use the SUDR volume, surface or radius to express the relationship numerically. For example, let’s use the volume:
54(1/27)/(27), (27(1/27)/(27), (27(1/27)/2(27), or(54/27)/27, 27/27, 27/54
As explained in the previous entry, only the unit measure of 3 volumes out of the lower 27, actually cube to an integer. 9, 18 and 27, which enables us to use them as 1/3, 2/3 and 3/3 of the whole, in 3D terms. Interestingly enough, however, in 1D terms, the numbers are different. Only three SUDR radii fit in a TUDR radius (i.e. 3 * (1/31/2) = 31/2), so the volume sum in which the SUDR radius is 1/3, 2/3 and 3/3 of the TUDR radius is 1, 8 and 27, respectively. I will defer the discussion of the ramifications of this fact until later. Right now I want to complete the other half of the numeric system, where the SUDR is larger than the TUDR, what we can refer to as the upper half of the number system, which terminates at 54/27.
Figure 1 below shows the chart of the upper half that corresponds to the chart of the lower half provided in the previous entry.
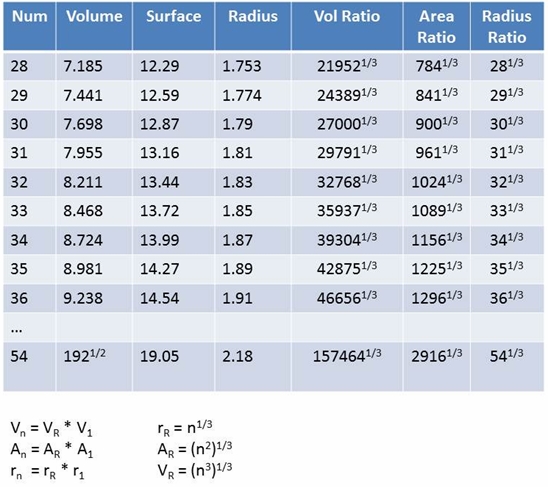
Figure 1. Chart of 27 SUDR Volumes Summing to Two TUDR Volumes
The concepts being introduced here are somewhat subtle. First, we assume that our universe is nothing but motion, with two reciprocal aspects, space and time, existing in discrete units. Since nothing is perfect, we must introduce a deviation into the perfect, one for one, expansion of space and time. The only deviation possible is a “direction” reversal in one of the two aspects, which produces a unit displacement in the otherwise perfect expansion.
We label the unit space displacement, SUDR, for space unit displacement ratio, and the unit time displacement, TUDR, for time unit displacement ratio. In simple terms the SUDR is a 3D space oscillation, while the TUDR is the inverse of this, a 3D time oscillation.
These two fundamental units progress, or increase, in their respective non-oscillating aspects. For the SUDR, this means that for each half of its oscillation, time continues to expand, and for the TUDR, space continues to expand, during each half of its oscillation. If we chart these motions we see that they are perpendicularly oriented, because they are reciprocals. Hence, it is possible that the time expansion of a space oscillation (SUDR) could bring it into contact with the space expansion of a time oscillation (TUDR).
A combination of these two fundamental entities constitutes a new ratio of space and time, a SUDR|TUDR (S|T) unit. A little consideration will show that an S|T unit is an oscillating combination that propagates in both space and time, and therefore can come into contact with other instances of S|T units, forming compound units. Consequently, we need to calculate the properties of this fundamental scalar motion combo in order to explore the possible combinations that might occur and then compare them to observations.
From simple geometric and mathematical properties, we deduce that the radius of the smallest TUDR is the square root of 3, and that the radius of the largest SUDR is the inverse of this, which means that, while it is three times smaller than the radius of the TUDR, its volume is exactly 27 times smaller than the volume of the TUDR.
Of course, these sizes are all relative until we choose a unit for the scale, which undoubtedly must be based on the speed of light.
The 3D Preon Model
As I have already admitted, to my chagrin, I was trying to build the LRC’s preon model using the 2D square root of 2-based number system, but I couldn’t get there. When I realized my mistake, I started over, using the correct 3D square root of 3-based number system, but now I had to deal with a very disconcerting challenge: Whereas the volume of the incorrect 2D TUDR was eight times the volume of the incorrect 2D SUDR, the volume of the correct 3D TUDR is 27 times the volume of the correct 3D SUDR!
True, the preon model was doable with these numbers (based on 3), but only if certain volumes were selected, the volumes of 9, 18 and 27 SUDR sums. While this meant that the radius of the TUDR (31/2) was three times the radius of the SUDR (1/31/2), so that the color charges of the quarks and the electrical charges of the electron and positron and the neutrality of the neutrinos worked out, as they should, the thirds were divided up into 3*9=27 increments of volume, each additional SUDR adding only a fraction of the required third!
For a day or two, this seemed to me to be a fatal flaw, but today I’m happy to report the discovery of what surely must be the answer: If we divide each increment of volume by its inverse and then cube that value, the only increments that come out as integers are 9, 18 and 27! All other volume increments are not integers. They are all irrational numbers. What this means, I believe, is that all volume increments except these three are excluded from forming combinations with their reciprocal counterparts by the discrete postulate of the RST. Happy day!
Readers can test this assertion themselves using the chart in figure 1 below:
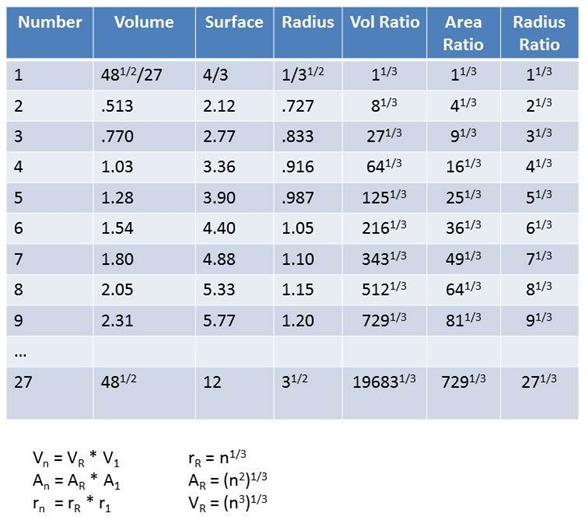
Figure 1. Chart of 27 SUDR Volumes Summing to One TUDR Volume.
The values in the volume, area and radii columns are mostly rounded off irrational numbers, so the respective ratios must be used to get the actual numbers. This is done by multiplying the indicated ratio by its respective value in the column of the initial SUDR (row 1). The rounded off values in each row can then be used as an approximate value to check to ensure that the correct value has been calculated.
For example, for the ninth volume, we multiply the cube root of 9 by the inverse of the square root of 3, which gives us the radius for the ninth volume. Then, squaring the radius and cubing it, gives us the integer 3. Doing the same thing for number 18 yields the integer 12, while it yields the number 27 for n = 27.
As far as I can tell, no other n than these three meets the requirement.
Whew!!
The Other Famous Equation of Theoretical Physics
Yesterday, I showed how the most famous equation in theoretical physics, E = mc2, fits like a glove into the LRC’s development of its RST-based theory of fundamental physics. In a universe of nothing but motion, mass, energy, charge, magnetic moment, quantum spin, etc, the nature of which are unexplainable in the LST framework, must be identified as scalar motions. They are either scalar motions, combinations of scalar motions, or relations between these.
Since we now see that the most famous equation of theoretical physics can be explained in terms of n-dimensional scalar motion, it’s natural to ask if the other famous equation of physics, perhaps the second most famous equation, can also be explained in terms of scalar motion. This is the equation
E = hv,
where E is energy, h is Planck’s constant and v is the frequency of light. This equation is central to the LST community’s theory of quantum physics, because it defines the quantum of energy that all material things are built upon. It is the fundamental equation of the universe of matter.
Of course, it must also be the fundamental energy equation of the RST community’s work as well, but here it has to be understood in terms of n-dimensional scalar motion; that is, in terms of fundamental units of space and time, not in terms of the LST’s concept of “action” and 2π rotation, as in the LST-based theory.
It was Larson who insisted that the LST dimensions of h, the dimensions of action, were unphysical. In Chapter 12 of Nothing But Motion, he argued:
In all of the space-time expressions of physical quantities [derived in this work], the dimensions of the denominator of the fraction are either equal to or greater than the dimensions of the numerator. This is another result of the discrete unit postulate, which prevents any interactions from being carried beyond the unit level. Addition of speed displacement to motion in space reduces the speeds; the atomic rotation can take place only in the negative scalar direction, and so on. The same principle applies to the dimensions of physical quantities, and the dimensions of the numerator of the space-time expression of any real physical quantity cannot be greater than those of the denominator. Purely mathematical relations that violate this principle can, of course, be constructed, but according to the theoretical findings they have no real physical significance.
…
The most notable of the quantities excluded by this dimensional principle is “action.” This is the product of energy, t/s, and time t, and in space-time terms it is t²/s. Thus it is not admissible as a real physical quantity. In view of the prominent place which it occupies in some physical areas, this conclusion that it has no actual physical significance may come as quite a surprise, but the explanation can be seen if we examine the most familiar of the conventional applications of action: its use in the expression of Planck’s constant. The equation connecting the energy of radiation with the frequency is
E = hv
where h is Planck’s constant. In order to be dimensionally consistent with the other quantities in the equation this constant must be expressed in terms of action.
It is clear, however, from the explanation of the nature of the photon of radiation that was developed in Chapter 4, that the so-called “frequency” is actually a speed. It can be expressed as a frequency only because the space that is involved is always a unit magnitude. In reality, the space dimension belongs with the frequency, not with the Planck constant. When it is thus transferred, the remaining dimensions of the constant are t²/s², which are the dimensions of momentum, and are the reversing dimensions that are required to convert speed s/t to energy t/s. In space-time terms, the equation for the energy of radiation is
t/s = t²/s² x s/t
Of course, Larson speaks in terms of his concept of “scalar rotation,” a speed concept that we have replaced with the concept of 3D oscillation, but the relation of 1D, 2D and 3D scalar motion in the equation remains the same. If we write Larson’s version of the energy equation in terms of the ratio of the 1D diameters, 2D surfaces and 3D volumes of the fundamental S|T unit, the SUDR|TUDR combination, we get:
Td/Sd = Ta/Sa * Sd/Td,
where, again, T and S designate the TUDR and SUDR and d, a and v are their diameter, area and volume dimensions. With π factored out, this gives us four times the radius squared for the 2D area, and twice the radius for the 1D diameter (see here),
2(r”)/2(r) = 4(r”2)/4(r2) * 2(r)/2(r”),
2(1.732)/2(.577) = 4(1.7322/(4(.5772) * 2(.577)/2(1.732),
3 = 9 * .333…
3 = 3
If we think of 1D oscillation as the cube root of 3D oscillation, then we can re-write the last term of the equation as
(Sv/Tv)1/3 = (.257/481/2)1/3 = .333…
even though 1D oscillation isn’t defined independently in our work, as it is in Larson’s. The reason why only one dimension of the oscillation is effective in the equation, instead of two or three dimensions, still remains to be explained. However, I suspect that it has to do with the direction of propagation of the light, which can only be detected in one dimension at a time.
At any rate, these are exciting times.
More Clues and Corrections
In the last entry I made a big mistake, using the radius of the square root of 2 and its inverse to calculate the minimum volume of the TUDR and the maximum volume of the SUDR. Whether it was because I was fixated on the “that damn number,” 2/9, or because I confused the 2D view of Larson’s Cube (LC) with the actual 3D stack of cubes, I don’t know, but for some reason I spaced it out and, though I caught it, my readers quickly did too.
I was highly concerned, however, fearing that what seemed to be working out so well with the square root of 2 radius, would no longer be so promising, with the square root of 3 radius. I dreaded re-doing the calculations that I had worked out for the periodic table, but since I couldn’t see how those calculations related to preon model of particles, I had some hope that the new calculations would fit both.
Yet, I found that, while I could fit the square root of 2 based numbers into the pattern of the periodic table quite nicely, but not into the preon model of particles, the square root of 3 numbers did fit the preon model quite nicely!
I suspect that this is a clue that the numerical pattern of the periodic table is based on 2D properties of scalar motion combos, while the preon model is based on the 3D properties of their constituent motions. This makes sense, because the 3D oscillations contain all the lower dimensional oscillations as well, and both our atomic model and photon model are 3D oscillations. A triple combination of 3D S|T units can have a 2D configuration topologically, a triangle, if the S and T units are not coincident, while the double combination can only have a 1D configuration, a line, under these assumptions.
However, I don’t know if it can be maintained that the two aspects of motion ought to be separated to any degree, by space or time, since the separation, if any, would have to be a separation of motion (i.e. space and time), and motion not participating in the oscillations at that.
But regardless, we actually have three different sets of radii to work with: First, we have the center radius, which is the product of the two inverse radii that is always equal to 1, designated radius r’, the radius of the inner sphere contained inside the LC (technically a ball).
On the right of the unit sphere, we have the radius of the outer sphere containing the LC, designated r”. On the left, we have the inverse of the outer sphere, obtained by constructing a second, smaller, LC, just contained by the unit sphere. This third radius is designated r.
In the 2D case, the third dimension does not exist, so the spheres are flattened to circles, with magnitude in the plane of the x and y axes only, but in the 3D case, the two inverse radii are actually diagonals of a cube and therefore have an x, y and z component. The magnitude of the largest, with its radius designated r”, corresponds to the radius of the TUDR. It is the square root of 3, while the radius of the SUDR, designated r, is the inverse of the square root of 3. The three sets of lengths are shown in the figure below, depicted as different number systems:
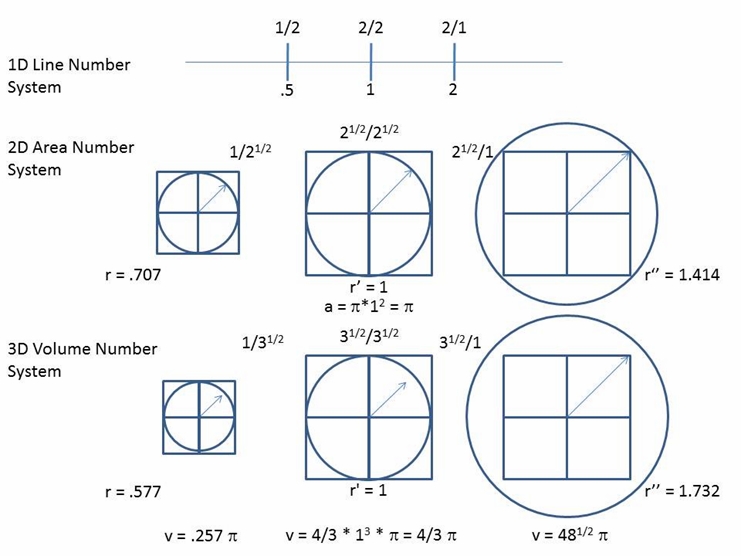
Figure 1. The 1D, 2D, and 3D sets of lengths (radii) contained in the SUDR and TUDR
The idea is that the 2D and 3D number systems, based on units of the square root of 2 and the square root of 3, respectively, are isomorphic to the familiar 1D number system, all things considered. That is to say, the ratios 1n/2n, 2n/2n, and 2n/1n, where n equals the appropriate dimensional unit, constitute a valid number system in each case.
However, the 2D system subsumes the 1D system and the 3D system subsumes them both. Hence, the 3D system is a composite of 0D, 1D, 2D and 3D numbers. Surprisingly, however, the ratios of the various numbers contained in the reciprocal components of the composite form a pattern of integers that corresponds to physical patterns based on 0, 1, 2 and 3 dimensions, as well.
The most fundamental aspect of the system is the reciprocity of the larger numbers on the right, the smallest 0D number of which is r”, and the smaller numbers on the left, the largest 0D number of which is r. Recall that the continuous magnitudes of the circles and spheres are constrained by the discrete magnitudes of the squares and cubes of the LC and vice-versa. Each circle, or sphere, has a set of four squares, or 8 cubes of sequential sizes between it and the next circle or sphere.
As the discrete, right, lines of the LC expands, the 0D numbers (unit lengths) progress, 1, 2, 3, 4, …, the 1D numbers (side lengths of stack) progress, 2, 4, 6, 8, …, the 2D numbers (faces of stack) progress, 4, 16, 36, 64, while 3D numbers (# of cubes in stack) progress, 8, 64, 216, 512, ….
At the same time, the outer circle, sphere, containing the squares, cubes, expands, delineated by the increasing 0D diagonal radii, 21/2, 81/2, 181/2, 321/2, the increasing 2D surface, 8, 32, 72, 128, …, and the increasing 3D volume, 481/2, 30721/2, 349921/2, 1966081/2, ….
As figure 1 indicates, each of these n-dimensional numbers in the 3D expansion has it’s inverse. The question now is, “What does all this mean, physically, if anything?”
To tell the truth, there is so much popping out that I seem to have a tiger by the tail. There is a growing set of rational numbers emerging from all this that, like a set of Legos, can be used to build many wonderful things, but I want to share one, new, and unexpected, clue, which in particular intrigues me. Consider the following equation,
Td/Sd = Tv/Sv * Sa/Ta,
2(r”)/2(r) = 481/2/.257 * ((4/3)/12)
3 = 27 * .111…
3 = 3
Where T and S designate TUDR and SUDR respectively, and d, v and a are 1D diameter, 2D area, and 3d voluume designators, respectively. Of course, it turns out that the dimensions are the same as those in the famous equation:
E = mc2
which, in space/time terms, is written:
t/s = t3/s3 * s2/t2
Maybe this is just a happy coincidence. Maybe it’s nothing new, but please feel free to inform me, if so, because I missed it before, somehow.