The New Mathematics
Eighth Post in the BAUT RST Forum
The eighth post in the BAUT forum follows. These posts are a continuation of the RST thread in the “Against the Mainstream” forum of BAUT.
+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
(continued from previous post)
What I have done, in answering antoniseb’s question, seeking to understand the context in which Larson’s RST is applicable to physics, is to show that a new, operationally interpreted, view of the numbers in this hypercomplex structure, reveals that there is an astonishing simplicity existing in it, when it is expressed in terms of “non-rotatable” (i.e. non-vector), but nevertheless n-dimensional, scalar numbers, called “Reciprocal Numbers” (RNs).
The power of the RNs should be clearly manifest in this, because, on the one hand, Baez asserts that, referring to the perplexing structure of hypercomplex numbers where n < 3, “You can classify all these things,” but when n is equal to, or greater than, 3, then the classification breaks down, because “3-dimensional manifolds are a lot more complicated: nobody knows how to classify them; 4-dimensional manifolds are a lot more complicated: you can prove that it’s impossible to classify them - that’s called Markov’s Theorem.”
Yet on the other hand, we can show that they are easily classified, in the new system of reciprocal numbers. The first four dimensions (counting the zero dimension) are classified by the first four RNs:
- 20 (1/1) = 1/1
- 21 (1/2+1/1+2/1) = 4/4
- 22 (4/8+4/4+8/4) = 16/16
- 23 (16/32+16/16+32/16) = 64/64
where
- = RN0
- = RN1
- = RN2
- = RN3
The next four dimensions are then:
- 24 (1/1) = 256/256
- 25 (256/512 + 256/256 + 512/256) = 1024/1024
- 26 (1024/2048 + 1024/1024 + 2048/1024) = 4096/4096
- 27 (4096/8192 + 4096/4096 + 8192/4096) = 16384/16384
where
- = RN4
- = RN5
- = RN6
- = RN7
and so on, up the ladder of dimensions, ad infinitum. We can see the structure more clearly when the ascending powers of the RNs are expanded in terms of the powers of the first RN:
- = (1/2+1/1+2/1)0 = 1/1
- = (1/2+1/1+2/1)1 = 4/4
- = (1/2+1/1+2/1)2 = 16/16
- = (1/2+1/1+2/1)3 = 64/64
- = (1/2+1/1+2/1)4 = 256/256
- = (1/2+1/1+2/1)5 = 1024/1024
- = (1/2+1/1+2/1)6 = 4048/4048
- = (1/2+1/1+2/1)7 = 16384/16384
The reason for the mysterious connection of Bott periodicity and the rotation groups that mathematicians work with in topology, is that, as Raul Bott proved, there are no new phenomena beyond three geometric dimensions in nature. However, as we can now see, that applies to the vectorial aspect of the structure only, it does not apply to the scalar aspect.
From the scalar point of view of n-dimensional numbers, the Bott periodicity theorem’s assertion that there is a limit at three dimensions, after which things repeat, is clearly seen when we factor out the value of 24 = 256 from the RNs in each group. This shows us that each 3D group is based on powers of 256:
2560
- 20 (1/1) = 1/1
- 21 (1/2+1/1+2/1) = 4/4
- 22 (4/8+4/4+8/4) = 16/16
- 23 (16/32+16/16+32/16) = 64/64
2561
- 20 (1/1) = 1/1
- 21 (1/2+1/1+2/1) = 4/4
- 22 (4/8+4/4+8/4) = 16/16
- 23 (16/32+16/16+32/16) = 64/64
2562
- 20 (1/1) = 1/1
- 21 (1/2+1/1+2/1) = 4/4
- 22 (4/8+4/4+8/4) = 16/16
- 23 (16/32+16/16+32/16) = 64/64
.
.
256n
- 20 (1/1) = 1/1
- 21 (1/2+1/1+2/1) = 4/4
- 22 (4/8+4/4+8/4) = 16/16
- 23 (16/32+16/16+32/16) = 64/64
which is why Bott’s period 8 periodicity theorem holds.
It is the lack of recognition, on the part of the physicists, of the nature of space, as the reciprocal aspect of time, in scalar motion, together with the lack of recognition, on the part of the mathematicians, of the operational interpretation of rational numbers, as integers, that is the root cause of the present confusion, both physical and mathematical.
What we have discovered is that the vectorial science is related to the scalar science; that is, vectorial science emerges from scalar science, just as vectors emerge from scalars. The key is to understand and recognize that the duality of numbers is built in, it doesn’t have to be an add on through an ad hoc invention such as imaginary numbers.
The contribution that Hestenes has made, in bringing to light the advantage of using Clifford algebras in dealing with vectors, extends beyond the utilitarian aspect, regarding the use of different approaches to vector science, and ultimately lies in the unification of vectorial and scalar mathematical concepts.
However, this is not clear until the reciprocal ideas of Larson are applied to numbers, as well as space and time, and this is accomplished through following Hestenes’ example in exploiting the idea of the operational interpretation of number. For this reason, the value of Hestenes’ work is not fully appreciated yet, because the focus has been on GA defined as a better language for vectorial physics, not as a generalization of the number concept to accommodate the magnitude concept.
This is why Baez observes:
| Differential topology is the study of smooth manifolds, emphasizing questions of a topological flavor, but concentrating on *smooth* (i.e., infinitely differentiable) rather than *continuous* functions between manifolds. Differential geometry is also the study of smooth manifolds, but emphasizing questions of a geometrical nature. Differential geometry is the mathematics used in general relativity, gauge theory and so on - - it’s basic to a lot of modern physics. Naturally it has a lot of ties to differential topology. In principle, geometric algebra is the study of algebraic structures related to geometry, such as Lie groups, Lie algebras, Grassmann algebras, Clifford algebras, and so on. In practice, it often refers to the program of David Hestenes and his disciples, who seem to think Clifford algebras are the center of the mathematical universe, and show a Procrustean tendency to force everything into a Clifford algebra framework. One should beware of this or any other form of idolization of a particular mathematical gadget at the expense of others. It leads to narrow-mindedness. However, all the algebraic gadgets I listed above are important in differential topology and differential geometry, and in this sense, learning geometric algebra is an important part of learning those other subjects. |
In other words, the fact that the 3D dimensions of the octonions makes for a great way to do 2D physics, is greatly eclipsed by the fact that they make it possible to do 3D, or scalar, physics!
What we want to show next is how, even though restricted to integers, nature provides us with a continuum, and how that union actually exists in an integer number system like the RSM, reflecting Kronecker’s astute observation:
| God made the integers, all else is the work of man. |
Excal
Seventh Post in the BAUT RST Forum
The seventh post in the BAUT forum follows. These posts are a continuation of the RST thread in the “Against the Mainstream” forum of BAUT.
+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
Hmmm. I’m not sure how to interpret the silence. I know this is primarily an astrophysics/cosmology forum, but the science of astrophysics and cosmology rests on the foundation of particle physics. The whole idea of big bang, cosmic inflation, nucleosynthesis, etc, is developed on the basis of the standard model and general relativity theories, so these fundamental sorts of things are hopefully seen as vital here. Again, the trouble with physics right now is that these two theories must be treated separately, as if the quantum and the continuum were unrelated, though we know that they are not, and this conflict emerges most clearly in today’s concepts of cosmology and astrophysics.
However, to make my point a little more explicit and to explain things a little further, I’ll refer to John Baez’s characterization of Geoffrey Dixion’s work in Week 59 of his online mathematics tutorials:
| Originally Posted by Baez Dixon is convinced that the details of the Standard Model of particle interactions can be understood better by taking certain mathematical structures very seriously. There are very few algebras over the reals where we can divide by nonzero elements: if we demand associativity and commutativity, just the reals themselves and the complex numbers. If we drop the demand for commutativity, we also get a 4-dimensional algebra called the quaternions, invented by Hamilton. If in addition we drop the demand for associativity, and ask only that our algebra be “alternative”, we also get an 8-dimensional algebra called the octonions, or Cayley numbers. (I’ll say what “alternative” means in “week61”.) Clearly these are very special structures, and also clearly they play an important role in physics… or do they? |
| …there are not too many places in physics yet where the octonions reach out and grab one with the force the reals, complexes, and quaternions do. But they are certainly out there, they have a certain beauty to them, and they are the natural stopping-point of a certain finite sequence of structures, so it is natural for people of a certain temperament to believe that they are there for a reason. Dixon makes a passionate case for this in the beginning of his book. |
| The octonions show up in many contexts in superstring theory, but few would say this theory is “based” on the octonions. A better description might be that string theorists are forced into using special algebraic structures to get things to work, and these special structures have an unnerving habit of being related to the octonions. Of course, this is far more interesting than if they’d *set out* to incorporate the octonions into their work. Geoffrey Dixon has an extension of the Standard Model which makes use of all four normed division algebras: reals, complexes, quaternions and octonions: Geoffrey M. Dixon, Division Algebras: Octonions, Quaternions, Complex Numbers and the Algebraic Design of Physics, Kluwer, Dordrecht, 1994. Not enough people have looked at this stuff carefully, but if one does, one finds interesting relations to the SU(5) and SO(10) grand unified theories, which show how the patterns underlying the symmetry breaking in these theories are related to division algebras. Sometime I’d like to write about this. You can read more about Dixon’s ideas here: http://www.7stones.com/Homepage/Alge…/algebra0.html There is also a bit more lurking in my seminar notes on Clifford algebras, spinors, the Standard Model and the SU(5) grand unified theory: http://www.math.ucr.edu/home/baez/qg-spring2003/ though I didn’t manage to cover enough of the really cool stuff. |
The main mathematical challenge of this structure is best described by the loss of its elements’ properties, as the dimension of the hypercomplex numbers increases; that is, in the words of one commentator on Baez’s site:
| The real numbers are *not* of characteristic 2, so the complex numbers don’t equal their own conjugates, so the quaternions aren’t commutative, so the octonions aren’t associative, so the hexadecanions aren’t a division algebra. |
In Week 211, Baez writes:
| Bott periodicity is all about how math and physics in n+8-dimensional space resemble math and physics in n-dimensional space. It’s a weird and wonderful pattern that you’d never guess without doing some calculations. It shows up in many guises, which turn out to all be related. The simplest one to verify is the pattern of Clifford algebras. |
| Originally Posted by “John Baez” There are some spooky facts in mathematics that you’d never guess in a million years… only when someone carefully works them out do they become clear. One of them is called “Bott periodicity”. A 0-dimensional manifold is pretty dull: just a bunch of points. 1-dimensional manifolds are not much more varied: the only possibilities are the circle and the line, and things you get by taking a union of a bunch of circles and lines. 2-dimensional manifolds are more interesting, but still pretty tame: you’ve got your n-holed tori, your projective plane, your Klein bottle, variations on these with extra handles, and some more related things if you allow your manifold to go on forever, like the plane, or the plane with a bunch of handles added (possibly infinitely many!), and so on…. You can classify all these things. 3-dimensional manifolds are a lot more complicated: nobody knows how to classify them. 4-dimensional manifolds are a lot more complicated: you can prove that it’s impossible to classify them - that’s called Markov’s Theorem. Now, you probably wouldn’t have guessed that a lot of things start getting simpler when you get up around dimension 5. Not everything, just some things. You still can’t classify manifolds in these high dimensions, but if you make a bunch of simplifying assumptions you sort of can, in ways that don’t work in lower dimensions. Weird, huh? But that’s another story. Bott periodicity is different. It says that when you get up to 8 dimensions, a bunch of things are a whole lot like in 0 dimensions! And when you get up to dimension 9, a bunch of things are a lot like they were in dimension 1. And so on - a bunch of stuff keeps repeating with period 8 as you climb the ladder of dimensions. (Actually, I have this kooky theory that perhaps part of the reason topology reaches a certain peak of complexity in dimension 4 is that the number 4 is halfway between 0 and 8, topology being simplest in dimension 0. Maybe this is even why physics likes to be in 4 dimensions! But this is a whole other crazy digression and I will restrain myself here.) |
Sixth Post in the BAUT RST Forum
The sixth post in the BAUT forum follows. These posts are a continuation of the RST thread in the “Against the Mainstream” forum of BAUT.
+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
Since reciprocal numbers (RNs) are composed of OI numbers, and OI numbers are isomorphic to integers, they do not have the property of direction. However, they do have the property of “direction,” because just as an increasing negative integer increases in the opposite “direction” with respect to increasing positive integers, an increasing OI number on one side of unity increases in the opposite direction with respect to increasing OI numbers on the other side of unity. Thus, 1/2 + 1/2 = 2/4 = -2 is “farther away” from unity than 1/2 = -1, but in the opposite “direction” with respect to unity than a similar increase on the positive side of unity would be.
However, given two RNs such as, for example,
(1/2 + 1/1 + 2/1) = 4/4 and (2/4 + 2/2 + 4/2) = 8/8,
there is no orthogonal relationship of directions that can be defined when combining them, just as there is no orthogonal relationship of directions that is definable when physical scalars such as points, or pseudoscalars such as volumes, are combined. Consequently, when multiplying RNs, though we multiply each term in the multiplicand by each term in the multiplier, as we would if they were vector magnitudes, the product “n times m” literally means that n is repeated m times, not that the scalar unit is changed to an “n by m” area unit by the operation. Also because the numbers are OI numbers, not fractions, we multiply numerators by numerators and denominators by denominators in each term, so the product of the two RNs is
(1/2 + 1/1 + 2/1) * (2/4 + 2/2 + 4/2) =
(4/4) * (8/8) = 32/32 nm,
because multiplying three terms by three terms,
(1/2 + 1/1 + 2/1)
(2/4 + 2/2 + 4/2) =
2/8 + 2/4 + 4/4 + 2/4 + 2/2 + 4/2 + 4/4 + 4/2 + 8/2,
gives us nine terms. Then, combining like terms together, we get
(2/8 + 2/4 + 2/4) + (4/4 + 2/2 + 4/4) + (4/2 + 4/2 + 8/2) =
[(6/16) + (10/10) + (16/6)] = 32/32 nm,
but the result is a scalar number, not a vector; that is, we are multiplying points here (actually pseudopoints, because RNs have volume). This means, in the language of GA, that the multiplication operation doesn’t affect the grade of the pseudoscalar, or 3-blade, anymore than it affects the grade of the scalar, or 0-blade.
So, while a vector times a vector is a bivector, a higher grade blade, and a vector times a bivector is a trivector, a higher grade blade, a scalar times a scalar is a blade of the same grade. Stating the same thing symbollically,
A1* B1 = C2 (in the form of the “sum” of the inner and outer product, the geometric product), and
A1 * B2 = C3,
for the vectors, and
A0 * B0 = C0 ,
for the scalars, but what’s suprising is that
C3 * C3 = C3, not C9
for the pseudoscalars! This is because the three dimensions of the pseudoscalar are the internal dimensions of the volume, represented by the three terms of the RN, and the nine terms of the product are always just scalar expansions of their three terms, as I have shown above.
As far as I know, this has never been noted before, because GA isn’t designed to use the 3-blades, except as what is called the unit trivector, symbolized by the upper case letter, I. This view of the trivector is a vector view, but it is also called a pseudoscalar, because its outer product commutes with everything, as a scalar does. Yet, unlike a scalar, it also changes sign under inversion! What does that remind you of?
What we have discovered here is that the dilation of the scalar, or origin of a coordinate system, in the form of the pseudoscalar, can be expressed in the usual terms of the three dimensions of vectors, as a trivector, or alternatively, in terms of the three “dimensions” of the RNs, as a pseudoscalar. Moreover, this leads us to view the binomial expansion, which is the dimensional expansion of duality, as the expansion of points, which don’t expand; the expansion of vectors which expand vectorially, and the expansion of pseudoscalars, which expand scalarly. That is why the numbers down the left and right edge of Pascal’s triangle are always 1, but the numbers between these two are always more than 1, but also always symmetric.
However, there is a difference between the 1s down the left side, which are scalars (20 = 1), because they have no direction, but magnitude only, and the 1s down the right side, which are pseudoscalars (2n), because they have all directions possible in n dimensions. Hence, the number of directions in the pseudoscalar is the same as the number in the scalar at n = 0, namely zero, but at n = 1, the number of pseudoscalar directions is two, represented by the scalar expansion in all the directions of a line from the perspective of the scalar point in the middle (linear dilation). At n = 2, the number of pseudoscalar directions is four, represented by the scalar expansion in all the directions of a plane from the perspective of the scalar point in the middle (quadratic dilation), and at n= 3, the number of pseudoscalar directions is eight, represented by the scalar expansion in all the directions of a cube from the perspective of the scalar point in the middle (bi-quadratic dilation), as clearly depicted in Larson’s Cube.
There is much more to say about all this, but suffice it to say for now, that these are concrete mathematical results that are the subject of the mathematical research at the LRC. The application of these scalar math concepts, in developing a suitable language for the LRC’s scalar physics research, is a major goal of the LRC. The prospect of using the new language effectively is promising, given that string theory, the standard model’s guage theories, and the fundamentals of group theory and symmetry principles, all converge to the same place: the space of the octonions.
It has long been suspected that the octonions have a deep connection with physics for many reasons, but so far the connection has escaped physicists. Now that there is a new kid on the block, though, things may change relatively quickly. Our first objective is to understand the RSM, and we’ve made a lot of progress since first discovering it. Yet, none of this means anything, unless we can connect it to observations. We have hints on how to do that with photons of radiation, but our primary goal is to use the RNs to find the properties of neutrinos, electrons, positrons, protons, and neutrons, and learn how they relate to each other, and to photons, in the atomic spectra.
If we can do that, we will be on our way, because the origin of the material properties of mass, charge, and spin, are unexplainable in vector physics, but they should be relatively easy to explain in scalar physics, where the three “dimensions” of RNs, correspond to outward motion in space, outward motion in time, and inward motion in space, or in time, the magnitudes of which are functions of events and their associated probabilities.
Thus, since forces, such as gravitational, electrical, and magnetic forces, are properties of motion, we expect to discover how they are related to the three dimensions of motion in the RNs. An exciting prospect, indeed.
I guess this concludes my long-winded initial answer to antoniseb’s question. If there are followup questions, I would be happy to try to answer them.
Fifth Post in the BAUT RST Forum
The fifth post in the BAUT forum follows. These posts are a continuation of the RST thread in the “Against the Mainstream” forum of BAUT.
+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
Larson gave us very few diagrams to illustrate the principles of scalar motion, but in the previous posts, I introduced an algorithm, called the progression algorithm (PA), that produces a visual output that is very helpful in studying the scalar space/time progression ratio. The unit progression PA is
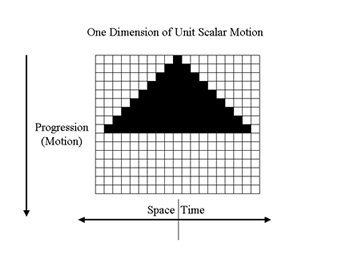
Figure 1. Unit Space/Time Progression PA
The unit progression is the datum, the point of reference for the scalar motion of the universe of motion, the apeiron, the perfect symmetry of the Reciprocal System’s initial state, the space/time ratio equal to a 1/1 space/time progression. We call it the natural reference system of motion, the physical “zero” of the system, from which all physical activity is measured in the RST, and we use the PA in figure 1 above to generate this state of scalar motion as the unit progression ratio of space/time.
In the previous posts of this thread, I’ve explained how the symmetry of this initial state is spontaneously broken by “direction” reversals in the uniform progression of the space or time aspects of the motion, producing a second state of the system that deviates from the natural reference system by one unit in one of two possible “directions,” one of which is designated “negative” and the other “positive.” The PAs in figures 2 and 3 below generate these two progression ratios.
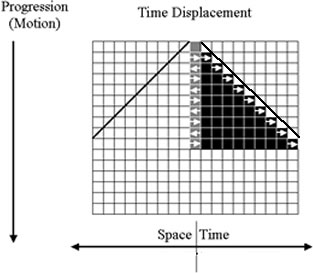
Figure 2. The Unit Time Displacement PA
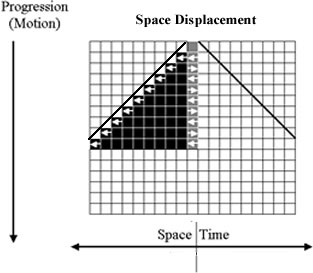
Figure 3. The Unit Space Displacement PA
These two units of magnitude exist on either side of the unit ratio, and, taken together, the three of them correspond exactly to the initial three numbers of the integer number system, generated by the operational interpretation of the magnitude of rational numbers. In fact, we can easily summarize all this information with just a few numbers. The three numbers:
1/2, 1/1, 2/1,
which, operationally interpreted, are equivalent to three integers
-1, 0, +1,
because the change in the rates of progression of space and time, caused by the “direction” reversals in one aspect or the other, confines the progression of the oscillating aspect of the progression to be confined to one unit. In scalar physics, then we have a process, “direction” reversals, that, given a unit space/time progression, ds/dt = 1/1, producees two new ratios, ds/dt = 1/2 and ds/dt = 2/1, which constitute discrete, unit, magnitudes of oscillations, or motion, the peiron, emerging from the apeiron.
Now, one of the first things we want to know is, “What can we do with these numbers?” We want to know if we can add, subtract, multiply, divide, raise their powers, and extract their roots, because, if we can, then we have an algebra of scalar motion, and it will go a long way towards helping us develop a scalar science around the scalar system.
Larson was asked, many times, if there were a new mathematical formalism to go with his new system, and he insisted that there wasn’t, because there wasn’t any need for one, that the primary contribution of the RST is a clarification of the concepts of motion, not an addition to the already vast field of mathematics.
However, we now see the mathematics of a new system of numbers emerging from the mathematical equivalent of the RST assumptions. Whereas, in the RST, we assume that one component, motion, with two reciprocal aspects, space and time, is the initial condition of the physical universe, in the RSM, we assume that one number, an operationally interpreted ratio, with two reciprocal aspects, numerator and denominator, is the initial number of the mathematical universe.
Given this operational interpretation of the ratio of integers, as a signed integer itself, several things happen. First, we remove the necessity of qualifying zero as a number, which of course, it isn’t. Zero is an important concept in its own right, to be sure, but it isn’t a number. At least now it isn’t. Second, we have no need to use signs with OI numbers, where the number itself is unique, and unambiguous. Third, we have no concept of orthogonality. The dimensions of OI numbers cannot include the notion of multiplication in the sense of magnitudes that are the product of two, orthogonal magnitudes of direction, because OI numbers are scalar numbers, and scalar numbers do not have direction, or othogonality.
However, given their equivalence to integers, we already know a lot about how they constitute a mathematical field and all, because they are isomorphic to the integers; that is,
1/n, …, 1/2, 1/1, 2/1, …, n/1,
is isomorphic to
-x, …, -1, 0, 1, …, x,
so anything we know about the integers, holds for the OI numbers, as well.
Therefore, if we add 1/2 = -1, to 2/4 = -2, we get 3/6 = -3, and, in general, m/n + m/n = 2m/2n, and so on.
Nevertheless, there is a big difference when we add equal OI numbers on opposite sides of unity, because not only are they equal in magnitude, but they are inverses as well. Therefore, like equal weights on the opposite sides of a pan balance, they balance each other, they do not eliminate one another. For example, a one pound weight on one side of a balance exactly offsets an equal weight on the opposite side, but together they weigh two pounds. In contrast, with integer numbers, a negative number cancels an equal positive number, requiring the concept of zero, the bane of modern theoretical physics.
Hence, we when we add 1/2 + 2/1, we get 3/3 = 1/1, not zero, but the operation is isomorphic to -1 + 1 = 0. It’s just a different animal. Now, since n/n = 1/1, then
2/2 + 2/2 = 4/4 = 1/1,
a balanced OI number. Nevertheless, in the case of the ds/dt = 1/2 case of the time displaced PA, for every two units of time progression there are still two units of space progression, the difference being that one of these two space units is an increase (arrow points to the left), and one is a decrease (arrow points to the right). Thus, if we add the respective numbers of the two unit displaced PAs, we get
(1/2 + 2/1) = 3/3,
because we have not counted the decreasing space unit (arrow to the right) on the time displaced PA, nor the decreasing time unit (arrow to the left) on the space displaced PA. Adding a term to account for these units, gives us
(1/2 + 1/1 + 2/1) = 4/4 nm,
where “nm” is the unit of “natural motion.” This equation is a fundamental equation of the RSM, and is called the first, reciprocal, number (RN) of the RSM. Again, given that we are assuming that the OI number system is isomorphic to the integer number system, the RN, because it is a sum of OI numbers, should also be an integer, and it is, though 4/4 = 1/1.
However, if we square (1/1), we get (1/1), but if we square (4/4), we get (16/16), and if we cube (4/4), we get (64/64), and even though 4/4 = 16/16 = 64/64 = 1/1, 4/4 units of motion squared is
(1/2 + 1/1 + 2/4)2 = (4/8 + 4/4 + 8/4) = 16/16 nm,
and
(1/2 + 1/1 + 2/4)3 = (16/32 + 16/16 + 32/16) = 64/64 nm
a completely different result.
There’s much more to say about OI numbers, but I’ll have to wait until next time to continue the discussion, including how we get the important results above.
Fourth Post in the BAUT RST Forum
The fourth post in the BAUT forum follows. These posts are a continuation of the RST thread in the “Against the Mainstream” forum of BAUT.
+++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
Larson proceeded to develop his scalar motion theory from the basic postulates of the RST, without the benefit of Hestenes’ work. Therefore, the concepts of duality and dimension, and how they are related to each other, as revealed in the binomial expansion, and the concepts of Clifford algebra that encapsulate these ideas in terms of n-dimensional numbers, though they were certainly available to informed specialists in the field of mathematics, during Larson’s time, they were scarcely visible to many uninformed specialists, let alone non-specialists. They didn’t become generally known until Hestenes’ efforts to use them as the basis for a new, unified, language of physics, began to gather steam in the eighties and nineties.
Today, we know that the purpose of GA, according to Hestenes, is to facilitate physics educational and research efforts. In delivering his 2002 Oersted Medal Lecture, “Reforming the Mathematical Language of Physics,” Hestenes told the audience:
| The generic name for that language is Geometric Algebra (GA). My purpose here is to explain how GA simplifies and clarifies the structure of physics, and thereby convince you of its immense implications for physics instruction at all grade levels. I expound it here in sufficient detail to be useful in instruction and research and to provide an entre to the published literature. |
- GA seamlessly integrates the properties of vectors and complex numbers to enable a completely coordinate-free treatment of 2D physics.
- GA articulates seamlessly with standard vector algebra to enable easy contact with standard literature and mathematical methods.
- GA Reduces “grad, div, curl and all that” to a single vector derivative that, among other things, combines the standard set of four Maxwell equations into a single equation and provides new methods to solve it.
- The GA formulation of spinors facilitates the treatment of rotations and rotational dynamics in both classical and quantum mechanics without coordinates or matrices.
- GA provides fresh insights into the geometric structure of quantum mechanics with implications for its physical interpretation. All of this generalizes smoothly to a completely coordinate-free language for spacetime physics and general relativity to be introduced in subsequent papers.
However, what few people knew, or could have even cared about at the time, was how the language that simplifies and clarifies the structure of vectorial physics, would also illuminate the work of Larson eventually. Indeed, its contribution to the science of scalar physics, may eventually prove to be more valuable to science in general than its contribution to the science of vector physics, since physicists and educators, well trained in the traditional language of vector and complex algebra, are relunctant to replace the known and familiar language of physics, with an unknown and unfamiliar one.
It may seem ironic that a new system of vector algebra, designed to improve the existing mathematical language of the mature science of vector physics, ends up providing a new mathematical language for the immature science of scalar physics. Yet, it is easy to understand it, when one looks at GA, not as a geometric algebra, but as a multi-dimensional number system that contains, as an integrated whole, advanced concepts of number that correspond to both scalar and vector magnitudes.
In starting our discussion of this expanded view of GA, it’s important to recognize that there is a pleasing, but mysterious, symmetry in the grouping of its n-dimensional basis numbers: 1 + 3 + 3 + 1 = 8, which seem to pair vectors and bivectors (3+3), and scalars and trivectors (1+1). When we interpret this mathematical symmetry geometrically, as the 2x2x2 cube, with the scalar basis point at the intersection of the three orthogonal basis vectors and the three orthogonal basis bivectors, a point which coincides with the center of the eight corners of the pseudoscalar basis trivector, the physical beauty in the symmetry of its form, the conceptual beauty in the symmetry of its algebra, and the intellectual beauty in its complete and flawless union of the meanings of direction, duality, and dimension, is simply startling in its power to make one marvel.
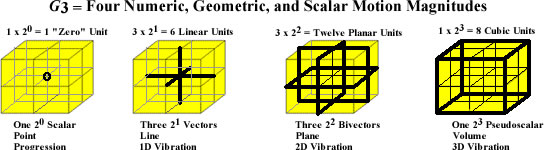
Figure 1. Larson’s Cube
I’ve dubbed it “Larson’s Cube,” because he initially used it to illustrate the eight units of three-dimensional scalar motion in the RST, but, now, when I look at it, it’s as if I see the physical, mathematical, and intellectual structure of the entire universe contained in its simple, three-dimensional, figure. It seems to me to contain the great secret of nature’s unity, as it were, the secret to how she unifies the continuum and the quantum, the secret that is the Holy Grail of theoretical physics.
Of course, I can’t prove these things yet, but I’m so convinced of their veracity that I have organized and incorporated the “Dewey B. Larson Memorial Research Center,” or “Larson Research Center,” for short, to employ the mathematicians, physicists, and other professionals who can perform the scientific work necessary to prove it, to the extent that it may be possible to do so.
The reason that I see so much beauty in this cube is that it seems to contain every element that is necessary for a theory of everything, but nothing more. It integrates the concepts of motion, mathematics, and geometry into one graphic, which can be viewed as a single expression of that motion, which in the RST, we assume is the one component of which the universe consists. To see it expressed in one graphic, is tantamount to looking at the very foundation of the universe, in all its awesome power.
Clearly, however, I’m getting ahead of myself. To understand the power of Larson’s Cube, we have to understand how it integrates the science of vectorial motion, with the science of scalar motion, and it all begins with the power of one, but not the quantitative interpretation of the number one, but the operational interpretation (OI) of the rational numbers as one.
As the ancient Greeks understood it, the number one (monad) represents eternity, and they probably learned it from the Egyptians, who in turn probably learned it from the Hebrews. In our OI number one, 1/1, we can understand this as signifying infinity/infinity is equal to 1/1; in other words, the number one contains all the numbers, 1/1, 2/2, 3/3, …n/n, where n goes to infinity.
Normally, this fact is regarded as trivial, until, that is, we realize that this unity, apeiron, to the ancient Greeks, is a principle of reality that subsumes (i.e. contains, encompasses) peiron, or that which is limited, bounded, finite. These are the notions of continuum and quantum, the very notions that are plaguing theoretical physics. Larson’s RST necessarily begins with this unity, which he calls the “unit progression” of space and time, as the initial condition of the universe of motion, because he defines space as the reciprocal of time, as motion, and motion as the sole component of the universe.
However, in describing the ancient Greek idea of this, we read in Wikipedia:
| When the apeiron is inhaled by the peiron it causes separation, which also apparently means that it “separates and distinguishes the successive terms in a series.” Instead of an undifferentiated whole we have a living whole of inter-connected parts separated by “void” between them. This inhalation of the apeiron is also what makes the world mathematical, not just possible to describe using math, but truly mathematical since it shows numbers and reality to be upheld by the same principle: both the continuum of numbers (that is yet a series of successive terms, separated by void) and the field of reality, the cosmos - both are a play of emptiness and form, apeiron and peiron. |
| …I decided to undertake the task of devising a method whereby the magnitudes of certain physical properties could be calculated from the chemical composition…As might be expected, the task that I had undertaken was a long and difficult one, but after about twenty years I had arrived at some interesting mathematical expressions in several areas, one of the most intriguing of which was an expression for the inter-atomic distance in the solid state in terms of three variables clearly related to the properties portrayed by the periodic table of the elements. But a mathematical expression, however accurate it may be, has only a limited value in itself. Before we can make full use of the relationship that it expresses, we must know something as to its meaning. So my next objective was to find out why the mathematics took this particular form. I studied these expressions from all angles, analyzing the different terms, and investigating all of the hypotheses as to their origin that I could think of. This was a rather discouraging phase of the project, as for a long time I seemed to be merely spinning my wheels and getting nowhere. On several occasions I decided to abandon the entire project, but in each case, after several months of inactivity I thought of some other possibility that seemed worth investigating, and I returned to the task. Eventually it occurred to me that, when expressed in one particular form, the mathematical relation that I had formulated for the inter-atomic distance would have a simple and logical explanation if I merely assumed that there is a general reciprocal relation between space and time. |
| My first reaction to this thought was the same as that of a great many others. The idea of the reciprocal of space, I said to myself, is absurd. One might as well talk of the reciprocal of a pail of water, or the reciprocal of a fencepost. But on further consideration I could see that the idea is not so absurd after all. The only relation between space and time of which we have any actual knowledge is motion, and in motion space and time do have a reciprocal relation. If one airplane travels twice as fast as another, it makes no difference whether we say that it travels twice as far in the same time, or that it travels the same distance in half the time. This is not necessarily a general reciprocal relation, but the fact that it is a reciprocal relation gives the idea of a general relation a considerable degree of plausibility. |
| So I took the next step, and started considering what the consequences of a reciprocal relation of this nature might be. Much to my surprise, it was immediately obvious that such a relation leads directly to simple and logical answers to no less than a half dozen problems of long standing in widely separated physical fields. |
According to the Wikipedia article, this same challence faced the ancients:
| What really sets this apart from Anaximander’s original ideas is that this play of apeiron and peiron must take place according to harmonia (harmony), about which Stobaeus commentated: “About nature and harmony this is the position. The being of the objects, being eternal, and nature itself admit of divine, not human, knowledge – except that it was not possible for any of the things that exist and are known by us to have come into being, without there existing the being of those things from which the universe was composed, the limited and the unlimited. And since these principles existed being neither alike nor of the same kind, it would have been impossible for them to be ordered into a universe if harmony had not supervened – in whatever manner this came into being. Things that were alike and of the same kind had no need of harmony, but those that were unlike and not of the same kind and of unequal order – it was necessary for such things to have been locked together by harmony, if they are to be held together in an ordered universe.” A musical scale presupposes an unlimited continuum of pitches, which must be limited in some way in order for a scale to arise. The crucial point is that not just any set of limiters will do. We cannot just pick pitches at random along the continuum and produce a scale that will be musically pleasing…In Philolaus’ terms the fitting together of limiters and unlimiteds involves their combination in accordance with ratios of numbers (harmony). Similarly the cosmos and the individual things in the cosmos do not arise by a chance combination of limiters and unlimiteds; the limiters and unlimiteds must be fitted together in a “pleasing” (harmonic) way in accordance with number for an order to arise. |
| The question that naturally arises at this point is, How can these displacements of the space-time ratio exist, when each unit of space is always equivalent to a unit of time? Inasmuch as the progression is scalar, the only variation that can take place is in the scalar direction: outward (positive) or inward (negative) …But…one of the components may alternate scalar directions, so that the negative progression of one unit of this component cancels the positive progression of the preceding unit. A series of such reversals thus results in the formation of a multiple unit of motion in which n units of space (or time) are associated with only one unit of time (or space). |