The New Mathematics
LRC Seminar (cont)
In the previous post, I discussed the combination of 1/2 and 2/1 as combining two, equal, numbers with opposite “directions.” Since, in ordinary arithmetic, the sum of these two numbers is taken as the sum of a fraction and a whole number that can’t be equal to one another, by definition, this seems strange.
However, as soon as it’s understood that the interpretation of the reciprocal numbers is not a quantitative interpretation, but an operational interpretation, and that there are two operations that can be found, things begin to clear up. The first operational interpretation is the ordinary interpretation of division of whole numbers. Thus, under this interpretation, 1/2 = .5 and 2/1 = 2, but, under the second interpretation, 1/2 = -1 and 2/1 = +1, which shows us that, under the first interpretation of division, 2/1 = 2 is actually +.5, the inverse of 1/2 = -.5, when we take reciprocal “directions” into account.
Of course, it’s true that we can’t ignore the difference that the “direction” of a reciprocal number makes in the relative value, because 2 (+.5 in disguise, we might say) is four times greater than -.5. For example, if we divide +.5 by -.5 on a calculator, we get
.5/-.5 = -1,
not 4. Hence, we have to recognize that +.5 is the operational interpretation of 2/1, but that
1/2 * 2/1 = 2/2 = 1/1 = 1,
just as
.5 * 2 = 1.
In other words, In using reciprocal numbers, it’s best not to interpret the value of the reciprocal relation, until the arithmetic is completed, in order to avoid error and confusion. Indeed, to help eliminate confusion, as much as possible, we use a different symbol, the pipe symbol, to indicate the reciprocity of the number, when it is to be interpreted under addition,
1|2 + 2|1 = 3|3 = 1|1 = 0 (i.e. -1 + 1 = 0).
When the reciprocal relation is to be interpreted under multiplication, we use the customary symbol, the slash symbol, to indicate the reciprocity of the number,
1/2 * 2/1 = 2/2 = 1/1 = 1 (i.e. .5 * 2 = 1).
It has been suggested that we need a different symbol for the sum operation to avoid the confusion with ordinary arithmetic, where
1/2 + 2/1 = .5 + 2 = 2.5
and
-1 * 1 = -1.
However, it’s clear that this is not necessary, if we understand that the addition operation is always used with the reciprocity indicated by the pipe symbol, and multiplication operation is always used with the reciprocity indicated by the slash symbol. In both cases, as long as numerators are combined with numerators, and denominators with denominators, under the appropriate binary operation for the indicated reciprocity, no confusion results.
What about combined operations? For example, what is the meaning of
(1|2)/(2|1) = -1/1 = -1, or (1/2)|(2/1) = (-.5)|(2) = -1.5?
This is problematic, because “direction” is only defined in the reciprocal relation of whole numbers, not in the numbers themselves. Since the numerators and denominators are inverses of each other, the operations should yield the appropriate identities of the respective groups (i.e. 1 and 0). However, if we do what we have always done in the ordinary arithmetic of fractions, invert and multiply the denominator, we get, for the slash reciprocity,
(1|2)/(2|1) = (1|2) * (1|2) = (-1) * (-1) = 1.
If we do the same thing for the piped reciprocity; that is, if we invert the denominator and the operation, which means we invert and add, instead of subtract, we have to recognize that the inversion doesn’t change the “direction” of the denominator,
(1/2)|(2/1) = (1/2) + (1/2) = (-.5) + (+.5) = 0,
which yields the respective identities in each case, as required.
I won’t be able to go into this level of detail in the presentation, certainly, but if the question comes up, I’ll be prepared with the answer: The “directions” of numbers are conserved in the sum and multiplication (subtraction and division) operations of reciprocal numbers. Once that is established, I will proceed to show how we find the third property of numbers, multiple dimensions, clarifying the difference between the powers of a number, as multiple factors, and the dimensions of a number, as independent sets of reciprocal, or dual, “directions.”
That will be in the next post for sure this time.
LRC Seminar
An LRC seminar is scheduled for next month in which I am to present the new concepts of the reciprocal system of mathematics (RSM) to a group of professional mathematicians, physicists, and engineers. Some are familiar with Larson’s reciprocal system of physical theory (RST), but others are not. Needless to say, the challenge seems formidable at this point.
I’m planning on placing the discussion in the context of empirical discoveries as much as possible, starting with the discovery of the Pythagorean incommensurables. I’ll talk about the historical effort from that point on to generalize the concept of number enough to identify its properties with the properties of physical magnitudes in the attempt to found a geometric algebra. I’ll point out the often overlooked, or misunderstood, significance of the mathematical implications of Newton’s third law of motion, which leads to the corollary that for every direction there is an opposite direction, or, which is tantamount to the same thing, that each dimension of space has reciprocal, or dual, directions.
Then I’ll want to show that Hamilton discovered that, for the science of algebra, as opposed to the science of geometry, considering the mathematical inequalities in the order in progression makes more sense than considering them in terms of increasing and diminishing magnitudes, but that this has gone unrecognized in the world opened up by Dedekind and Cantor.
I probably won’t be able to sufficiently, and succinctly, capture the compelling drama between the misdirected development of mathematical ideas, lamented by Hamilton, and the success of their physical applications, which obscures their imperfections, without confusing the audience. So, instead, I’ll just try to show that what Hamilton discovered, when combined with what Larson discovered, sheds light on what Hestenes revealed lies hidden in the Clifford algebra, based on the Grassmann algebra, when combined with Hamilton’s ideas: namely, that the generalization of number in terms of the definition of geometric algebra’s (GA) geometric product enables us to work with coordinate-free vectors in 3D space, under a new interpretation of imaginaries, interpreted as rotations, defined in terms of GA multivectors, arising out of the four vector spaces of the three-dimensional line of the tetraktys (1331), enabling the formation of an eight dimensional algebra, corresponding to the three-dimensional geometry of the tetraktys.
However, I will make the point that GA does not eliminate the idea of imaginaries in its formulation. It merely transforms this enigmatic, ad hoc, invention of the human mind, which was invented to deal with negative numbers, from the quantitative interpretation of the square root of -1, to the operational interpretation of a π/2 rotation, by introducing two products, one the dual, or the reciprocal, of the other.
Then, I hope to make clear that this idea of a π/2 rotation originated in the four dimensional quaternions, coming to Clifford from Hamilton, and thus on to Hestenes and the eight-dimensional GA of today. The great significance of this fact is that GA is founded on a mistaken notion that not only caused a hundred years of great confusion (before Hestenes’ work and the advent of GA), which is aptly described by Simon Altmann, but incredibly enough, goes on to connect the RSM to the tetraktys and its geometry found in Larson’s cube, the foundation of the RSM, and the basis for the RST-based theoretical development at the LRC.
To show what I mean, I will begin with a one-dimensional magnitude, a line segment, and treat its properties logically. To wit: If we divide it into two equal lengths, each length will be .5 times the original 1 unit, but the half-lengths have opposing direction with respect to the center cut of the original. Yet, combining them arithmetically, as usual, we generally ignore this difference in the direction to get
.5 + .5 = 1,
because, if we include the opposite direction information, we get
-.5 + .5 = 0,
which, in terms of physical length, makes no sense, because combining the two half-lengths should give us the original unit length again, not nothing, a point. Of course, if we put opposing arrow heads on the two lengths, representing two magnitudes with two opposing directions, the result of combining them is 0, as in the resultant zero motion of two opposing force vectors.
However, when Larson recognized the two “directions” of speed-displacement that the two reciprocal, space|time, progressions can take, we were able to see that the same two numbers can take a different form
-.5 + .5 = 1/2 + 2/1 = -1 + 1 = 1,
even though it makes no sense in the context of usual arithmetic, which we would normally understand as tantamount to writing
0 = 2.5 = 0 = 1.
Even so, this complete nonsense, in terms of grade school arithmetic, makes perfect sense in terms of recombining two half-lengths, if we understand that -.5 = 1/2 and .5 = 2/1, in terms of a unit displacement in two, opposite, directions, as when two girls are on one side of a teeter-totter opposite one boy, or vice versa. The displacement is one unit in one direction, or the the other: One is in a vertical position that is a positive unit, while the other is in a vertical position of equal magnitude that is a negative unit relative to the equilibrium condition. If we place two boy and girl teeter-totter triplets, one with two boys and the other with two girls, onto one teeter-totter, we will have three kids on each side of the teeter-totter, and, if they all weigh the same, it will be balanced. So, the arithmetic
1/2 + 2/1 = 3/3 = 1/1 = 1
is ordinary arithmetic after all, when we interpret the numbers as reciprocal numbers, with opposing directions.
The teeter-totter analogy is very useful in this respect. For instance, if we have, say, two boys standing in the middle of the device, they could walk in opposite directions, and, if they were careful enough, they could keep the beam balanced until they reached the ends and took their seats. As far as the condition of equilibrium is concerned, though, no change has taken place, although now there is a distance between them, which didn’t exist before. Clearly, this is analogous to the equation
1/1 = -1 + 1 = 1,
if we interpret the numbers in such a way that the positive and negative values offset one another, but do not annihilate each other. In this interpretation, the numerator and denominator of reciprocal numbers are interpreted as having opposing “directions,” where placing quotations around the word directions indicate that we mean the dual directions of polarity, not the dual directions of space.
Therefore, we can clearly establish that the reciprocal number has both quantity and the dual direction of dimension. After establishing this important concept in the presentation, I will try to show that these reciprocal numbers also have the third property of physical magnitudes, the property of three dimensions. Once that is established, I will want to go on to show how these numbers, with their three properties of physical magnitudes, quantity, dimension, and “direction,” define an eight-dimensional scalar algebra, that is remarkably similar to the eight-dimensional vector algebra, GA.
More on that next.
Developing SA
Just the thought of developing a 3D scalar algebra (SA) is enough to make me want to run home, climb in bed, and assume a fetal position. I am so intimidated by this prospect, yet I have to face the challenge no matter how daunting, if we are to have any hope of making significant progress toward our goal of calculating the atomic spectra, and the properties of matter, using RST-based theory.
The truth is that scalar motion is not vector motion, and the difference makes a 3D scalar algebra (and a scalar calculus) necessary. However, just as the scalar magnitudes are not unrelated to vector magnitudes, scalar algebra (and calculus) are not unrelated to vector algebra (and calculus.)
Our approach is based on using geometric algebra (GA) as a guide in the development of SA, because we have found the relation between the reciprocal numbers of the RSM, and the binomial expansion - based Clifford algebras that the 3D GA is built on, through the tetraktys. Nevertheless, the difference between the 1D vector motion in 3D space that GA describes, and the multidimensional scalar motion in 3D space|time that the SA must describe, makes it imperative that the development of SA is based on logical deduction from first principles; that is, we must ensure that its principles follow as necessary consequences from the fundamental postulate that we have assumed: that all mathematics stems from order in two, reciprocal, progressions. This is an extension of Hamilton’s premise, as expanded by Larson.
As explained in previous posts below, the discovery that two groups are defined from one set of reciprocal numbers (RNs) by the operational interpretation of number, wherein the difference operation between the numerator and denominator of the RN forms a group under addition, while the division operation forms a group under multiplication, enables us to achieve a level of unprecedented mathematical integration, even though all the ramifications of that fact are not all understood yet.
What we are trying to do now is apply the RN to the tetraktys, so that we can use the analogy of vector geometry, that is the points, lines, areas, and volumes of Euclidean geometry, to shed light on scalar “geometry.” Clearly, the idea of scalar geometry seems absurd, until we realize that the “direction” of scalar poles is analogous to the direction of vector distance, and the independence of scalar combinations is analogous to the orthogonality of vector dimensions.
However, once this much is understood, we can proceed to analyze the way GA applies to vector geometry and vector physics, and use that knowledge to illuminate our path to understanding how SA would apply to scalar “geometry” and scalar physics. In the previous posts below, we saw that (n/n)0 represents a given number of steps of reciprocal progression, and that, with one step (1/1)0, we have no degrees of freedom in our inherent duality, the two opposing scalar “directions.” This, then, is analogous to the point in vector space, our initial number in the tetraktys, representing a single system of numbers (in the legacy system of mathematics (LSM), this is the class of real (1D) numbers.)
But with two steps of progression (2/2)0, we have one degree of freedom, giving us an expanded system of numbers, with two classes of numbers analogous to points and lines in vector space (in the LSM, this is the system of complexes (i.e. 2D numbers.)) With four steps of progression (4/4)0, we have two degrees of freedom, expanding the number system further to include a third class of numbers, analogous to areas in vector space (in the LSM, this is the system of quaternions (i.e. 4D numbers.)) With eight steps of progression (8/8)0, we have three degrees of freedom, giving us the fully expanded system of numbers, with a total of four classes of numbers, analogous to points, lines, areas, and volumes in vector space (in the LSM, this is the system of octonions (i.e. 8D numbers.))
Of course, the LSM number system uses the invented concept of the “imaginary” number to accommodate the inherent duality of directions in vector geometry, which GA reinterprets in a specific and well-defined way, eliminating in the process much of the complexity that this ad hoc invention introduces into mathematics. It turns out, however, that the approach used in GA to do this is also based on a non-intuitive, ad hoc, invention called the geometric product, and thus this advance actually complicates our efforts to apply the concepts of GA to the development of SA, in a straightforward manner.
Nevertheless, we’ve made some progress, by taking advantage of the fact that Larson’s cube encodes the geometry of the tetraktys, which enables us to distinguish the difference between the geometry of duality in GA, and the geometry of the inherent, 3D, duality that SA must incorporate. We can clearly see that the difference stems from the contrast of vector and scalar motion. Vector motion is 1D motion in 3D space, while scalar motion is 3D motion (with 1D and 2D components.)
With the knowledge of this difference, we were able to discovery the degeneracy of the three dimensions in vector space, wherein one dimension must always be redundant, and thus hidden, in the three, orthogonal, axes of Larson’s cube. This is apparent, because, as we double the inherent duality of scalar space, in the tetraktys, the (8/8)0 point of the cube consists of the intersection of four (2/2)1 “lines.” These are the four diagonals of Larson’s cube indicating the eight directions of 3D vector space, as well as the eight “directions” of scalar space.
The degeneracy is not important to GA, since the 3D volume (pseudoscalar) space of the tetraktys is the container of 1D vector motion. Of course, this is not the case for scalar motion, where the pseudoscalar is the inverse of the scalar, and constitutes the highest form of the motion itself. For this reason, we have to choose a different basis set of unit “directions” for SA, which immediately confronts us with the challenge of redefining multiplication in SA, bringing us to the consideration of the almost imponderable geometric product of GA.
Our new basis set is
e0, the (8/8)0 scalar at the intersection of the 2x2x2 stack of unit cubes:
(2/2)0 + (2/2)0 + (2/2)0 + (2/2)0 = 8/80, and
e1, e2, e3, e4,
the positive unit “directions” formed by the four 2/1 halves of the eight diagonals, each with their inverses, the four negative unit “directions” formed by the four, reciprocal, halves of the eight diagonals (1/2).
This is a big change, because not only is the number of elements in the 1D basis set one more in the SA set, than in the GA set, but the inverses (negatives) of each of these is an independent negative unit, on the other side of the intersection (unity) of the four diagonals. In contrast, the three unit vectors used as the basis set in GA, if I understand correctly, have their inverses construed as the reverse direction of the same unit; that is, the three positive directions diverge from the point, while the three negative directions converge to the point.
Thus, in effect, the geometry of GA is derived from one of the eight unit cubes in the 2x2x2 stack, called the dextral basis set, or right-handed set, of unit vectors. This is huge in our effort to understand how to “map” the GA algebra to the SA algebra. We know that we have four basis scalars, as we might call them, but they are 1D scalars, analogous to the four diagonals in the four unit cubes on one side of the 2x2x2 stack of unit cubes, diagonally opposite the four diagonals in the four unit cubes on the other side of the stack. Thus, we have to have, in effect, a different basis set for each of the eight 3D cubes in the stack. It’s hardly worth calling them basis sets, because there is no basis common to them all.
When we think about it this way, we see that the dextral basis set in GA is used to describe points, vectors, and bivectors, in one cube, or in one 3D volume, of the eight 3D volumes that are available in the 2x2x2 stack, the geometric version of the tetraktys. In the RST-based theory, we have no need for a mathematical language, such as GA, to describe points, or the locations of points, or the orientations, directions and magnitudes of lengths between points, or the orientations and magnitudes of planes between lengths, in the dextral cube, of the stack. Instead, we need a mathematical language to describe the distribution of scalar magnitudes within the 2x2x2 stack, as a whole, within a fixed scale, although there still is an infinite set of possible scalar combinations in the stack, just as there is an infinite set of possible vector combinations in the dextral cube, with a variable scale.
That is to say, the basis values in GA, inside the dextral cube, represent the scale of lengths, which are then taken as the value of the scalar, or multiplier, α, used to multiply, or divide, individual vectors and bivectors in the algebra, while the basis value in SA, that which sets the scale of the system, must be the scalar itself! Thus, in SA, if we start with the minimum point (1/1)0, the scale of the system is set to the scale of a single point; If we double the scalar to (2/2)0, the scale of the system is expanded up to the scale of lines; If we double the scalar again to (4/4)0, the scale of the system is expanded up to the scale of planes; Finally, if we double the scalar once more, to (8/8)0, the scale of the system is fully expanded to include points, lines, planes, and volumes.
Of course, we can double again, and again, ad infinitum, in principle, but, as we do, we increase the density of points, lines, planes, and volumes, so to speak. It’s why Bott’s periodicity theorem limits us to period eight. We complete a 3D system with every factor of eight scalar expansions, as the scalar continues to double. However, we are getting ahead of ourselves. We need to fully understand the first tetraktys at this point. Later on, we double it in the second tetraktys.
In the first T, we have eight 3D cubes that make up one 2x2x2 stack. We know that the scalar, at the intersection of the stack, has the value (8/8)0, made up of the four diagonals, the four (2/2)0 values it takes to create four independent 1D numbers, each containing 1/2 and 2/1 “directions,” or one degree of freedom. Now we can see that taking four of these eight cubes on the same side of the scalar (intersection at the center of the cube) defines a plane of cubes, with an inverse plane on the other side of the intersection point (scale-setting scalar), and that there are exactly three ways to select a plane of four cubes in the stack, corresponding to the three, orthogonal, faces of the planes in the stack.
Interestingly enough, this gets us back to the 23 = 8 total dimensions of the four linear spaces, giving us the binomial expansion of the fourth line of the tetraktys, associated with Larson’s cube; that is, the total numbers of these spaces is 1421 = 8, which is isomorphic to the standard 1331 = 8 (I guess we lose our connection with string theory’s 10 dimensions, though. Oh well!).
Clearly however, if this is the way to go from 1D to 2D geometrically, then we need to find an algebraic operation that will raise and lower the dimensions of these numbers. Yet, this seems problematic from the outset, because the 2D plane is made up of four 3D cubes! To do this we have to consider the four 1D lines, as 3D points, or 3D “directions,” not 1D “directions.”
Of course, that was exactly Larson’s point: The four diagonals are the four dual, or eight, 3D, “directions,” of scalar magnitudes. This may give us a clue as to the needed operations of SA: Instead of multiplying, we divide, and instead of thinking of building up from the 0D scalar (actually 1D vector) to the 3D pseudoscalar (volume), we think of decomposing, from the 3D pseudoscalar to the 0D scalar (actually 1D line). On this basis, the plane is a two-part division of the 2x2x2 stack of unit cubes, the line is a two-part division of the plane of cubes, and the point is a two-part division of the line. Notice that the “direction” of each division operation is orthogonal, or independent, of the others: The line division “cut” is orthogonal to the plane division “cut,” while the point division “cut” is orthogonal to both.
This bodes well for the prospect of defining a scalar algebra for the scalar tetraktys.
Analyzing SA's Ten Dimensions
In the previous entry below, we found that the four linear spaces of our new scalar algebra (SA) do not have the same number of dimensions as the four vector spaces of geometric algebra (GA), the 1+3+3+1 = 8 dimensions of dual directions, using the word dimension in the mathematical sense of independent variables. Instead, they contain 1+4+4+1 = 10 dimensions. The same number of space dimensions in string theory (m-theory).
Yet, that these 10 mathematical dimensions are contained in the 3D geometric space of the tetraktys is now clear, when we see them as the 2x2x2 stack of cubes, which Larson used to describe the 3D units of scalar motion. String theorists, unaware of the concept of scalar motion, have tried for many decades to employ these dimensions in terms of the usual concepts of vectorial motion, without success, leading to confusion of thought and perplexing complications in their topological approaches (see the Calabi-Yau manifold), with serious theoretical, philosophical, and even sociological ramifications (see our Trouble With Physics blog).
However, if we compare the four linear spaces of GA, with the analogous spaces of SA, in terms of the geometric properties of Larson’s cube, we get a view of the scalar spaces in terms of linear, circular, and spherical expansions and contractions, as discussed last time. Nevertheless, it’s not clear yet what we gain by this transformation, and we are still investigating it. In the meantime, though, it’s not difficult to see that the four “lines” of the 1D scalar space can be used algebraically to generate four groups of 2D scalar space, and that these groups have exactly 12 2D entities, which correspond to the 12 2D panels in the three intersecting, orthogonal, planes of the stack.
That these 12 2D scalar values correspond to the 12 2D areas of the vector space is also very intuitive, but, the comparison of them has revealed something odd about GA, which is not very intuitive. To explain this, we need to analyze the geometry of the 2x2x2 stack of unit cubes. Using the four diagonal lines of the stack to generate the 12 2D “areas,” we can describe them as the 2D products of the four sets shown in the graphic below.
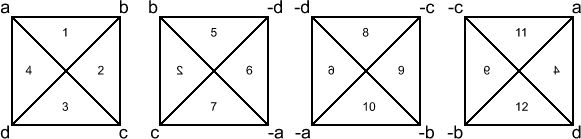
Figure 1. Four Sets of 2D Scalar Products
As can be seen above, we first denote one end of each diagonal in the stack, as a, b, c, and d, starting with the upper left corner of one face of the 2x2x2 stack, as indicated, in the left-most face in the graphic. The inverse of each 1D diagonal (reflection symmetry in 1D space), is the opposite end of the diagonal, in the diagonally opposing, 3D, unit cube (recall there are eight of these). Thus, the unit cube containing -a is diagonally opposite the unit cube containing a, while -b is diagonally opposite b, and so on.
Next, we designate each 2D area, the product of two 1D diagonals, with numbers, beginning with 1 and continuing clockwise. On this basis, the first face contains four 2D products, but the point where the diagonals cross is in the center of the cube, so the face is indented at the center. Hence, the face of the stack of cubes is actually the projection of the diagonal lines onto the stack face, while the lines themselves only contact the face at the corners a, b, c, and d, forming a four-sided pyramid in the interior of the stack, with the apex at the center of the stack, and each numbered facet constituting a congruent isosceles triangle.
Rotating the stack clockwise, as viewed from the top, to view the next face, shown on the right of the first in the graphic, illustrates the second set of pyramid forming triangles, with the four points at the base of the interior pryamid (projecting the next face of the stack) now rotated into the plane of the page, and its apex coinciding with the apex of the first pyramid, at the point of intersection, at the center of the stack.
Notice that there are only three unique, numbered, facets in this set, since one facet is common to the first set (facet number 2, of the first face, now rotated into the page). A second rotation brings up the third set, which, again, has a common (thus not counted) facet, with the preceding set. Finally, the fourth set has only two unique triangles, in the pyramid, since it has common facets with both the beginning set and the preceding set of facets.
It’s interesting to note that the degeneracy of the three axes, in the vector spaces (see discussion below), which we have removed by switching to the four diagonals of the 2x2x2 stack, seems to reappear in the redundant form of the four common facets. However, there seems to be something else, even more significant, revealed by the switch to these scalar spaces (recall that the directions inherent in the stack of 8 unit cubes are actually scalar “directions” in this view.) This revelation is the fact that we would expect that the algebraic properties of these scalar spaces are ordered, commutative, and associative, since they are scalar spaces with “direction,” not vector spaces with direction.
In GA, a 1331 basis is selected, where e1, e2, and e3 are regarded as the three 1D unit vector directions. In this way, the e1^e2, e1^e3, and e2^e3 bivectors define three 2D unit outer products (we’ll ignore the inner and geometric products for now), and any of these wedged with the odd man out, (e1^e2)^e3, (e1^e3)^e2, (e2^e3)^e1, define one of three, 3D, trivectors. In other words, the pseudoscalar can be defined in three, equivalent, outer products.
Notice, however, that the scalar is not derived, and neither are the three basis vectors, but, as we have seen, they represent the assumed 0D point space and the three, orthogonal, dimensions of geometry, from which all else is derived. The scalar is designated α, and it is used to multiply the unit vectors in the algebra. All these spaces taken together, form a multivector, which has proven very useful for doing physical calculations.
However, in the scalar spaces of the SA, everything is defined, beginning with the 0D scalar and then proceeding to the 3D pseudoscalar. In this algebra, the scalar is defined and the basis is actually derived, because it grows, as the scalar grows. Thus, at zero dimensions, (1/1)0 and (8/8)0 are both a point, and there is no distinction, but at three dimensions, (8/8)0 and (2/2)3 form an assembly of a point expanded in three “directions,” defining eight, one-unit, cubes, in the 2x2x2 stack. So, we can say that (8/8)0 really is the potential of (2/2)3; that is, one is transformable into the other, both numerically and physically.
So, what can we take as a basis for these multi-dimensional scalar units in SA? The logical answer is the four, two-unit, scalar, “distances,” (a to -a), (b to -b), (c to -c), and (d to -d) above. This would give us the bases for the 10 dimensions of the 1441 scalar tetraktys:
e0; e1, e2, e3, e4; e1^e2, e2^e3, e3^e4, e4^e1; (e1^e2)^e3(^e4); (e2^e3)^e1(^e4); (e3^e4)^e1(^e2); (e4^e1)^e2(^e3);
where the parentheses around the fourth dimension indicate that the basis of the 3D scalar can be formed in one of two, equivalent, ways, as a product of each 2D scalar, with either of the two remaining 1D diagonals, forming the 3D scalar (pseudoscalar). Now, the interesting thing about this is, following GA, each n-dimensional scalar should have its inverse. For instance, the 1D scalars|inverse scalars would be:
e1|-e1; e2|-e2; e3|-e3; e4|-e4;
but where the negative sign does not indicates the opposite direction of a vector, but the opposite “direction” of a scalar; that is, positive and negative in a real sense. In other words, using reciprocal numbers, we get four pairs of (1/2)|(2/1), that are equivalent to the four diagonals.
e1|-e1 = (1/2):(2/1)|(2/1):(1/2),
e2|-e2 = (1/2):(2/1)|(2/1):(1/2),
e3|-e3 = (1/2):(2/1)|(2/1):(1/2),
e4|-e4 = (1/2):(2/1)|(2/1):(1/2),
where the colon symbol is used to indicate the “difference” between the positive and negative reciprocal numbers (RNs), and the pipe symbol is used to separate the “directions” of the positive and negative bases. Therefore, we see that the eight scalar “directions” are perfectly analogous to the eight vector directions, relative to the center intersection of the four diagonals, in the 2x2x2 stack.
However, this is where the odd aspect of GA begins to show up. No one would suggest that this set of four diagonal directions would be taken as a basis set in vector algebra, because they are not independent, or orthogonal. Yet, as we see in figure 1 above, the projection of them onto the respective faces is orthogonal. In fact, the change in the location of the intersection, from the center of the face to the center of the stack, at the apexes of the four pyramids, constitutes a change in an independent direction and therefore does not affect the magnitude in the two, orthogonal, dimensions. Thus, there is no inherent reason why we couldn’t use the set of four diagonals as a basis set, but only a practical reason not to: It simply complicates matters from a vector point of view, and with no motivation for doing it, it has never been done, at least as far as I know.
Indeed, in GA, if I understand correctly, the basis set, the dextral, or right-handed, set, taken as the basis set, is not the set of vectors defined at the interior intersection of the stack, as I have always assumed, but it is the set of vectors defined from one of the exterior corners of the stack! Thus, the negative basis represents a reversal of the outward direction, a reversal of the outward direction from one corner, to the inward direction toward the corner. In other words, in GA, the geometric interpretation of the positive basis set diverges from the dextral corner, while the negative basis set converges to the dextral corner.
Therefore, the difference between the basis set of three directions in GA, and the basis set of the four diagonals we are contemplating using for SA, is a divergence|convergence of the three directions at the corner, as opposed to the divergence|convergence of the four directions at the intersection.
This difference has many implications that we need to explore.
Pressing On
We have started discussing the construction of a scalar algebra (SA), using Hestenes’ geometric algebra (GA), as a guide. However, whereas GA is formulated axiomatically, beginning with an abstraction of natural numbers from the traditional set theory of Dedekind and Cantor and continuing with a further abstraction regarding algebraic operations from Clifford and Hestenes, SA must be deduced from the purely inductive principles of order in progression.
This is a tall order, to say the least. First, Clifford and then Hestenes recognized Grassmann’s geometric product and Hamilton’s quaternions, as containing the seeds of an eight-dimensional, geometric, algebra. Nevertheless, few seem to share Hamilton’s concern with the axiomatic foundations of formalizations such as GA that disregard the fact that many times one cannot “rise to intuition from induction, or cannot look beyond the signs to the things signified” in these formalisms.
Hestenes tauts GA as a very useful language for physics, and has impressively demonstrated its power in that connection, but it seems that Hamilton would object on theoretical grounds, because, he would certainly protest that, while there is much of beauty and consistency “in what has already been brought to light,” there is still considerable confusion of thought in what the foundations of this algebra are. He writes in the preface to his essay on the Algebra of Pure Time:
The thing aimed at, is to improve the Science, not the Art nor the Language of Algebra. The imperfections sought to be removed, are confusions of thought, and obscurities or errors of reasoning; not difficulties of application of an instrument, nor failures of symmetry in expression. And that confusions of thought, and errors of reasoning, still darken the beginnings of Algebra, is the earnest and just complaint of sober and thoughtful men, who in a spirit of love and honour have studied Algebraic Science, admiring, extending, and applying what has been already brought to light, and feeling all the beauty and consistence of many a remote deduction, from principles which yet remain obscure, and doubtful.
As we have already noted extensively, Hamilton’s approach was based on turning from considering the “bounded notion of magnitude,” to what he called the intuition of order in progression, the principles of which he deduced from inductively reasoning upon “pure time.” However, this approach seemed complicated and unnecessary to formalists who were seeking to improve the “art of language,” and the fact that the accepted concepts of negatives and imaginaries work well in practice is apparently good enough for them. That a theorist like Hamilton, seeking to improve the science of algebra, might be bothered by “principles which yet remain obscure and doubtful,” seems hardly enough to turn the thoughts of mathematicians, let alone physicists, to the intuition of pure time.
Yet, we have seen that, with the ideas of Larson, beginning a century later, the concept of numbers and magnitudes, deduced from the properties of order, in assuming a space|time, reciprocal, progression, leads to a generalization of number that is remarkably consistent with the three properties of physical magnitudes, their quantity, dimension, and direction properties. Now, when we look at Clifford algebras, we can see that the idea of dimension is associated with the idea of direction; that is, as dimension increases, the two directions of the dimensions increase, as seen in the binomial expansion. Thus, in the tetraktys, the two, inherent, directions of dimension multiply from zero, to two, to four, and to eight, in its four levels, creating a corresponding algebra of directions, we might say, with each successive one including the previous ones.
Therefore, in the third dimension, fourth counting zero, we have a Clifford algebra containing four linear spaces of dimension 0 through 3, describing what mathematicians call an eight-dimensional algebra that should be useful for calculating geometrical magnitudes, except that, because of the obscure and doubtful principles of negatives and imaginaries, the 1D space is not ordered, the 2D space is not commutative, and the 3D space is not associative, and without these crucial algebraic properties, the operations of multiplication in the algebra break down.
What Hestenes revealed, in the last half of the 20th Century, is that these problems can be overcome with Clifford’s formulation of the geometric product, if it is used to define the inner and outer products of vectors, which can then be interpreted as the magnitude and direction components of vector products in 3D space. While this is a truly amazing development in the art of mathematics as a language for physics (it is finally beginning to be recognized and taken seriously by the scientific community, mostly because engineers have found it so useful), it would hardly have been satisfying to Hamilton. The principles involve yet remain obscure and doubtful. It seems like intellectual acrobatics, rather than clean theoretical deduction, useful, but unable to reveal the foundations of truth in the structure of the physical universe.
In some sense, our own feeble attempt has the same object as Hamilton’s initial efforts had; that is, “to improve the science of algebra,” even though there is an ulterior, less noble, motive behind our efforts, because we simply need a scalar algebra to develop RST-based physical theory, due to the fact that a vector algebra does not apply to scalar magnitudes. Our first step was to deduce a set of natural, reciprocal, numbers, in a set theoretical manner (see previous posts below). Next, we plugged these numbers into the tetraktys, which gave us the same four linear spaces, used in the eight-dimensional GA. However, we know that the geometric product of GA, and consequently, the derivation of the inner and outer products, cannot be directly applicable to a SA, because there are no vectors, bivectors, or trivectors in our four linear spaces.
In fact, there is something very disturbing about the four linear spaces of the scalar tetraktys. While (8/8)0 is composed of four (2/2) 1D units, our 1D linear space, like the linear space of the vector tetraktys, has room for only three of these! What are we supposed to do with the fourth set? In thinking why this has happened, it soon becomes clear that there is a degeneracy in the vector tetraktys, because of the way it is applied to Larson’s cube, in terms of vectors, bivectors, and trivectors. To see this, we need to think of 23 = 8, as generated from two instances of 22 = 4, or the 3D space, as generated by a rotation of two dimensions out of the plane. There are two ways to do this: Rotate the second plane around the horizontal axis of the first, or else rotate it around the vertical axis of the first.
Either way, a 3D space is generated from a 2D space, by the rotation. However, in both cases, the axis of rotation is common to both planes! They are tantamount to what Hestenes would designate as colinear vectors. Applying this to the scalar spaces, it’s as if the colinear axis were composed of the “distance” (2/4, 4/2), instead of the “distance” (1/2, 2/1), so one entire 2/2 unit is hidden, as a degeneracy.
The significance of this may take a while to fully appreciate, but in the meantime we can recognize that it will not do. We must deal with it, because rotation is not possible with scalars. Either the degeneracy does not exist in our scalar spaces, in which case the dimension will change, or there is another mechanism that produces the same degeneracy in the scalar tetraktys. Biting the bullet, we are going to assume, at least for now, that we have to put the fourth unit back in, which would change the scalar tetraktys to:
1
1 1
1 2 1
1 4 4 1
or from an eight-dimensional algebra, to a ten-dimensional algebra (we will ignore the glaring connection with string theory for now!!!!) Of course, the $64,000 question is how do we do this, since 23 = 8, not 10. I can provide a preliminary answer to this question, but whether or not it will be the prize winning answer remains to be seen. First, we need to understand that the 1331 = 8 numbers of the fourth line of the binomial expansion only have to equal 8. We don’t necessarily have to follow the equation of the binomial theorem, at least for now. So, another combination that equals 8 is 1421 = 8.
String theorists would look for a way to “hide” the missing two dimensions, in 3D space. We might be able to follow their lead and denote the fourth line as 14(4-2)1 = 1421 = 8, and say that two hidden dimensions are “compactified,” but then, we don’t have the same problem as they do, because we are not talking about dimensions of space, but rather dimensions of motion. So, we would say that two dimensions of motion are hidden, not two dimensions of space, which reminds us that Larson’s cube is an illustration of 3D motion, not 3D space.
As such, recall that Larson referred to the four diagonals in the 2x2x2 stack of one-unit cubes, which is not a 1331 map of the vector tetraktys. We are the ones who first mapped the 1331 tetraktys to the cube, by replacing the four orthogonal diagonals with the three orthogonal axes normally used in algebra and Euclidean geometry. In fact, we took our clue form GA, and paid scant attention to the difference.
But now, we find ourselves forced back to the four diagonals of Larson’s original cube, by the new discovery of the degeneracy in the three axes of the coordinate system view. This seems almost poetic, because it is the 8 units of 3D scalar motion of the RST that we are interested in, not the 8 units of the 1D vector motion of the LST! The diagonals of the stack of 8 cubes is again illustrated, as shown in figure 1 below:
Figure 1. The Four Diagonals of Larson’s Cube
Of course, the volume of the 2x2x2 stack of cubes is related to the volume of a sphere with a diameter equal to the length of the diagonals. Likewise, the area of a plane on the face of the stack is related to the area of a circle, with a diameter equal to the length of the diagonals. However, the scalar operation that generates a line from a point, and an area from a line, and a volume from an area, in scalar space, differs from the equivalent operation in vector space. In vector space, a line is generated from a point through translation, an area through translations of two objects, in independent directions, or through a rotation around an independent axis, and a volume through three translations, in independent directions, or a second rotation around another independent axis. These are the operations of addition and multiplication in vector algebra, the result of combining individual elements, considered as generated in one direction at a time, or by multiple objects in motion simultaneously.
In contrast, in our scalar space, a line is generated from a point through the expansion of the point, in two, opposite directions simultaneously, something that is impossible for a single object to do. An area is generated through the expansion of a line, in two, independent, opposing, directions, simultaneously, and a volume through the expansion of an area in two more, independent, opposing, directions, simultaneously. Thus, the four diagonals of the cube represent the 2, independent, opposing, directions, that the point can be expanded into a line, the 2, independent, directions that the line can be expanded into a plane, and the 2, independent, directions that the plane can be expanded into a volume, which is 23 = 8, independent, simultaneous, opposing, directions of expansion, in all, because the 2x2x2 stack of cubes is generated by simultaneous expansion in 2x2x2, opposing, directions.
In other words, the 3D scalar space is a 0D point expanded into a 3D sphere, not a set of 8, one-unit, cubes, generated individually and assembled together. Even though the end result is numerically equivalent, in both cases, the operations generating the multidimensional spaces are radically different. Hence, this implies that the meaning of the algebraic addition and multiplication operations, in the two different spaces, differ as well.
It seems clear that each, independent, 1D, diagonal of the sphere can be expanded into a 2D plane, in two, independent, ways. In one way, the line is expanded along the independent diagonal sloped in one direction, and in the other, it is expanded along the diagonal with opposite slope. Thus, there are four, independent, areas in the volume. Each of these areas can be expanded into a sphere by expansion in two, independent, opposing, directions to form the volume of the pseudoscalar.
Therefore, it appears, at least, that the scalar tetraktys is as faithful to the geometry of the sphere, as the vector tetraktys is to the geometry of the cube, and we can translate back and forth between them as required, in a clear and consistent fashion. If this turns out to be the case, the next step will be to identify the nature of the algebraic operations that can adequately express the expansion to higher dimensions, and the contractions to lower dimensions. I’m thinking that the dot symbol would work for the contraction operation (contracting toward a point), and the circle symbol would work for the expansion operation (expanding toward a sphere). We’ll see.