The Larson Research Center

In the previous entries below, we’ve discussed the concept of number, not as increasing/diminishing magnitude, but as order in progression, introducing an index of space|time progression, P_n, which we used to define a new set of natural, reciprocal, numbers, as a nested set of ordered sets:

{P₁}; {{P₁} {P₂}}; {{P₁} {P₂} {P₃}}; … {{P₁} {P₂} {P₃}…{PN₂}}

Next, we substituted these reciprocal numbers for the natural numbers of the tetraktys, showing how they provide a scalar version of what is normally interpreted as a vector (i.e. geometric) version of the binomial expansion. We did this on the basis of our identification of the binomial characteristic of the tetraktys, with the duality of vector direction, reasoning that the dual concept of scalar “direction” would provide a similar (isomorphic, or analogous) result, provided that we could find a way to define orthogonality in scalar terms.

Fortunately, it can be shown that the concept of scalar orthogonality, or independence of a combination of scalar values, is inherent in the combination of S|T units, as the preons of standard model entities, called S|T triplets, where the A, B, C, nodes of the triplets are independent reciprocal numbers. Thus, the scalar version of the tetraktys can be constructed, using the set of natural, reciprocal, numbers: 

(1/1)⁰

(2/2)⁰ (2/2)¹  

(4/4)⁰ {(2/2)¹ (2/2)¹} (2/2)²

(8/8)⁰ {(2/2)¹ (2/2)¹ (2/2)¹} {(2/2)² (2/2)² (2/2)²} (2/2)³

where the differences in the exponents are indices of dimensional symmetry; For instance, because 2/2 = 1/1 + 1/1, a one-dimensional degree of freedom is attained at P₂ = (2/2)⁰, relative to the “directions” at P₁ = (1/1)⁰, which are realizable as 1/2 or 2/1, representing two scalar “directions” analogous to the two vector directions of one-dimensional lines.

Similarly, at P₄ = P₂ + P₂, a two-dimensional symmetry is attained, since the product of P₂ with itself is (P₂)² (i.e. (2/2)*(2/2) = (2/2)² = (4/4). Likewise, at P₈, a three-dimensional symmetry is attained (2/2)*(2/2)*(2/2) = (2/2)³ = (8/8).

Thus, what we have in the scalar tetraktys is a binomial expansion of scalar “direction,” analogous to the binomial expansion of vector direction, and since the elements of the vector tetraktys can be regarded as the linear spaces, constituting the multivectors of GA, it is reasonable to conclude that a scalar algebra can be constructed over the linear spaces of the scalar tetraktys, as well.

With this much understood, however, it is recognized that there is a long way to go yet. In constructing GA, the first step is to define the geometric product, as consisting of the combination of the inner and outer product, where the inner product is a scalar, and the outer product is a vector (now called a bivector), and in this way describing the magnitude, or length, (inner product) and direction (outer product) of any vector in three spatial dimensions. This is very advantageous in GA, because the concept of vector is easily incorporated to express the complementary relation of kinetic and potential energy, or torque and work, or B field and E field, etc. in vectorial physics.

Of course, this was all accomplished without the benefit of GA, before it was uncovered by Hestenes. However, it was accomplished by means of what turned out to be subalgebras of GA, in the form of Gibbs’ vector algebra, and in the form of quaternions, disguised as matrices, and in the form of complex numbers, which are all subsumed by GA. Consequently, since the belated advent of GA, many physics applications have been rewritten in this language, applying it, not because the solutions were needed in any practical sense, but because they enable the central ideas and concepts of physics to be given a more intuitive, geometrical, interpretation, one which is much simpler and concise. 

We recognize this as a very propitious development for us here at the LRC, if we can use these applications, and the GA language used to describe them, to gain the crucial insight needed for the development of a scalar algebra (SA), suitable for doing physical calculations in RST theory.

The fact that Hestenes develops GA step by step in his book New Foundations for Classical Mechanics makes it the natural choice for our guide, but the fact that GA is a fomulation based on axioms, whereas our development can have no axioms, defines the biggest challenge in this approach. We first have to understand what the axioms are and how, and why, they do what they do in GA, before we can hope to see the way forward. That these axioms have to do with the operations, or the meaning, of multiplication and addition, in terms of one-dimensional vectors, bivectors, composed of vectors, and trivectors, composed of vectors and bivectors, while we have no vectors, bivectors, or trivectors, just scalars, and at the same time have discovered a definite and important meaning of addition, multiplication and division, in terms of our scalars, gives us a sense of the challenge: It is daunting.

To help us, it will be desirable to relate the scalar tetraktys to a scalar version of “geometry;” that is, we want to have a visual concept of the scalar analogs to 3D geometric entities, points, lines, areas, and volumes, as they relate to each other in the form of multi-dimensional, reciprocal, numbers. Of course, to do this, we return once again to Larson’s cube. This cube is called Larson’s cube, because he used it, in the course of defining scalar magnitudes, to show why the pseudoscalar has 2³ = 8 units of scalar magnitude, in a 3D system, not six, as some were want to argue. In chapter 12 of Nothing But Motion, he writes:

In three-dimensional space (or time) there can be two displacement units in each of the three dimensions, and the maximum three-dimensional unidirectional displacement is therefore 2³, or 8, units.

There have been some suggestions that the number of possible directions (and consequently displacements) in three-dimensional space ought to be 3 x 2 = 6 rather than 2³ = 8. It should therefore be emphasized that we are not dealing with three individual dimensions of motion, we are dealing with three-dimensional motion. The possible directions in a three-dimensional continuum can be visualized by regarding a two-unit cube as being an assemblage of eight one-unit cubes. The diagonals from the center of the assemblage to the opposite corner of each of the cubes then define the eight possible directions.

The cube, with its eight directions, as described by Larson, is illustrated below.

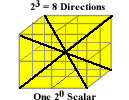
Figure 1. Larson’s Cube

Mapping the vector tetraktys to this cube, we can easily identify its multidimensional linear spaces with the geometric components of the stack of eight cubes, as illustrated in figure 2 below.

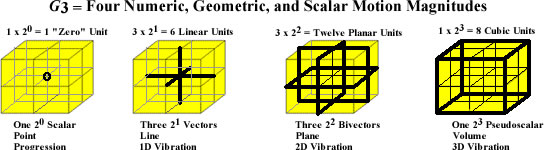
Figure 2. The Eight Dimensions of the Vector Tetraktys (1331) Mapped to Larson’s 2x2x2 Cube

The graphic in figure 2 was constructed several years ago and the text indicates our preliminary attempt to identify scalar magnitudes with vectorial magnitudes, but this attempt was premature and naive, so the reference to these concepts in figure 2 should be ignored. However, the figure does show how the linear spaces of G3, in GA, can be mapped to Larson’s cube. The first space contains 1 type of entity, the 0D scalars, analogous to a single geometric point, and is located at the center intersection of the 8 cube assembly. The second space contains 3 types of entities, the 1D vectors, analogous to three, independent (i.e. orthogonal), geometric lines, and is identified as the intersection of the horizontal and vertical edges of the eight cubes in the assembly. The third space also contains 3 types of entities, the 2D bivectors, analogous to three, independent (i.e. orthogonal), geometric planes, and is identified as the interface of the horizontal and vertical planes of the eight cubes. Finally, the fourth space contains 1 type of entity, the single 3D trivector, analogous to a unit cube, and is identified by the twelve outside edges of the assembly, forming its eight corners.

This geometric view of the vector tetraktys is helpful in mapping the scalar tetraktys as well, even though the “directions” of the scalar values have no geometric meaning; that is, the directions of vector distance magnitudes, and the associated directed numbers of GA, are isomorphic to the “directions” of scalar magnitudes, and the “directed” numbers of a future SA, but they are not identical. We might say that the geometric representation of the scalar tetraktys is symbolic of the scalar spaces in SA. In the graphic of figure 3 below, the scalar “directions” are indicated by colors, corresponding to the geometric directions of the cube, but the text of the graphic, referring to vibrations, is still erroneous and should be ignored.

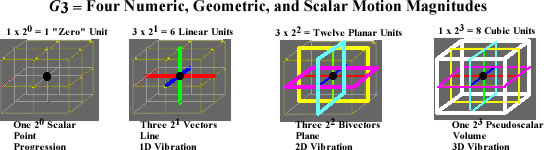
Figure 3. The Eight Dimensions of the Scalar Tetraktys (1331) Mapped to Larson’s 2x2x2 Cube

In this graphic, only the edges of the 2D and 3D magnitudes are colored for greater visibility, but the combinations follow the scalar concept faithfully, except, of course, in reality colors are mixed to obtain the “higher dimensional” color, not multiplied (actually, it amounts to the same thing, when you think about it - more on this later). Yet, the color black, in the scalar space, located at the origin of the cube, as a 0D scalar point, and the 1D primary colors, combining to form the 2D secondary colors, and these, combining together, or each in turn, with the “odd man out” primary, to form the 3D white color of the pseudoscalar, correspond perfectly to the linear spaces of GA, where

a; a,b,c; a^b, a^c, b^c; a^b^c

symbolize the k-blades of each linear space. It should be noted, however, that in our color scheme, the pattern of each color, denoting an independent dimension, should be altered to distinguish the polarities, or two “directions” above and below unity. In this way a striped color, for instance, could be used to indicate the opposite scalar “direction” indicated by the same, solid, color. This will be attempted when the image is updated later.

The important point is to recognize that the magnitude and direction of scalars, vectors, bivectors, and trivectors, in the vector tetraktys, are defined algebraically in GA, to provide an algebraic language, which is used to describe the magnitude and direction of multiple, one-dimensional, vectors, in the three-dimensional space of the cube. This is done, by defining a unit basis for each element of the space, and treating these as a righthanded, or dextral, set of basis vectors, interpreting the cube as a whole, with a bottom corner selected as the origin.

As Hestenes shows, scalar addition and multiplication are easily defined in this vector space, as is scalar multiplication of a vector. But scalar addition with a vector, an anathema to traditional approaches, is also defined, and is, in fact, the central feature of GA. In our case, however, we are not concerned with the magnitude and orientation of a combination of 1D vectors in a 3D space. Instead, we are interested in the configuration, we might say, or in the linear combination of the multi-dimensional components of the scalar tetraktys. This makes the location of the scalar space at the origin of the cube critical, for our purposes, because it preserves the proper tetraktys relation, between the scalar and the pseudoscalar, as reciprocal entities, in the algebra.

For instance, when the point at the center grows (“scales”), from (1/1)⁰ to (8/8)⁰, the cube becomes fully “populated” we might say, but when the scalar point is reduced from (8/8)⁰ to (1/1)⁰, for any reason, the cube is “depopulated.” Of course, the intermediate values play an important role as well. The objective seems to be to determine how these values might change, and what are the rules governing the changes. We already know that the periodic table can be generated by this process, so we are highly encouraged to pursue its investigation.

In the previous post below, we discussed the accepted concept of the natural numbers (which now days includes zero), as arising from Cantor’s abstraction of sets. This entails conceiving of something (the symbol Φ), which represents nothing, and counting it as something.

However, there is no need to resort to these shananigins, as can be seen from Hamilton’s early essay, known as the Algebra of Pure Time. Instead of considering numbers stemming from countable objects, Hamilton begins with order in progression, where a number is represented by moments in time, which can be either coincident, earlier, or later, when one is compared to the other. As we’ve noted before, this is the very ancient idea of fundamental order: Given that two numbers (or magnitudes) exist, one greater than the other, there will always be a third number (or magnitude) greater than them both.

Unfortunately, Hamilton got sidetracked by his pursuit of algebraic geometry, but a century later, Larson discovered the efficacy of thinking in terms of nothing but motion, when motion is defined as two, reciprocal, progressions, one a progression of time, and the other a progression of space. Order in progression then becomes the basis for all physical magnitudes, in terms of space and time speed-displacements, and, coincidently, all numerical values, in terms of operationally interpreted, reciprocal numbers.

In the case of numbers, we begin by noting that n/n = 1/1 = 1, and n|n = 0. When we consider that the eternal progression of the reciprocal quantities has no beginning and no end, then we can pick a starting point for a reference in which all past progression is not counted, and all future progression has not yet begun; that is, we abstract out a starting point in the progression, which we can designate P₀, from which point, everything is past, or future, in terms of both space and time progression.

However, in terms of a 3D space progression, “past” necessarily means smaller (less space) than P₀, while “future” necessarily means larger (more space) than P₀, but this requires that P₀ be picked out of an infinite set of possibilities, relative to the previous point, P_-1, since any point on the expanded sphere, relative to the origin, at P_-1, may be selected for P₀ (which is the foundation for the weirdness in quantum mechanics). Nevertheless, when considering numbers only, this is the difference between the scalar and the pseudoscalar, in the tetraktys, which difference is not apparent at the beginning of the tetraktys, where the dimension of the number is zero, because any dimensionless number (a number raised to the power of 0) is equal to 1.

Thus, (n/n)⁰ = 1⁰/1⁰, and, in a progression ratio, this is how we represent the unit ratio, a ratio of unit scalars. However, when we choose a reference point in the progression, P₀, then, at this point, before the next step in the progression occurs, the progression count is zero. After one unit of progression occurs, the progression count is one, and so on giving us a series, P₀, P₁, P₂, …P_n, where P₀ = (0/0)⁰, P₁ = (1/1)⁰, P₂ = (2/2)⁰, …P_n = (n/n)⁰.

If this seems a little like spinning wheels, it is. There is no numerical difference between these steps, since any number, raised to the power of zero, has the same value as any other number raised to the power of zero. Yet, obviously, as the progression continues, the point, P_n, is much greater than the point, P₀, in terms of the number of steps of progression. 

The minimum number of steps of progression that we can perceive, from P₀, is one, but there is no maximum, because, in an eternal progression, there is always a next step, ad infinitum. But just as Hamilton based his numbers on “steps,” in the relative values of temporal progression, we can comprehend steps of reciprocal progression in terms of relative values. In one step, 1/1, there is no variability, but in two, or more, steps, there certainly is. That is, in one step of the progression, (1/1)⁰, there is no freedom, but in two steps, (2/2)⁰, there is an increased degree of freedom.  The question is, therefore, what are the consequences of this increase in freedom?

The answer is obvious, but profound, as Hamilton discovered, when he developed his time steps into numeric couples. Interestingly enough, though, as Hamilton developed the ideas of steps and couples, in the order of temporal progression, with its concept of change, as a central notion, Grassmann was discovering the meaning of dimension in numbers, which corresponds to dimension in space, with no concept of change involved. Neither one of these two geniuses understood their work in terms of the tetraktys, as we now do, but Hamilton loved the mystery of the tetraktys, even writing a poem to it, alluding to his quaternions.

THE TETRACTYS

Or high Mathesis, with her charm severe,
   Of line and number, was our theme; and we
   Sought to behold her unborn progeny,
And thrones reserved in Truth’s celestial sphere:
While views, before attained, became more clear;
   And how the One of Time, of Space the Three,
   Might, in the Chain of Symbol, girdled be:
And when my eager and reverted ear
Caught some faint echoes of an ancient strain,
   Some shadowy outlines of old thoughts sublime,
Gently he smiled to see, revived again,
   In later age, and occidental clime,
     A dimly traced Pythagorean lore,
     A westward floating, mystic dream of FOUR.

However, in the work of Clifford, the power of the tetraktys would begin to emerge, as he brought the work of Hamilton and Grassmann together, combining the two in a fashion that would eventually lead to a new way of viewing numbers, the power of which was not fully appreciated, until Hestenes empahsized it.

Yet all this seemed so irrelevant, as Dedekind looked to understand real numbers, and he and Cantor eventually took the path of formulating axioms, leading to set theory and modern mathematics. Even today, though geometric algebra (GA) seems to live in the fullness of the tetraktys, thereby subsuming the algebras of the reals, the complexes, and Hamilton’s quaternions, the preoccupation of mathematicians, with set theory and group theory and the associated notions of topology and category theory, appears to have blinded their minds, in part at least, to the power of the tetraktys, in spite of the tremendous clues, given by GA and Raul Bott.

To appreciate this power takes a willingness to understand the advantages of the intuitive notion of order in progression, as Hamilton (encouraged by the writings of Kant) first dared to entertain them.  Later, Larson (encouraged by the writings of Samuel Alexander), enlarged upon the ideas of Hamilton (though there’s no indication that he knew of them), by assuming that space, like time, is a natural progression, identical in every respect to the time progression, but the reciprocal of it.

When we take these ideas and apply them to the tetraktys, we can develop a set of natural numbers, where the first set is

{P₁ = (1/1)⁰}

and the next set is

{P₂ = (2/2)⁰}

which consists of two steps, identical to P₁. Hence,

P₂ = P₁+ P₁

P₁ being the progression step from P₀ to P₁ and P₂ being the progression step from P₁ to P₂.  

Applying this to the tetraktys, we get

{P₁}
{P₂ P₂}

or,

{1/1}
{{2/2} {2/2}}

the geometric interpretation being a point in the first set and two double points in the second set, or

{(P₁)⁰}
{(P₂)⁰ {(P₂)¹}}

since two, zero-dimensional, points are free to form a one-dimensional line.

However, here we are deviating from the usual interpretation, with regards to the scalar (on the left) and the pseudoscalar (on the right). In this interpretation, the difference in their dimensions indicates that one is the inverse of the other; that is, in the first line of the tetraktys the element of the set is its own inverse (1/1 = 1/1), but in the second line of the tetraktys, the inverse is one dimensional (2/2 = (1+1)/(1+1), as in reflection symmetry and the commutative law.

On the same basis, the third set is then

{P₃ = (3/3)⁰}

where

P₃ = P₂ + P₁

which, in one-dimension, is a combination of a point on a line, recognizing that two, independent, lines are required for two dimensions, which independence we don’t attain until P₄, forming the fourth set: 

P₄ = P₂ + P₂

or

{(P₁)⁰}
{(P₂)⁰} {(P₂)¹}
{(P₄)⁰ {(P₄)¹} (P₄)²}

Of course, all P_n, greater than P₁, are combinations of P₁, or multiples of P₁, but again, the independence, this time of both points and lines, enables the formulation of higher dimensions, in a progression of degrees of freedom, characteristic of the tetraktys. The freedom is the freedom in the order of progression, where one step is either coincident, earlier, or later than another. In other words, it increases as the power of 2, or 2ⁿ, beginning with 0. That this is nothing more than the inherent property of direction is easy enough to recognize, but what must be recognized now is that it is also the inherent property of “direction” (see previous post on this).

With this much understood, we can substitute the idea of “direction” for the idea of direction in the tetraktys. On this basis, P₂ represents two “directions” along a line, rather than two points, forming a line; that is, with two units of progression, two polarities of a single line can be represented, or the “distance” between two polarities is analogous of the distance between two points. Hence, 1/2, or 2/1, are two values, or “directions” that are inherent in P₂ = (2/2)¹, just as two directions (left or right, up or down, or back and forth) are inherent in a line between two points.

At the same time, these two, inherent, “directions” are not realized in P₂ = (2/2)⁰, and not realizable in P₁ = (1/1)⁰. Therefore, in P₃, the only “directional” possibility is 1/2 and 1/1, or 2/1 and 1/1, analogous to the “distance” from a point to the 1/2 value, or from a point to the 2/1 value, in the other “direction,” with the point located between the two values. This is reminiscent of the ancient Greek idea that three was the first number, it being the perfect number, representing the reunion, or perfection, of duality, which must split unity.

However, as Hamilton discovered, three does not have sufficient power to reach the next higher dimension.  Only at P₄, is there sufficient freedom to reach the next higher level, the third dimension, of the tetraktys (counting 0). We can see this as extending the freedom of P₃, where the “direction” from point to 1/2, or 2/1, goes from a point to 1/2 AND 2/1, because the total number of units now makes this possible, whereas before it didn’t:

P₄ : 4/4 - 1/2 = 3/2, and 3/2 - 2/1 = 1/1

Now, there are sufficient units to combine both the two separate “directions” and the point into one dual “direction,” relative to the point, in terms of reciprocal numbers, but at P₃ there is insufficient magnitude to join them together through a point in the middle, so-to-speak:

P₃ : 3/3 - 1/2 = 2/1 

Likewise, at P₅, P₆, and P₇, there are an insufficient number of P₁s to form the next level of the tetraktys, which requires two P₄s, which is predictable enough, since the second dimension requires two P₁s, and the third requires two P₂s. This is easier to track if we use actual numbers.  The full tetraktys looks like this:

(1/1)⁰

(2/2)⁰ (2/2)¹  

(4/4)⁰ {(2/2)¹ (2/2)¹} (4/4)²

(8/8)⁰ {(2/2)¹ (2/2)¹ (2/2)¹} {(4/4)² (4/4)² (4/4)²} (8/8)³

There is much more to be explained, but this will do for now.

As mentioned before, one the most surprising (and gratifying!) discoveries made in connection with the new system of mathematics (the RSM), is the work of Sir William Rowan Hamilton, in regards to his early efforts to develop a science of progression, which he called a science of pure time. It turns out that, while this was very significant in the history of mathematics, because it lead to a new understanding of complex numbers, the concept of a vector (even the word), and the discovery of non-commutative quaternions, the novel ideas of Hamilton, regarding the advantage of the concept of order in temporal progression, rather than the concept of increasing and diminishing magnitude, as a basis for natural numbers, it was never accepted by the mathematical world, and remains an obscure footnote of history to this day.

In fact, Hamilton himself abandoned the conviction that this “strange theory” was a promising approach to an a priori intuition, revealing the natural fount of mathematical truth. In the end, he gave up the quest for an intuitive science of pure time, and turned to the more popular mathematical formalism, which found its ultimate expression in the work of the younger Dedekind and Cantor, who established the basis of modern set theory and set the course for the runaway formalism that is the bane of modern theoretical mathematics and physics, in my opinion.

Nevertheless, Hamilton’s use of “couples,” based on what he called “steps” in the order of progression, enabled him to validate the concept of negative numbers, algebraically, without recourse to geometry (which he regarded as the science of space) and the idea of rotation. In his words, his algebra of pure time “[removed] the difficulties of the usual theory of negative and imaginary quantities…”:

As already pointed out, though, Hamilton gave up the promise of this early intuition-based approach, and joined the ranks of formalists, like Peacock, after his discovery of quaternions. However, had he had the benefit of Larson’s insight, that his preferred basis of numbers, as intuitive-based values, emerging from the order in the temporal progression of nature, belongs not only to pure time, but to pure space as well, in a reciprocal relation, as pure motion, the subsequent history of mathematics and science would most assuredly be radically different.

We have seen that the simple operational interpretation (OI) of rational numbers, when combined with the idea of two, reciprocal, progressions, does indeed lead to an intuitive concept of positive and contrapositive numbers that are “free from those difficulties…derived from the bounded notion of magnitude.” We have discussed the two groups, one under addition, and one under multiplication, which these positives and contrapositives form, corresponding to magnitudes, which at once have both discrete and continuous properties.

We have identified the algebraic properties of these numbers and identified the correspondence with physical magnitudes of geometry, in the tetraktys, wherein the geometric points, lines, areas, and volumes correspond to numerical values, at least in terms of the scalar spaces that can be mapped to vector spaces.

We have also discussed Hestenes’ views regarding the Clifford algebras of these Grassmann spaces, especially with respect to his Geometric Algebra (GA). Through all this, it seemed clear that we were on the verge of uncovering a new, scalar, algebra that would be a complement to the vector algebra of GA, an exciting prospect indeed. However, trying to fit the three dimensions of OI numbers, into the tetraktys, while numerically revealing in many ways (see Chart of Motion), has proven difficult from a geometric standpoint, because while the red, green,and blue colors that we employed for this purpose, are good scalar analogs of discrete scalar motion magnitudes, they are not good vector analogs of points lines, areas, and volumes.

Since there was no immediate need to bridge this gap, it was more or less pushed into the background, but it comes to the foreground in trying to work out the mathematics of the standard model preons.  The question is, how do we map the three scalar magnitudes, of the scalar tetraktys, represented as red, blue and green “directions” of the scalar reference system, to the three vector magnitudes, represented as the x, y, and z directions of the spatial reference system?

It seems, intuitively, that this is a necessary task, but the advantages, algebraically, are marvelous, since such a correspondence would give us a map to a space|time algebra, based on known principles of vector algebra, but free from the pathologies in those algebras that stem from the loss of algebraic properties such as order, commutativity, and associativity, which make the complex numbers philosophically difficult, the quaternions neurotic, and the octonions, the “crazy uncles” of the mathematical family, so unfit for polite company that the mathematicians keep them locked up in the attic, as described in John Baez’s account of the four normed division algebras:

The real numbers are the dependable breadwinner of the family, the complete ordered field we all rely on. The complex numbers are a slightly flashier but still respectable younger brother: not ordered, but algebraically complete. The quaternions, being noncommutative, are the eccentric cousin who is shunned at important family gatherings. But the octonions are the crazy old uncle nobody lets out of the attic: they are nonassociative.

The answer, seems to be in understanding the definition of independence, or orthogonality, both in terms of numbers and in terms of physical magnitudes. This is the meaning of dimension. Each independent dimension has two directions in the vector space, while each independent dimension has two “directions” in the scalar space, where the difference between direction and “direction” is the difference between direction of distance, ds/dt * t, and “direction” of polarity, ds/dt:dt/ds. However, direction has no meaning in the scalar space of positive and contra-positive magnitudes, and “direction” has no meaning in the vector space of distance between two points. Thus, directional orthogonality is not the same as “directional” orthogonality.

However, in vector space, there are three, and only three, orthogonal dimensions, each with its two directions, which can be interpreted in polar terms, but, in scalar space, there is one, and only one, dimension, with two polar “directions.” Nevertheless, there is an additional, orthogonal, dimension of sorts in scalar magnitudes, with one “direction.” It is the total number of positives and negatives. We have been considering these three scalar “directions,” as three scalar dimensions, and mapping them to the tetraktys, but this proves to be problematic, ultimately, when we consider the tetraktys in terms of the properties of physical magnitudes; that is, the binomial expansion of the tetraktys reflects the directional duality of the three dimensions of physical magnitudes, not the “directional” triality of two scalar dimensions! 

It’s true that we can assign three primary colors to each of these scalar “directions,” as if they were independent dimensions, and when we do the colors combine in an impressive way, as we’ve seen, but in the end, we sense that there is something wrong with identifying the third “dimension” with the total units of the scalar entity, even though it seemed the only reasonable alternative, until recently.

However, with the emergence of the S|T triplets, and the ideas of meshed gear ratios, which have become the center of so much attention here at the LRC, during the Summer and Fall months, it has become obvious that another identification of three scalar dimensions is possible, which has none of the former difficulties. These are the three nodes, the three “gear ratios,” of the S|T triplets, designated A, B, C (and D, the internal mode, which we haven’t discussed much yet). 

It’s somewhat ironic, I think, that the best way to understand the mathematical content of all this might be to consider it from what might be loosely called a set theoretical point of view; that is, if we start at the beginning, with the initial set of numbers, and work our way forward, to develop the idea of number, as a set, the power of the logic will be clearly evident. This is the way it has historically been approached, but from the standpoint of quantity and increasing/diminishing magnitudes, which Hamilton found so wanting.

For instance, in his book Road to Reality, Roger Penrose, explaining what we mean by natural numbers, integers, rationals, etc, asks the question, “Do natural numbers need the physical world?” His answer begins by noting that zero is included among the natural numbers today, but was not included by the ancient Greeks. He writes:

The natural numbers are the quantities that we now denote by 0, 1, 2, 3, 4, etc., i.e. they are the non-negative whole numbers….the role of the natural numbers is clear and unambiguous. They are indeed the most elementary ‘counting numbers,” which have a basic role whatever the laws of geometry or physics might be. Natural numbers are subject to certain familiar operations, most particularly the operation of addition and multiplication, which enable pairs of natural numbers to be combined together to produce new natural numbers. These operations are independent of the nature of the geometry of the world. 

But this definition would have irked Hamilton to no end. It was his conviction that, while the science of numbers is “independent of the nature of the geometry of the world,” all right, it still has to have a connection with the properties of the physical universe, which is just as essential to the science of numbers, as is the connection of physical space to the world, in the science of geometry. If numbers have a “basic role in whatever the laws of geometry or physics might be,” that role had to somehow be conceived, as rational and intuitively derived, starting from observation of the structure of the physical universe, as it is in geometry.  

But Penrose doesn’t think so: “There are various ways in which natural numbers can be introduced in pure mathematics and these do not seem to depend upon the actual nature of the physical universe at all,” he asserts. In other words, the formalist worldview, omnipresent in the minds of mathematicians today, doesn’t demand the intuitive basis that Hamilton sought. The only requirement is to think in terms of an abstract notion, Penrose explains. Although fraught with philosophical difficulties, “natural numbers can be introduced, merely using the abstract notion of set,” he writes.

Penrose goes on to show how Cantor, the father of modern set theory, developed the concept of natural numbers from the notion of set, which leads to definitions of set properties such as cardinality and ordinality. The simplest set of all, explains Penrose, is the empty set:

It is characterized by the fact that it contains no members whatever! The empty set is usually denoted by the symbol Φ, and we can write this definition

Φ = { }

where the curly brackets delineate a set, the specific set under consideration having, as its members, the quantities indicated within the brackets, so the set being described is indeed an empty set.

It’s interesting to note that, while physicists used to employ the notion of an empty vacuum, they now need to define a vacuum as teaming with virtual particles, but mathematicians, who used to begin with something (the Father of all was the number 1 for the ancient Greeks), they now need to define something as nothing. We can easily imagine the extent of consternation Hamilton would have no doubt felt over this modern perplexity of fundamental notions in physics and mathematics.

Penrose goes on to define natural numbers, beginning with 0, using the notion of set:

Let us associate Φ with the natural number 0. We can now proceed further and define the set whose only member is Φ; i.e. the set {Φ}. It is important to realize that {Φ} is not the same set as the empty set Φ. The set {Φ} has one member (namely Φ), whereas Φ itself has none at all.

Then, by combining these initial two sets of Φ and {Φ}, equivalent to 0 and 1, into a third set, the number 2 is defined as a set with two members. In the same way, by combining these three sets into a new set, a set of three is defined, and so on, ad infinitum. Penrose then observes:

This may not be how we usually think of natural numbers, as a matter of definition, but it is one of the ways that mathematicians can come to the concept….Moreover, it shows us at least, that things like the natural numbers can be conjured literally out of nothing, merely by employing the abstract notion of ‘set.’ We get an infinite sequence of abstract (Platonic) mathematical entities - sets containing, respectively, zero, one, two, three, etc., elements, one set for each of the natural numbers, quite independently of the actual physical nature of the universe.

To Penrose, the idea that an infinite sequence of numbers can be “conjured” up out of nothing like this, purely by means of the human mind, without recourse to the structure of the physical universe, is quite mysterious, because it is obvious that “‘real numbers’ indeed seem to have a direct revelance to the real structure of the world.” He notes in this context that in his preface to the book he discusses the subtle impact the mysterious nature of numbers may have on those who are convinced that they have no ability to comprehend math. That many times they believe that they cannot even fathom fractions, “with all that cancelling,” gives Penrose pause. He points out that there may be more to this difficulty than meets the eye, because, after all, there is something very mysterious about the fact that n/n = 1, although he is not able to go beyond merely noting it.

This actually paints a most dramatic scene before us, given our knowledge of the importance of n/n = 1 and how easily the number 1 can be developed into a complete system of reciprocal numbers, with both discrete and continuous properties, and given Hamilton’s work, where a world-class genius acknowledges the power of its intuitive connection to nature, through its central concept of order in temporal progression.

So with this scene as our prologue, we will proceed next to use this idea of sets in a new way, as directly connected to the structure of the physical world, instead of conjuring it up out of the imaginations of our minds, turning the science of mathematics from the inventive science of the Formalists, or, as Hamilton would have called them, the Philologists, to the inductive science of the Intuitionists, or, as Hamilton would have called them, the theoriticians.

We’ve been discussing the two groups of operationally interpreted (OI) reciprocal numbers. The group under addition is isomorphic to the group of integers, under addition, and the group under multiplication is isomorphic to the group of nonzero rational numbers, under multiplication.

The binary operations of these two groups is actually subtraction, symbolized by the pipe symbol, “|”, and division, symbolized by the usual slash symbol, “/”. As the properties of these numbers differs substantially from those of the integers and rational numbers, we need to designate them some way that will help us refer to them uniquely.

The easiest way to to do this, although probably not the best way, is to resort to acronyms. Accordingly, we will refer to the difference interpretation of reciprocal numbers as DRNs, and the quotient interpretation as QRNs.

The two, different, OI magnitudes of the hypotenuse of the right triangle, with sides a = b = 1, are shown in figure 1 below.

Figure 1. The Geometry of QRN and DRN. Two Operational Interpretations of a Unit Reciprocal Number

While the zero evaluation of the hypotenuse might seem strange at first, when it clearly has a definite length, this difficulty can be overcome, when it is noted that, here, the number c is not necessarily a measure of the length, but of the relative angles, of the hypotenuse. The difference value obtained is tantamount to measuring the difference between the two acute angles of the right triangle. When these angles are the same, we may say that their difference is 0, just as legitimately as we may say that they are identical.

Taking the unit triangle, and its two OI values, as the genesis of a discrete number system, there are two, and only two, unit increments possible. These are:

1. 1/2 = .5, or 1|2 = -1
2. 2/1 = 2, or 2|1 = 1

In the DRN value, the unit increments are linear (-1, 1), while in the QRN value, they are not (.5, 2), even though the change in geometry is identical in both cases, as shown in figure 2 below:

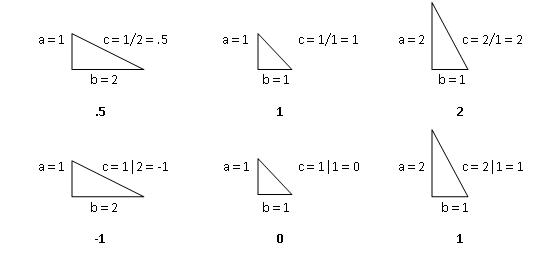
Figure 2. The Two Possible Unit Increments of the Unit Triangle

It’s easy to see that a set of DRNs, consisting of all combinations of 1|2 = -1 and 2|1 = 1, is a representation of a group under addition, isomorphic to the set of integers, which is a group under addition: Let D be the set of DRNs, n|n, 1|n, n|1, where n is a positive whole number. The subset of 1|n = {…, -4, -3, -2, -1, 0}, and the subset of n|1 = (0, 1, 2, 3, 4, …}. Let the symbol “+” indicate the operation of addition. Then (D,+) is a group. The proof is:

Closure : If a and b are DRNs then a + b is a DRN.

Associativity : If a, b, and c are DRNs, then (a + b) + c = a + (b + c).

Identity element : 0 is a DRN and for any DRN a, 0 + a = a + 0 = a.

Inverse elements : If a is a DRN, then the inverse DRN, −a, satisfies the inverse rules: a + (−a) = (−a) + a = 0.

In the case of QRNs, consisting of all combinations of 1/2 = .5 and 2/1 = 2, these form a set that is a representation of a group under multiplication, isomorphic to the set of nonzero rationals, which is a group under multiplication: Let Q be the set of QRNs, n/n, 1/n, n/1, where n is a positive whole number. The subset of 1/n = {…, .2, .25, .33…, .5, 1), and the subset of n/1 = {1, 2, 3, 4, …}. Then (Q,*) is a group. The proof is:

Closure : If a and b are QRNs then ab is a QRN.

Associativity : If a, b, and c are QRNs, then (ab)c = a(b c).

Identity element : 1 is a QRNI and for any QRN a, 1 * a = a * 1 = a.

Inverse elements : If a is a QRN, then the inverse QRN, a, satisfies the inverse rules: aa = aa = 1.

One of the many interesting aspects of this development is that the group of QRNs contains an infinite number of finite subgroups of order (2n)-1, where n/n is the identity element of the group. As figure 2 above shows, this is akin to dividing the unit circle into parts, from 0 to 1 and from -0 to 1.  As pointed out in the previous post, if we regard 1 as π radians of rotation, then the finite QRN groups are tantamount to a subset of rotations of size n. In essence, we are dividing the unit circle into clockwise and counterclockwise rotations.

For example, when n = 2, the identity element is 2/2 = 1, and the other elements of the subgroup are 1/2 = .5 and 2/1 = 2, which are actually two, equipollent, intervals between -0 and 1, and 0 and 1, respectively. This is what enables the rotation representation, as clockwise and counterclockwise rotations from 0 to π. However, to recognize this point, it is necessary to understand how .5 and 2 can constitute -0 and 0, respectively, when the denominator, or the numerator, of the identity QRN, 2/2, is reduced from 2 to 1; that is, we don’t increment one side of the initial unit triangle from 1 to 2, as in figure 2, but we start with a two-unit triangle and reduce one side to 1 unit.

In the RST, this is a consequence of “direction” reversals, because there are two half-cycles in each cycle of oscillation.  However, when we just deal with numbers, we are accustomed to adding one discrete number to another, since there is no physical constraint to prevent this.  Yet, in the RST, we can’t just add a unit of time, or a unit of space, to the unit progression, to obtain ds/dt = 1/2, or 2/1, because units of space and units of time are not independent entities, but they are nothing more than the reciprocal aspects of the same entity.

Thus, the only way ds/dt can change from 1/1 to 1/2 or 2/1, physically, is for the progression “direction” reversals to take place over two cycles, effectively reducing one aspect, or the other, from 2 increases every two units, to one increase every two units. Of course, from the number perspective of physical magnitudes, it makes no difference how we get to 1/2, or 2/1, these values are simply possibilities, but from the progression perspective, we arrive at the conclusion that only 2/2 has these possibilities, intuitively. 

Indeed, from the progression perspective, we see that a decrease offsets an increase, so the only way to get to the 1/2, or the 2/1, space|time progression ratio, in the RST, also effectively halts the increase in the reversing aspect.  Like a soldier marching “in place,” the “direction” reversals effectively reduce the space, or time, progression from unit progression, to zero progression, in the reversing aspect.  This is clearly demonstrated in the progression algorithms and the world line charts, here and here.

However, within additional units of progression, it’s possible to divide the pie into additional pieces, as it were.  Thus, when ds/dt = 4/4, there are twice as many units of space and time available to form units of displacement, or elements of the subgroup:

1/4, 2/4, 3/4, 4/4, 4/3, 4/2, 4/1

Therefore, with n/n, we obtain n-1 negative and positive elements, and the identity element is still 1, because n/n is always equal to 1. However, to meet the closure requirement of the group, we have to include x dimensions of elements.  I’m sure the mathematicians will recognize this and have a name for the notion, but with my limited knowledge of groups, the only way that I can describe it is with the notion of x dimensions.

On this basis, for example, (1/4)*(1/4) = 1/16, or 1/4², which is an element of the group, so that the group elements are n⁰/n⁰, n¹/m^x, and m^x/n¹, where n and m are positive whole numbers, m > n, and x = 1 -> ∞. This follows from the fact that the denominator in the negative elements of the subgroup, and the numerator in the positive elements of the subgroup, will always be factors of m. I’m not sure what this does to the order of the group, or whether this means that the subgroups are infinite after all.

I’ve yet to contemplate the consequences of all this, or even to validate it completely.  I may have to stand corrected, at some point, but right now it seems that this approach gives us the intuitive route to the ad hoc formalism used in quantum mechanics.

The importance of groups in mathematical physics is hard to overstate. A group is defined as a set of elements with a binary operation that conforms to the laws of a group, which include certain algebraic properties and the notion of an identity element that relates to the reciprocal elements of the group in a specified way.

Here at the LRC, we have discovered that the reciprocal numbers of our new system of mathematics are group representations. These consist of two operational interpretations (OI) of reciprocal numbers: The first OI number is the difference relation of the reciprocal number that is isomorphic to the integers, a|b, and the second is the quotient relation that is isomorphic to the non-zero rational numbers, a/b.

We’ve seen that the first generates a number system, with 0 as the identity element, and the second generates a different number system, with 1 as the identity element. The former is a representation of a group under addition, while the latter is a representation of a group under multiplication.  We have seen how the SUDRs and TUDRs are combined as elements of the additive group, forming SUDR|TUDR (S|T) combos, and how these S|T units combine as elements of the multiplicative group, forming S|T triplets, which have the properties of spin, charge, and mass, observed in the standard model of particle physics.

Of course, the particles of the standard model are based on complex numbers and rotation in the complex plane, in what is known as gauge theory, while the S|T units are based on the reciprocal numbers that are generated by the “direction” reversals of the RST. Obviously, the straightforward concepts of the RST stand in stark contrast to the esoteric concepts of gauge theory, but the two approaches have to be related somehow, if both are valid to some extent.

The connection is enlightening.  While the LRC investigations of the RST have revealed that the multidimensional magnitudes of motion shown in the chart of motions are fundamental modes of motion that don’t include rotational motion, it is also clear that rotational motion has enabled LST physicists to progress without recognizing the principles inherent in the chart of motion; that is, they have been able to construct their theories on one-dimensional magnitudes, by resorting to the two-dimensional rotation of the complex plane.

In the past, we’ve discussed how this works from a physical perspective, since frequency, 1/dt, is actually a velocity, ds/dt, considered as a rotation. However, recognizing that the unification of binary sums and products, via the OI reciprocal number representations of the two, reciprocal, groups, under addition and multiplication, dramatically shows how this is possible from a mathematical perspective.  

Recall that the identity element of the additive group is 0, resulting in an infinite expansive system,

-n, …, -1, 0, 1, …, n

while the identity element of the multiplicative group is 1, resulting in the reciprocal, infinite, contractive system,

-0. …, 1, …, 0 

where the order of a given finite subgroup depends on the reciprocal number n|n = 1|1 = 0, or n/n = 1/1 = 1. In the additive group, then,

-1 + 1 = 0, and 1 -1 = 0,

while in the multiplicative group,

.5 x 2 = 1 and 2 x .5 = 1,

when n = 2. Thus, in the binary operations of the two groups of order 2, the sum is equal to the product; that is,

2+2 = 4, and

2x2 = 4 

The question is, why is this significant? And the answer is that it reveals the mathematical connection between rotation and vibration, or between the standard model’s gauge theory, and the LRC’s S|T theory.  To understand this it is only necessary to recognize that the reciprocity of the two representations of OI reciprocal numbers, which makes them dual to one another, is inherent in the rotations of the complex plane as well.

This is seen, in the first instance, by rotating from zero to π in one of two “directions,” positive, or negative:

-π, 0, π

or rotating from π/2 to 2π:

π/2, π, 2π

What the complex number did was give the LST physicists the ability to define an infinite expanse of numbers in the first case, and an infinite contraction of numbers in the second case. On this basis, they can construct representations of the same two groups that we have constructed using OI reciprocal numbers. In the first case,

-π + π = 0, and π - π = 0. and in the second case,

.5π x 2 = π, and 2π x .5 = π 

Clearly, then, this implies that the ad hoc invention of complex numbers is no longer needed.  We should be able to do quantum physics without complex numbers and the formalism that is based on them.  Time will tell, but certainly these insights are encouraging indications.

Addendum:

To be more explicit, the above analysis for the multiplicative group of π rotations requires that the identity element be 2π/2π = 1/1 = 1. In other words, when we use the reciprocal number identity element, n/n = 1/1 =1, n is the order of the finite subgroup (the number of elements in the subgroup, not counting the identity element). In this case, we are choosing n = 2. The elements of this subgroup are therefore

π/2π, 2π/2π, 2π/π = .5, 1, 2,

which, as shown previously, is taken to be

-0, 1, 0, 

under the quotient OI. In gauge theory, this would be equivalent to a phase shift, where the identity element is “unit” phase, and the inverse elements are 180 degrees out of phase in opposite “directions.”