The New Mathematics
Calculating the Diameters, Areas and Volumes of SUDRs & TUDRs
In the last entry, we discussed the mathematics of Larson’s cube (LC) and saw how one can calculate the ratios of the associated inverses, based on a 2D number system, using the square root of 2 and its inverse, analogous to the linear number system based on 1 and its inverse, but incorporating a change in the constant of proportionality.
Hopefully, this new ratio will prove useful, but we can extend it to the two balls that are defined by the LC. The diagonal of a 1x1x1 cube is the square root of 12 + 12 + 12 = 3, and since the radius of the outer ball of the unit LC is the diagonal of the unit cube, then we can use this radius and its inverse as the basis of the 3D number system, and the corresponding tetraktys.
To extend the inverse numbers, defined by the inverse LC to infinity, we simply calculate the reduction of the length of the sides of the current cube by the 45 degree rotation of its side to obtain the side length of the new cube, and then multiply this number by the square root of 3 to get the reduced radius and plug it into the appropriate formula for the diameter, surface area and volume of the ball.
This gives us a 3D number line, analogous to the 1D and 2D number lines we have already compared:
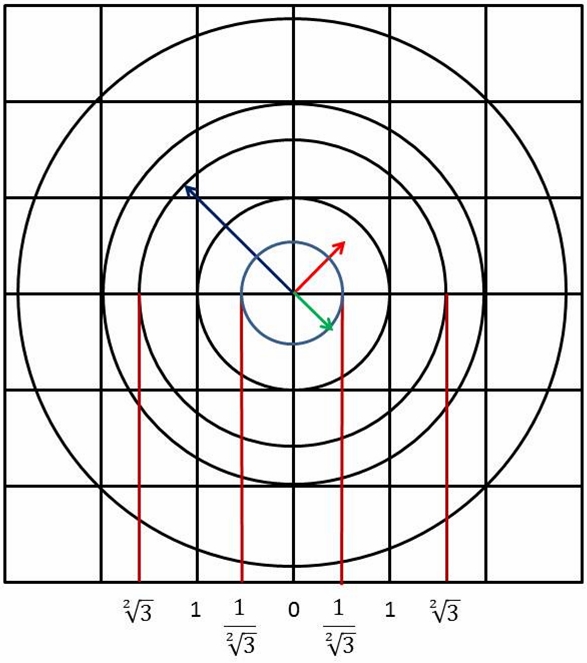
Figure 1. The the Right Lines and Circles of the 3D Number Line.
It’s important to note that the projected radius of the 3D outer ball is larger than the radius of its 2D cross section counterpart, since its actual third dimension must be large enough to just contain the eight corners of the unit LC. However, if the larger radius (31/2) were actually rotated out of the page, into the third dimension, it’s clear that it would appear to shrink to the 2D size of the cross section (21/2). Therefore, the 2D projection, or representation, of the 3D outer radius is actually larger than the boundary of the unit cross section.
The inverse is true for the inner ball: Its 2D representation must be smaller than the 2D boundary because its unit length is rotated out of the page and projected onto the cross section from above it. Hence, to show the true length on paper, the outer 3D radius is rotated onto the page, increasing the length of its projection onto the cross section, while the inner 3D radius is rotated out of the page, decreasing its projection onto the cross section.
It was this nuance that escaped my notice and introduced errors into the calculations that I was pursuing earlier.
More later.
Discrete Magnitudes of Right Lines & the Analog Magnitudes of Circles
Things are moving quite fast in the LRC development of the RST. I hope and pray that the Peter Principle doesn’t overcome us, before we can explain the atomic spectra, which is our immediate research goal. Mathematically and geometrically, we are focused on two things and their relationship: These two things are the geometrical set of right lines and circles constructed with Larson’s Cube (LC), and the algebraic set of numbers in the tetraktys, generated by the binomial expansion.
Given Sir Hamilton’s complaint that the science of algebra pales in comparison to the science of geometry, which we have referred to often, it is gratifying that we have discovered that the tetraktys is a mathematical map of the LC. That is to say, the numbers of the tetraktys correspond to the lengths of the right lines in the LC’s 2x2x2 stack of unit cubes:
- 20 = 1 = 0D unit expansion of LC (point)
- 21 = 2 = 1D unit expansion of LC (Line)
- 22 = 4 = 2D unit expansion of LC (Area)
- 23 = 8 = 3D unit expansion of LC (Volume)
This correspondence of the numbers of the tetraktys with the geometry of Larson’s cube is highly significant, since the LC not only contains the discrete magnitudes of the geometric cubes, but also the continuous magnitudes of the geometric balls.
Indeed, the LC contains the new number line, in the form of nested right lines and circles, which we have been investigating in light of the 4n2 numerical patterns of the wheel of motion, especially in light of the Le Cornec findings.
In the previous post, we discussed the two operational interpretations of the rational numbers, the quotient interpretation and the difference interpretation and how there are two units involved: One unit, 1/2, is the inverse of the other, 2/1, which are the units of the LC, and its inverse, but also the corresponding units of the SUDR and TUDR, respectively.
Since the SUDR is the 3D oscillation of space/time, while the TUDR is the 3D oscillation of time/space, this means that the magnitude, or the speed, of the TUDR is four times greater than the magnitude, or speed, of the SUDR. This was troublesome actually, because the number of preons in the S|T triplets depends upon a 1:1 relative weight between the two.
However, we recognize that, from the perspective of unit speed, the two entities are equal, because each is a unit displacement from unit speed, albeit in opposite “directions.” This equality works out beautifully for identifying the various entities of the standard model as combinations of preons, but not so much for the energy properties of the wheel of motion.
In the latter case, the number four, the quotient relation of the relative number of S|T units in the preons appears to be more important, because we are dealing with the relative energies of the SUDRs and TUDRs in our investigation of the atomic spectra.
But now that we have the quantitative number four (i.e. T|S = (2/1)/(1/2) = 4) , what we need is to understand the n2 part of the equation. What physical property corresponds to the n and why is it squared? We have sought an answer to this question in the mathematics and geometry of the LC and tetraktys for years, but have only been teased with intriguing hints.
In the quantum mechanics of the LST, the n in their 2n2 equation corresponds to the energy shells of the nuclear atom, and the shells host the orbits of the two electrons allowed by the Pauli Exclusion principle in each orbit, which all fits so nicely into the classical idea of angular and orbital momentum and the four quantum numbers of QM. However, truth be known, you can’t look too closely, or some serious flaws appear in the model.
In the RST based model we are building, consisting of combinations of 3D space oscillations (SUDRs) and 3D time oscillations (TUDRs), the number of electrons is associated with the number of protons, but the electrons are not modeled as residing in concentric shells orbiting a nucleus, but oscillating in connection with the associated proton, which, again, leaves us with the question, “If the n term in the 4n2 periods of the wheel does not correspond to shells, as does the principle quantum number, N, of the QM atomic model, what does it correspond to?”
Whatever the answer is, it has to have a square relation, not a cubic one, which is puzzling given that the the volumes of the atoms would seem to determine their order, not their cross sections. Yet, the 22, 42, 62, 82 of the periods correspond to the increasing areas of the expanding LC, not the increasing volumes.
Well now it appears that the square relation might reside in the relation of the inverses, at least at the unit level. To see this, we merely need to recognize that the inverse of the tetraktys is the double of the binomial, just as the inverse of the LC is it’s double. Remember, this follows from the equation of inversive geometry, where
r’2 = r * r”
When r is 1, then r’ is the square root of 2 and r” is 2, which is the next set of right lines in the expanding LC. In other words, the 2x2x2 stack of 8 unit cubes expands to a 4x4x4 stack of 64 unit cubes in the discrete expansion of two units of time, which just contains the continuous outer circle expansion of the LC. So, if we relate a 2D slice of the LC to the number line, the nested right lines and circles correspond to the numbers on the 0D time line (radii of the circles), the 1D diameters, the 2D areas and the corresponding 3D volumes (that are implied from the 2D slice.)
However, recall that we found that the number 1, the radius of the inner ball of the LC, is troublesome, since 1n is always equal to 1, regardless of the magnitude of n, so our new number line drops down one level, so-to-speak, to the next smaller ball, with radius r equal to the inverse of the square root of two, which is the inverse of the radius of its associated outer ball, with radius equal to the square root of 2. This is shown in figure 1 below.

Figure 1. The Right Lines and Circles of Larson’s Cube Fitted to the New Number Line
The relation of inversive geometry is still the same, but now r = 1/(21/2) (green radius), r’ = 1 (red radius) and r” = 21/2 (blue radius) and the equation, r’2 = r * r” still holds true: 12 = 1/21/2 * 21/2.
Generating a new unit LC on this basis gives us a tetraktys of
1. 20 * (1/21/2) = 1/21/2
2. 21 * (1/21/2) = 21/2
3. 22 * (1/21/2) = 81/2
4. 23 * (1/21/2) = 321/2
Therefore, instead of the corresponding inverse tetraktys being doubled to a quadnomial expansion, 40 = 1, 41 = 4, 42 = 16, 43 = 64, it is doubled to the square root of 2, since 2 * (1/21/2) = 21/2, giving us:
1. 20 * (21/2) = 21/2
2. 21 * (21/2) = 81/2
3. 22 * (21/2) = 321/2
4. 23 * (21/2) = 1281/2
for the inverse tetraktys.
Hence, whereas the ratio of the unit expansion of the tetraktys to the unit expansion of its inverse tetraktys, at each level of the tetraktys, using the unit of the traditional number line, is,
- 20:40 = 1:1 = 1:1 (point to point ratio (duration ratio))
- 21:41 = 2:22 = 1:2 (line to line ratio)
- 22:42 = 4:42 = 1:4 (area to area ratio)
- 23:43 = 8:82 = 1:8 (volume to volume ratio),
now, the ratio of the expansion of the tetraktys to the expansion of its inverse, which corresponds to the unit of the new number line, is a constant ratio, 1:2, at all four levels:
- 1/21/2:21/2 = 1:2 (point to point ratio (duration ratio))
- 21/2:81/2 = 1:2 (line to line ratio)
- 81/2:321/2 = 1:2 (area to area ratio)
- 321/2:1281/2 = 1:2 (volume to volume ratio)
This is very interesting, using the new number line like this, because, since the TUDR tetraktys is the inverse of the SUDR tetraktys, their product is 1/2, at each level, while the inverse of this ratio is, of course 2/1.
Could it be that we are on to something here? More later.
Update: I don’t know why I wrote “product” in that last statement, when it obviously should read “quotient.” However, the product too is interesting, since it gives us:
- S0 * T0 = 12
- S1 * T1 = 22
- S2 * T2 = 42
- S3 * T3 = 82
Notice that the exponents of these factors are not summed in the product, because they indicate the geometric dimensions of S and T, not the number of factors in a number. The number of factors is contained in the tetraktys itself, but when we multiply these by the unit, 1/21/2, or the inverse unit, 21/2, it’s as if we are counting these as the sides of the square (4), and the edges of the cube (8).
The exception is the 0D components, because they are mathematical inverses, while the others are not. None of this may matter in the final analysis, since the product of space and time normally doesn’t make sense conceptually.
In the next post, we will discuss the analog magnitudes of the tetraktys and LC.
The Philosophy of Mathematics, Geometry and Physics
One of the things that the FQXI contest highlights is just how much mathematics, geometry and physics enter into philosophical discussions! There is no way to get a handle on anything other than a small fraction of the discussions the contest generates, and the mix of professionals, semi-professionals and amateurs makes for a unique and stimulating experience. I encourage all ISUS members and interested non-members to participate.
I mentioned one of the effects the contest has had on me in the New Physics blog: It forced me to recognize that the number line is sensitive to perspective. With respect to the unit progression, or the physical datum of the physical system, the RST, there is only a difference in “direction” between less than unity and greater than unity speeds, while from the perspective of one or the other, the inverse is alway greater.
In other words, from the perspective of 0 (i.e. 0 displacement from unity), a unit space/time displacement of 1/2 is no different than a unit time/space displacement of 2/1, except in “direction.” They are separated by two units, one in one “direction” and the other in the opposite “direction.” However, from the perspective of 1/2, 2/1 is four times as great, or it is one-fourth as big. On the other hand, from the perspective of 2/1, the same perception holds. An observer in the t/s sector of the universe would regard his time (our space) and his space (our time) exactly the same way we do.
But, from the perspective of a unit speed, a slower speed than unit speed is not the same as a higher speed than unit speed, just as .5 is not the same as 2, though they both are one unit of displacement removed from unity, in opposite “directions.” There is a quantitative difference as well as a qualitative difference, in the latter case.
Hence, in considering the mathematics of the new number line, there are these two aspects of the same relationship to wrestle with. How do we add, subtract, multiply and divide with these 3D numbers? If we add two s/t units, is the sum greater or less than one t/s unit? If less, then four s/t units are equivalent to one t/s unit. If greater, then one s/t unit is equivalent to one t/s unit. Since the universe of motion deals with speeds, I have always thought that the unequal relation held, but when I realized that the 3D inverse of space is required for 3D oscillation, then the equal relation is required.
This leads me to think harder about rational numbers. When a rational number is equated with the infinite parts of a whole, a fraction of the whole, then these fractions and multiples of the whole reside entirely within the realm of positive real numbers: 0 —> infinity. But when a rational number is equated with two, reciprocal, aspects of one component, such as two orthogonal dimensions of space, then both magnitudes are multiples of the whole, residing entirely within the realm of 0 —> infinity, because they are completely independent variables.
Of course, we can add fractions of the whole to the accumulated total of units, in each orthogonal dimension, in order to obtain greater precision in specifying these positive magnitudes of space, but we can clearly see that the meaning of the rational number, as a fraction of a positive magnitude, and its meaning as the ratio of the magnitudes of the two orthogonal dimensions, are quite distinct.
In the context of the space/time ratios, where space is taken to be the inverse of time, we need to make the same type of distinction between the two meanings of rational number. Larson’s conclusion was that the discrete unit postulate prevents fractions of units, in all but the effective sense. In other words, when the limit of a discrete unit is reached in the relations between motions, then motion, s/t, limited by the discrete unit of space, can revert to motion, t/s, which is to say, motion in time, something Larson called “equivalent space.” He writes in “New Light on Space and Time”:
Let us consider an atom A in motion toward another atom B through free space…. According to accepted ideas, atom A will continue to move in the direction AB until the atoms, or the force fields surrounding them, if such fields exist, are in contact. The postulates of the Reciprocal System specify, however, that space exists only in units, hence when atom A reaches point x, one unit of space distant from B. it cannot move any closer to B in space. It is, however, free to change its position in time relative to the time location occupied by atom B. The reciprocal relation between space and time makes an increase in time separation equivalent to a decrease in space separation, and while atom A cannot move any closer to atom B in space, it can move to the equivalent of a spatial position that is closer to B by moving outward in coordinate time. When the time separation between the two atoms has increased to n units, space remaining unchanged, the equivalent space separation, the quantity that will be determined by the usual methods of measurement, is then 1/n units. In this way the measured distance, area, or volume may be a fraction of a natural unit, even though the actual one, two, or three-dimensional space cannot be less than one unit in any case.
This is an astounding, but perfectly consistent concept. It means that the only way a unit radius ball of space can contract to zero is for an inverse ball of time to increase to unit radius and vice-versa, but Larson never envisions this idea of equivalent space (time) in any other sense than that of relative positions, the non-progressing locations of space and time occupied by atoms. Clearly, however, the consequences of this concept ought to manifest themselves much earlier in the development of his RSt. The reason they don’t, I suspect, is that Larson’s initial progression reversals are 1D not 3D, as are ours, and the requirement for the contraction of 1D units to zero, needing to be accompanied by the expansion of 1D units of the reciprocal aspect, is not as apparent in the 1D case as it is in the 3D case.
Regardless, the idea that 3D time, or 1/s3, must increase from 0 to 1, if 3D space, or s3/1, is to decrease from 1 to 0, is a fundamental consequence of the RST postulates. The fact that it is mathematically consistent is shown by the 2D analogy of rotation, when we describe rotation by the changing angle of the radius, together with the changing angle of its inverse, or the two changing angles of the rotating diameter of the unit circle. As one end of the diameter rotates the last degree, say inward from 179 degrees toward 180 degrees (or 1), the inverse end MUST rotate inward from 359 toward 360 degrees (or 0), and as the rotation of the diameter reverses “direction” at 180 degrees, heading away from 180 degrees outward toward 181 degrees, the inverse end must also reverse “direction” heading outward from 360 degrees (0) toward 1 degree. There is no other way.
So this is a major distinction between the rational numbers of true inverses, and the rational numbers of orthogonal variables. In the latter case, we can change the magnitude of one, without affecting the other, but not so in the case of the former. At least in the case of the space/time progression, where it serves as the datum of the physical universe, an increase in space has the same affect on the magnitude of the motion, as an increase in time, just as the magnitude of an area is affected equally, regardless of which of its two, orthogonal, dimensions is increased or decreased.
The difference is that the magnitude of an area is not normally required to be held constant, while the magnitude of the natural progression of the RST is. Therefore, we cannot always treat the numbers in the space/time ratios that pertain to the order of progression, in the same manner that we treat the numbers of the x/y dimensions that pertain to bounded magnitudes.
For instance, we cannot just add (subtract) quantities of space (s/1), or quantities of time (t/1), to/from existing units of motion, changing their magnitudes. In order to change the magnitude of motion (s/t or t/s), we have to add (subtract) units of motion to/from units of motion.
So this difference requires a different algebra than the one we use with the notion of bounded magnitudes. It is an algebra restricted to rational numbers, where the two units that form the numbers of the number system that constitute the unit ratio cannot be sub-divided, as with a knife. The range of sub-divisions of the bounded magnitudes of traditional algebra is unlimited, but no such concept is possible in the new algebra.
This has many consequences, some of which we will try to explore here soon.
The New Scalar Number Line
As we’ve seen, the new scalar math requires a new scalar number line. The familiar number line, though simple and straightforward, is philosophically troublesome due to the enigmatic status of zero and negative numbers. Even so, it has been used to define integers and rational numbers, using a concept of 0 as a sort of number and -1 as the foundation of a set of multi-dimensional algebras called Lie algebras.
This has worked out fairly well for the research program of physics based on the vectorial motion in the LST, but it is totally unsuitable for the physics based on the scalar motion of the RST. We need a more complex, complete and consistent view of the scalar number line in order to use scalar mathematics in the development of the RST’s scalar theory.
However, the first thing we notice is that the RST’s scalar progression is 3D and therefore non-linear. Fortunately, though, we can use the combination of Larson’s 2x2x2 cube and its associated inner and outer spheres to construct a new, mult-dimensional, scalar number line that is linear. There are several aspects to this approach and, to understand it, we will have to take them one at a time.
The first thing we want to note is that the multi-dimensional magnitudes of the cube are integer indexes to the non-integer multi-dimensional magnitudes of the associated spheres. This is important to understand, since it enables us to unify the integer and non-integer magnitudes the way nature does, and, hopefully, it provides the key to understanding the mysterious connection between mathematics and physics.
To demonstrate what is meant by indexing the continuous magnitudes of physical variables with the discrete variables of numbers, we need to begin by analyzing the dimensions of Larson’s cube, as shown in figure 1 below.

Figure 1. Multi-Dimensional Number Line from Expansion of Larson’s 2x2x2 3D Cube.
In a 3D numerical progression, n3, all three dimensions (four counting 0) - the dimensional resolutes we might say - expand with the cube simultaneously. The magnitude of the 0 dimensional expansion, n(20), increases as a function of one-half of any given axis; the magnitude of the 1 dimensional expansion, 3(2n), increases as a function of the six 1D “directions” of the three axes; the magnitude of the 2 dimensional expansion, 3(2n)2, increases as a function of the 12 2D “directions” of the three axes, and the magnitude of the 3 dimensional expansion, (2n)3, increases as a function of the eight 3D “directions” of the three axes.
Figure 1 shows only one quadrant of the expanding cube, and the inner row/column is labeled with the 0 dimensional numbers, while the corresponding 1D, 2D and 3D numbers are labeled as successive outer layers of the quadrant (the factors of 3 in the 1D and 2D numbers comes from the 3 axes of expansion.)
By selecting just one quadrant of the expanding cube and labeling the magnitudes of all four dimensions in this manner, we get a scalar number line, where the vertical line is independent of the horizontal line, which will eventually allow us to include the reciprocal property that at this point is not apparent. In addition to assuming the presence of the other quadrants in the expansion, the figure does not show the third dimension graphically, but assumes its presence (the z axis with magnitudes in front of and behind the page.)
By accommodating all the magnitudes of the four dimensions this way, we can simplify the required graphics considerably, while maintaining the 3D scalar concept. Next, we can add the non-integer complement magnitudes of the associated inner and outer spheres to figure 1, as shown in figure 2 below.

Figure 2. Multi-Dimensional Number Line from Larson’s Cube with Inner and Outer Spheres
Of course, the magnitude of the radius of the inner sphere is always an integer and that of the outer sphere is always a non-integer, when n >= 1. Multiplying the multi-dimensional values of the outer radii by factors of pi, we obtain 1D (circumference), 2D (surface) and 3D (volume) continuous multi-dimensional magnitudes, indexed by the corresponding integers.
However, while the outer radii are multiples of the square root of 2, when the 0D magnitudes are greater than 1, the inner radii are inverse multiples of the inverse of the square root of 2, when the 0D magnitudes are less than 1, as shown in figures 3 and 4 below.

Figure 3. Outer Radii are Multiples of the Square Root of 2 at Indexes Greater Than 1.

Figure 4. Inner Radii are the Inverse Multiples of the Inverse of the Square Root of 2 at Indexes Less Than 1.
Hence, we can plot the radii linearly on a line, what we are want to call the new scalar number line:
…1/3(1/21/2), 1/2(1/21/2), 1/1(1/21/2), 1/1(2/11/2), 2/1(2/11/2), 3/1(2/11/2)…
comparing this to the traditional scalar number line:
…1/3, 1/2, 1/1, 2/1, 3/1…,
we see several differences. First, there is a distinct difference between the counting multiple and the unit. In the traditional line they are one and the same: 1(1), 2(1), 3(1), …, but in the new line the counting multiple, successive increments of 1, is very different from the unit, which is the square root of 2.
Proceeding in the opposite “direction,” the counting multiple of the traditional line is the inverse of the positive multiple, while the unit is the inverse of 1: …1/3(1/1), 1/2(1/1), 1/1(1/1), but because the inverse of 1/1 is indistinguishable from 1/1, it is not recognized that there are TWO units involved, where one is the inverse of the other.
In the new line, the unit of the outer sphere is the square root of 2, while the unit of the inner sphere is the inverse of the square root of 2, as can be clearly seen by comparing figures 3 and 4, so this requires two instances of the mathematical value of 1, if you will.
Interestingly enough, one of the confusing issues of working with the scalar concepts of the RST, is that while 1/1 is equal to 1/1 mathematically, s/t is not equal to t/s physically. The new scalar number line should be a great help in this regard.
Update: I just noticed that the graphic in figure 4 is the wrong one. I’m making a new graphic for it now and will update the figure soon.
Update: Replaced graphic in figure 4 (please pardon the distortions.)
The New Math
It’s been a long time since my last entry on this blog. Mostly that’s due to time constraints, but also because I’ve written about things on the new physics blog that probably should have gone here. Sometimes, though, it’s hard to separate the math from the physics topics.
However, there’s no doubt where this topic goes. I want to take the new math from the top, and lay out the new concepts from the beginning. I will be referring to them as I develop the physics theory on the other blog.
The first concept that must be clearly understood from the start is that the reason for calling it the new math is that there are two interpretations of number. the first interpretation of number is the usual quantitative one that is a measure of how much or how many of something there is. In the second, the operational number represents a relation between two quantities.
We begin by viewing the familiar quantitative number line below in light of these two interpretations of number.
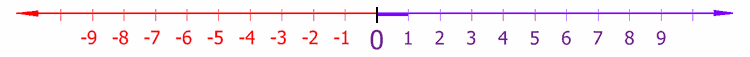
Figure 1. The Quantitative Interpretation of Number Line
In the quantitative interpretation of number, the whole numbers and proper fraction, rational, numbers lie to the right of 0 on the number line, in all cases. For instance, the number 1 occupies the first place to the right from 0, and 1/2 lies half way between 0 and 1 on the quantitative number line. The negative numbers and negative proper fractions to the left of 0 are somewhat problematic and were only accepted by mathematicians gradually and grudgingly. Wikipedia defines them as follows:
Negative integers can be regarded as an extension of the natural numbers, such that the expression x – y has a well-defined value for all values of x and y. Other number systems, such as the rational numbers, are then derived as progressively more elaborate extensions and generalizations from the integers.
On the other hand, in an operational interpretation of a rational number, we can take the relation of the numerator and denominator, say the difference between them, instead of the quotient, and it permits us to replace all the positive numbers on the number line with the reciprocal of proper fractions that replace all the negative numbers on the line, none of which are less than 1.
This way, we get a new number line,
1/n, …1/3, 1/2, 1/1, 2/1, 3/1, …n/1,
which is an operational equivalent of the quantitative number line in figure 1, above, but which is not based on integers, but constitutes a new generalization from which integers themselves are derived. In this case, however, instead of positive and negative numbers, we have a rational number and its inverse. To be sure, while the rational numbers are not the same as the quantitative numbers on the quantitative number line, their operational interpretation is; That is,
1/n = 1-n; …1/3 = -2; 1/2 = -1; 1/1 = 0; 2/1 = 1, 3/1 = 2, …n/1 = n-1;
In Larson’s new system of physical theory (RST), as opposed to the legacy system of physical theory (LST), there are two, reciprocal, sectors of the physical universe, the sector where motion is above unity (the cosmic sector), and the sector where motion is below unity (the material sector.) Within each of these two sectors, there is an important sub-sector, the interior of unit distance, which Larson refers to as the time region (inside unit space) and the space region (inside unit time).
A complete mathematical analogy of this space-time structure can be reproduced by considering the quantitative and operational interpretations of number together. The operational interpretation extends outward from 0 (1/1) to infinity, in both “directions,” while the quantitative interpretation extends inward from 1 and -1 (i.e. 2/1 and 1/2 respectively) to 0 (i.e. 1/1), in both “directions.”
However, there is another important distinction between these two interpretations of number, besides their respective data of 0 and 1, and it must be understood as well. In the operational interpretation, we must pick a perspective; that is, we must view the reciprocal side of the datum from its inverse perspective, just as we must view a see-saw from one side or the other. We cannot view the operational interpretated number line from both sides at the same time, any more than we can view the see-saw profile from both sides of the fulcrum at the same time. In terms of motion, this means we must choose to interpret both views as above and below unit motion, or above and below unit inverse-motion (s/t or t/s, but not both together.)
On the other hand, in the quantitative interpretation of number, we must view the reciprocal side of the datum from its own perspective, where one side is motion, while the other side is inverse-motion (s/t and t/s, at the same time.) This difference is illustrated in figure 2 below.

Figure 2. Operationally and Quantitatively Interpreted Number Lines
The division operation of the quantitative (how much or how many) interpretation of number requires us to differentiate the positive and negative quantities, as if they were real, even though there is no such thing as a negative quantity. As Sir Rowland Hamilton observed:
it requires no peculiar scepticism to doubt, or even to disbelieve, the doctrine of Negatives
and Imaginaries, when set forth (as it has commonly been) with principles like these: that a
greater magnitude may be subtracted from a less, and that the remainder is less than nothing; that two negative numbers, or numbers denoting magnitudes each less than nothing, may be multiplied the one by the other, and that the product will be a positive number, or a number denoting a magnitude greater than nothing; and that although the square of a number, or the product obtained by multiplying that number by itself, is therefore always positive, whether the number be positive or negative, yet that numbers, called imaginary, can be found or conceived or determined, and operated on by all the rules of positive and negative numbers, as if they were subject to those rules, although they have negative squares, and must therefore be supposed to be themselves neither positive nor negative, nor yet null numbers, so that the magnitudes which they are supposed to denote can neither be greater than nothing, nor less than nothing, nor even equal to nothing.
Contemplating the arbitrary nature of the quantitative number line, Hamilton sought a better approach using the dynamic concept of order in progression, rather than the static concept of bounded magnitude. This was a good idea, as far as it went, but it requires two orders of progression to make it work, not just one. Hamilton’s idea was to use the flow of time to give algebra an intuitional foundation, but Larson’s idea was to use the flow of time, together with the flow of space, to put physics on an intuitional foundation.
At first Larson’s idea seems absurd, and it would never had ocurred to Hamilton, but today the flow of space has actually been observed. The logical conclusion is that the two should be considered together. The difficulty is recognizing that they are not separate quantities, but actually two aspects of the same quantity, motion. We start with unit motion and go in both “directions,” toward greater or less than unit motion, when the flow of one aspect is less than the flow of the other.
Larson’s conclusion was that the only possiblility of introducing a difference between the two flows, is to assume that one or the other of them periodically reverses its “direction.” He called this simple harmonic motion, and he pointed out that it was just as reasonable to believe that the flow of space, or of time, could oscillate as not, and that this is the basis of all physics.
Were this the summum and bonum of the subject, we would be home free, but it is not complete at this point, because the two inverse aspects of the universal motion, the two flowing quantities, if you will, do not have the same dimensions. The flow of space exists in three dimensions, while the flow of time has no dimensions. Mathematically, then, the natural progression is not linear. If:
s/t = 23/20
then it does not give us a natural progression of 0, 1, 2, 3, … but rather it gives us a progresssion of 0, 8, 216, 512, …, and, at first glance, it’s totally impractical to construct a number line from such a non-linear progression.
However, it turns out that, within this 3D progression, there is an associated 0D, 1D and 2D progression as well, and by recognizing that the natural progression contains all four numerical progressions, we can construct a new, composite, number line and with it a new number system to use in our investigations of the RST. We will take a look at it next time.