The New Mathematics
Toward Non-pathological Algebras
Arguably, the two most challenging mathematical/philosophical problems for the Greeks were manifest in the attempt to square the circle and to accept the existence of irrational numbers. In modern times, we’ve proven that the former is impossible, and the latter is actually quite useful. However, as discussed in the previous post, it is possible that there are other approaches to meeting these formidable challenges, unknown to us, which might even prove more useful than our current method of handling them.
The crucial analysis of the fundamentals that seems to provide us with the clues that this might be so starts with Larson’s idea of scalar motion. As regular visitors of the LRC site know, scalar motion is a definition of motion without reference to moving objects. The equation of motion, v =ds/dt, simply involves a change in space over time, and a changing location of an object is not required to produce the equation’s change of space, just as it is not required to produce its change of time.
In Larson’s system, the initial condition of the universe assumes a natural space clock as well as a natural time clock, the one being the inverse, or reciprocal, of the other. Hence, this assumption defines a universal motion, as the physical datum of the system. There are several important differences between the new natural type of motion, with no motion of an object involved, and the motion of objects with which we are familiar. One of the most basic differences is that the familiar motion of an object Y, from point X to point Z, increases the distance XY and decreases the distance YZ. On the other hand, the new natural type of motion changes distance itself; that is, both the distance XY and YZ are increased, or decreased, at the same time, making it impossible to define the motion of the object Y, in terms of the changing distance relative to X and Z, with one increasing and the other decreasing. It’s as if the size scale of the system were changing.
This expansion/contraction motion, though easily observed in nature, is quite unlike the motion of an object from one point to another, specified in some specific direction that can be defined in terms of three dimensions. In a 3D system, scalar motion would change the size of a spatial location in all three dimensions simultaneously. This makes scalar motion more difficult to work with in some respects, because the system’s locations (x, y, z), regardless of size, must continuously expand. While at first this is very disconcerting, it turns out that there are ways to cope with it that are straightforward.
Consider a 1D scalar expansion for instance, disregarding the expansion of the points themselves momentarily, the distance between points A and B increases over time. We can choose location A as a reference and measure the expansion in terms of B’s motion away from A, or we can choose B as the reference and measure the expansion in terms of A’s motion away from B, in the opposite direction. Either way, we can conclude that each dimension of scalar motion has two, opposed, directions. In a 1D system there are two scalar directions, in a 2D system there are four scalar directions, and in a 3D system there are eight scalar directions.
Assigning numbers to the binary directions in each dimension, we get 20 = 1 direction, in the zero-dimensional system (more on this exception below), 21 = 2 directions, in the one-dimensional system, 22 = 4 directions, in the two-dimensional system, and 23 = 8 directions, in the three-dimensional system. Substituting these numbers in the equation of motion, we would get:
ds/dt = d20/d20, for zero-dimensional motion,
ds/dt = d21/d21, for one-dimensional motion,
ds/dt = d22/d22, for two-dimensional motion,
ds/dt = d23/d23, for three-dimensional motion,
However, as we observe time, it’s clear that it has only one direction, called the “arrow of time,” which is increasing magnitude only; that is, a point in time has no direction, and therefore no extent, in space. On this basis, we can consider time as a zero-dimensional scalar, something that can be counted, but not expanded. Meanwhile, it’s clear that the space that we occupy is three-dimensional; that is, it extends into three dimensions, and, since scalar motion has no specifiable direction, by definition (i.e. it is motion with magnitude only), the expansion of space must be effective in all of the dimensions of the system (i.e. space is a pseudoscalar). Modifying the equation of scalar motion accordingly, we get
ds/dt = d23/d20,
where space, s, has 23 = 8 directions, and time, t, has 20 = 1 direction, the scalar “direction” of increasing magnitude only. By defining space and time this way, as the reciprocals of each other, in the equation of motion, the quantity space is differentiated from the quantity distance, which becomes the product of motion and time, as in the ordinary vectorial motion (i.e. motion with direction defined by locations with three dimensions). However, in this case, using the scalar motion equation, distance, d, is a three-dimensional quantity, not a one-dimensional quantity:
d = Δs3/Δt0 * t0
= (n2)3/(n20) * n20
= (8*13)/(1*1)
= 8*13
for each unit of change, n. For example, for two n, we get
d = ((2*2)3/(2*20) * (2*20) = (64*13/2) * 2 = 64*13,
or 64 cubic units of volume expansion in two units of time. The expansion series, or “distance” d, as time, t, marches on then is not the familiar linear series of lengths 11, 21, 31, 41, …n1, but the less familiar, non-linear, series of volumes, 83, 643, 2163, 5123, …n3.
Geometrically, the first term in this expansion series corresponds to the initial 2x2x2 stack of one-unit cubes, dubbed Larson’s Cube, at the LRC. It is shown in figure 1 below.
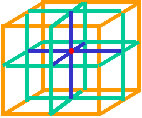
Figure 1. Larson’s Cube as the 8 Unit Stack of One-Unit Cubes.
The red dot in the center corresponds to the 20 = 1, dimensionless, time magnitude, while the stack of eight 3D cubes corresponds to the 23 = 8 * 13 space magnitudes, at t1 - t0 = 1. Expanding in the next unit of time, at t2 - t0 = 2, to two units of space in all directions, it’s easy to see that the stack of one unit cubes, consisting of of 2x2x2 = 8, one-unit, cubes, in figure 1, expands to a 4x4x4 = 64 stack of one-unit cubes. In the third unit of time, the stack expands to a 6x6x6 = 216 units, then to a 8x8x8 = 512 units, and so on, ad infinitum. Meanwhile, the 20 point at the intersection of the cubes, does not expand.
However, this mathematical expansion of the pseudoscalar does not correspond to a physical expansion, because a physical expansion of the pseudoscalar must expand in all directions, defined by three dimensions, not just the three orthogonal directions that constitute its three dimensions. Thus, the physical expansion is manifested as an expanding sphere, not as an expanding cube, and this presents us with the fundamental challenge faced by the Greeks: “How do we calculate the volume of the sphere that corresponds to the volume of the stack of one-unit cubes?” In other words, we need a geometric algebra of quantities that includes the areas of circles and the volume of spheres, as well as the linear extent of right lines, an algebra, which corresponds to a fully functional, non-pathological, numeric algebra, for doing physical calculations in a scalar/pseudoscalar system. In other words, it’s back to the old conundrum of squaring the circle.
Unlike the Greeks, however, we now know that multiplying the sides of a polygon inside the sphere will always result in an approximation, and thus it can’t be represented by a rational number. Since in our universe of discrete motion, as in the Pythagorean universe of discrete numbers, all is number, this is hardly welcome news.
Nevertheless, as we consider the problem, we see that there are two spheres that can be related to the stack of one-unit cubes. One sphere that can be drawn to fit just inside the stack, and the other that can be drawn to just contain the stack. A two-dimensional view of the one-unit instance of these three figures is shown below.
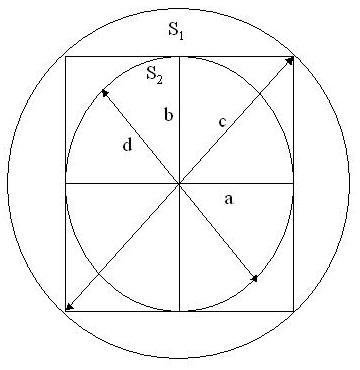
Figure 2. Two-Dimensional View of 2x2x2 Stack of One-Unit Cubes with Inner and Outer Spheres
In figure 2, the radius, c, of the outer sphere, S1, is the square root of 2, by the Pythagorean theorem, while the radius, d, of the inner sphere, S2, is 1, since the radius is r = a = b = 1. By the formula for the area of the surface of a sphere,
A = 4π * r2,
the area of the surface of the sphere S1 is 8π, while the area of the surface of the sphere S2 is 4π. Also, by the formula for the volume of a sphere,
V = 4/3π * r3,
the volume of the sphere S1 is the square root of 2, cubed, times the volume of S2, which is just 4/3π, since its radius is 1.
Table 1 shows the tabulated circumferences (2*r*π), areas and volumes for spheres S1 and S2, and their ratios, for units 1, 2, 3 and 4.
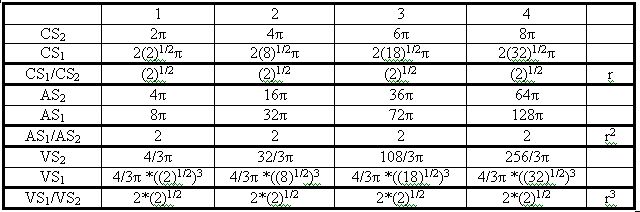
Table 1. Circumferences, Areas and Volumes for Units, 1, 2, 3 and 4
Notice that the S1/S2 ratio is just a power of the radius of S1, or a power of the square root of 2, in each case, denoted “rn” in the last column of the table. The ratio of the surface areas of the spheres is the square of r, or 2, while the ratio of the volumes of the spheres is twice the radius of S1, which is equivalent to the square root of 2, or r, cubed.
This is an amazing fact that we should be able to exploit in order to replace the 20, 21, 22, 23, numerical units that are so hard to reconcile in a non-pathological, multi-dimensional, algebra.
Recall that, currently, for one-dimensional units, we resort to complex numbers (z = a+bi), the algebra of which is not ordered; For two-dimensional units, we resort to quaternions, the algebra of which is not ordered or commutative, and, for three-dimensional units, we resort to octonions, the algebra of which is not ordered, commutative, or associative!
All of these traditional units depend on one or more imaginary numbers to define their dimensionality, arbitrarily defined as the square root of -1, in the different dimensions of the respective algebras. Of course, in reality, there is no unit that can be physically identified that, when multiplied by itself, is equal to -1, in any dimension.
However, we should remember that the purpose of using the plus and minus signs is only to differentiate between a given dimension’s two “directions.” There’s nothing meaningful about them otherwise. As already noted above, in scalar motion, the choice of a fixed reference (point A or B), with which to measure scalar change, is completely arbitrary.
The same thing is true with numbers. Each number has its inverse and the designation as to which is the number and which is the inverse number is completely arbitrary. Nevertheless, with the number 1, we say that it is its own inverse, and we use this convention to build group theory, where 1 is the identity element.
However, if we could change our number system, from one based on multi-dimensional numbers, using imaginary numbers to define their dimensions, and plus and minus labels to define the two directions of each of their dimensions, to one based on the properties of spheres (i.e. 1D circumferences, 2D surfaces and 3D volumes), the inverse of 1 would no longer have to be itself, but would now be 2, the inverse of 2 would be 4, etc, by the formula for inverse geometry, r’2 = r * r’’.
In this way, negative numbers are eliminated conceptually, although the change is actually only one of perspective. It’s like saying that the inverse of -1 is 2 units above it; the inverse of -2 is 4 units above it; the inverse of -3 is 6 units above it, etc. In this case, however, the unit referred to is the square root of 2, r, which is not imaginary, but is the relation between unit dimensions, defining the radius of a sphere.
Just like in the traditional mathematics, the new unit, r, defines the identity element of a group. Figure 3 shows the number 1 of the group, P, the group identity element, P’ (equal to the square root of 2), and the inverse of number 1, p’’ (equal to P’ squared, or 2).
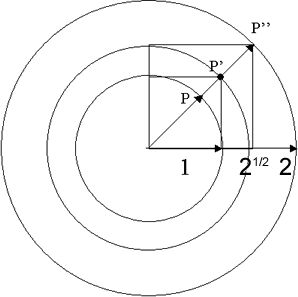
Figure 3. The number 1 of the group (P), the identity element (P’), and the inverse of number 1 (P’’).
In figure 3, P is the radius (1) of the inner sphere, the generator of one 1d (circumference) quantity, one 2d (surface) quantity and one 3d (volume) quantity. Radius P’ generates the 1d, 2d and 3d quantities of the identity element (square root of 2), while P” is the radius (2), or the inverse of radius P (by P’2 = P * P’’), the generator of its 1d, 2d and 3d quantities.
This is no different than the number line, where -1 is one unit removed from 0 and two units removed from +1. The difference is huge, though, because we can represent all three of the dimensional numbers with one radius, and do away for the need of imaginary numbers (C = circumference; A = area; V = volume for the given dimension’s P, P’ and P” quantities):
1) 1D: CSp = 2π (i.e. -1); CSp’ = 2π*r (i.e. 0); CSp” = 4π (i.e. +1)
2) 2D: ASp = 4π (i.e. -12); ASp’ = 4π*r2 (i.e. 0); ASp” = 16π (i.e. +12)
3) 3D: VSp = (4/3)π (i.e. -13); VSp’ = (4/3) π*r3 (i.e. 0); VSp” = (32/3)π (i.e. +13)
The fact that each successive dimension has it’s own “zero” quantity, or identity element, might take some getting used to, but it would be well worth it, if it enables us to get rid of imaginary numbers and the pathology of higher-dimensional algebras.
In that case, we would have an algebra of 0D scalars, an algebra of 1D pseudoscalars, an algebra of 2D pseudoscalars, and an algebra of 3D pseudoscalars, each one with all three algebraic properties of order, commutativity and associativity.
We’ll see.
Fundamental Consequences
There’s a tendency in our society to understand the history of human thought as a more or less linear progression from primitive to sophisticated. As we think of Western civilization’s technological progress, from horse and buggy, to manned space flight, it’s easy to view our revolutionary capabilities in science and technology as the pinnacle of human achievement, and to suppose that there is no other way forward, but along the way we have traveled.
However, the ancient Hebrews envisioned our days and characterized them, not as the pinnacle of civilization’s progress, but rather as the deterioration of civilization’s worth, inferior to the quality of previous civilizations. The image of the relatively inferior status of modern nations was explained by the Hebrew Daniel, when he saw and interpreted the king of Babylon’s dream, portraying the progressive degradation of the quality of earth’s civilizations, from that time to this.
According to this vision, the ancient Babylonian kingdom was the highest quality civilization in the world, followed by the inferior, but stronger, Persians, who were followed by the still more inferior, but stronger, Greeks, then by the vastly more inferior and stronger Romans, and finally by the remnants of the Romans, mixed in with the conquering Barbarians, the most inferior, totally fragmented, uncivilized nations of all, who were as clay mixed in with the metal of the Romans. The Romans were as iron compared to the more highly prized bronze of the Greeks and to the sliver of the Persians and to the gold of the Babylonians.
Of course, in the end, all of this is irrelevant, as the vision portrayed all of these old kingdoms as being replaced by a new Hebrew kingdom, which would come rolling forth like a stone down a mountain, smashing the image of Western civilization’s heritage, in all these old kingdoms, to dust. Consequently, the dust of the pulverized image simply blows away, like chaff in the wind, and disappears!
But what does this have to do with modern mathematics and science? We don’t know much about the mathematics and science of the Persians and Babylonians, and what we do know comes to us primarily from the Greeks, who learned from the Babylonians, the Persians, and the Egyptians (who, like the Asians, were never a world dominating nation, but nevertheless were sometimes significant players in mathematics and science).
Clearly, however, the strength of the Persians, relative to the Babylonians, and the Greeks, relative to the Persians, and the Romans, relative to the Greeks, and, in general, the modern nations relative to the ancient ones, is based, in part at least, on the progress of technology. Whether it is based on advanced strategic technology, such as provides greater sustenance, infrastructure and internal strength for the nation as a whole, or on advanced tactical technology, providing for improved weapons, communications and mobility to the nation’s armies, navies, and air forces, technology has always played a crucial role in the strength of civilizations.
The interesting aspect of this in the present context is that, while it shows us how understanding the simple fundamentals of mathematics and science makes a profound difference in the power and technological capabilities of nations, it also shows us that there may be nothing particularly enduring about it either. Civilizations come and go, and the particular aspect of their understanding of math and science that made them capable of great feats of organization, engineering and technological exploitation, comes and goes with them.
From the smallest of means, proceeds that which is great, the ancients said. For example, who could have guessed that the ability of a few Renaissance scientists to deal with the esoteric concepts of irrational and negative numbers would eventually lead to the modern ability to transcend the technology of the ancients so dramatically? But so it is. Without the ability to abstract the square root of 2 and -1, the whole of modern technology would be impossible.
However, knowing this, we are soon lead to ask what other, simple, fundamentals might we be missing? The fundamentals that some future civilization (perhaps the triumphant kingdom of the Hebrews foreseen by Daniel) might discover, might enable them to transcend our technology as much as we have transcended that of the ancients (or even more).
In thinking about this, one might be tempted to revisit the whole notion of irrational and imaginary numbers, the foundation of modern technology, and seek to understand what it is about this whole approach that makes it so powerful. If there is one way to do this, might there be another, maybe even better way to do it?
Of course, readers of these blogs know that here at the LRC we believe there is, and that we are taking our clues on how to proceed from the works of Hamilton, Grassmann, Clifford, Hestenes, and Larson. Hamilton showed us how defining numbers, as traditionally taken for granted, leaves algebra without a suitable scientific basis. Grassmann showed us that there is an underlying connection between geometry and algebra that the Greeks couldn’t make, and Clifford showed us how the two directions of each dimension forms an algebra. Thanks to the work of Hestenes, which brought the works of Grassmann and Clifford to light, we are provided with tremendous insight into the underlying nature of complex and quaternion numbers, and the imaginary numbers that they are built with.
Finally, none of it would have even caught our attention had it not been for the transcendent work of Larson. It is his brilliant recognition and intriguing development of the new and unfamiliar notions of scalar motion that provides us with the motivation for digging into all these ancient mysteries, driving us to uncover the old foundations, in search of new insight into what makes modern math and physics tick.
What we have found astounds us. Could it be that, as Thales and Pythagoras apparently learned from their predecessors, “Everything is number,” after all? The fact that this faith seemed horribly contradicted by the theorem of triangular squares, that squaring the circle could only be approximated, and that the hare could never catch up with the tortoise, and that today, after centuries of effort, we can now name irrational numbers, use them in the calculus to send robots to explore particular parcels of Martian terrain, use computers to calculate π out to a gazillion decimal places, and work with infinite sets, as easily as the Greeks worked with integers, appears to make the whole issue moot.
“Who cares, if the Greeks thought all was number,” one might think. “Our technology, our math and our science reach so far beyond anything ever dreamed of by the Greeks, that it’s patently clear that we have overcome their intellectual obstacles. Let’s just move on.” Ironically, however, that’s just what we can’t do, and the reason that we can’t do it is that the essence of these very same obstacles stands in our way. We now know that nature is both discrete, definitely measured, like numbers, and, at the same time, continuous, infinitely divisible, like distance.
Yet, in spite of the vaunted “work arounds” of our modern mathematics, which have served us so magnificently, irrational, transcendental, and imaginary numbers, finite and infinite sets, etc, we still cannot do as nature does and seamlessly combine the continuous with the discrete. It is frustrating in the extreme. It appears that, if the ancients taught Thales and Pythagoras that all was number, then they were probably just hopelessly naive and the Greeks were simply beguiled by their priestly robes and their high social status. If we can’t do it today, surely the ancient Babylonians and Persians couldn’t do it either.
That may be so, but it doesn’t mean that they didn’t have a valuable insight into numbers and geometry, which has since been lost, one that might prove to be the key to doing what we so desperately want to do. For instance, even though their approximation of π might have been very rough, compared to our very refined approximation, how do we know that it doesn’t matter, in the end? Of course, barring some unexpected archeological find, we are not likely to ever know more about how the ancients thought than the ancient Greeks did, who were in direct contact with them. The point is not, however, that the ancients had the answers we seek. They probably didn’t, but they may have thought about the fundamentals in a way that hasn’t occurred to us, which could prove to be the key for finding the answers.
As it turns out, there are many intriguing clues that the way the ancients thought about numbers, is close to the new way we are thinking about them here at the LRC. In the next post, we will get into some of the details of this.
Natural Numbers
As discussed in the last post, it seems like the only consistent way to produce the natural numbers is via a natural progression of points; that is, the 0D mathematical series
10, 20, 30 …
must be actually
1*20/20, 2*20/20, 3*20/20, …
because, when, starting with space and time only, there are no “things” to count, which implies that the natural series,
11, 21, 31 …
is mathematically incorrect, as an initial condition in a space|time progression, since
1*21/20, 2*21/20, 3*21/20…,
is a natural progression of double magnitudes (one in each “direction”) not single magnitudes. Therefore, as a space|time progression, the natural 1D mathematical series necessarily begins with 2, not 1, and increases by 2, 1D, magnitudes, not 1:
2*11, 4*11, 6*11…,
while the natural series,
12, 22, 32 …,
is also incorrect, because
1*22/20, 2*22/20, 3*22/20, …
is the natural mathematical progression of area, which begins with 22 = 4, 2D, magnitudes, not 1, or 2, increasing the base of the series by a factor of 2:
4*12, 16*12, 36*12….
Finally, the natural 3D series:
13, 23, 33 …
is also incorrect, as a space|time progression, because it is actually,
1*23/20, 2*23/20, 3*23/20, …,
which is the natural progression of volume, its magnitudes beginning with 23 = 8, 3D, magnitudes, not 1, not 2, not 4, again increasing the base of the previous series by a factor of 2:
8*13, 64*13, 216*13 …
All of this means, among other things, that the algebra of these numbers begins with the pseudoscalar value of an n-dimensional progression (2n), not its scalar value (20); that is, each series begins with the corresponding right side of the tetraktys, not the left side. This is because one line has two directions, and one area has four directions, not two, and it is therefore incorrect to write the progression of 1D magnitudes beginning with the scalar magnitude 1 (20), or to write the progression of area beginning with the 21, or 1D, pseudoscalar magnitude. Likewise, one volume has eight directions, not two, and not four, and therefore the natural volumetric series must begin with eight cubic scalars, not one. To accurately denote this, we need to rewrite the 1D progression as
(1*2)1/(1*2)0, (2*2)1/(2*2)0, (3*2)1/(3*2)0, …,
the 2D progression as
(1*2)2/(1*2)0, (2*2)2/(2*2)0, (3*2)2/(3*2)0, …,
and the 3D progression as
(1*2)3/(1*2)0, (2*2)3/(2*2)0, (3*2)3/(3*2)0, ….
It’s important to recognize that, when the uniform 3D progression is measured from a given point (20 = 1), at tn - t0, the apparent one-dimensional interval characterizes the expanding volume by its 1D radius. However, to calculate the true 1D interval, which is the diameter of the volume, the radius must be doubled; to calculate the true 2D interval, the doubled radius, the diameter, must be squared, and to calculate the 3D interval, it must be cubed:
2*11 = 2r = d,
4*12 = d2,
8*13 = d3
However, this brings us face to face with the age old problem of the quadrature, or of “squaring the circle,” because the 2D space component of the 3D space|time expansion must expand geometrically over time, or circularly, and the 3D component must expand spherically, while the algebraic square and the algebraic cube are necessarily rectilinear, and therefore an issue of 2D and 3D numerical integration, or quadrature, and cubature, as it’s sometimes referred to, arises.
That this problem is related to the foundations of quantum mechanics is indicated, when it’s recognized that only one point on the surface of an expanding circle, or sphere, can be measured at any given time. Special relativity makes it impossible to simultaneously specify tn at any more than one point on the 2D, or 3D, surface of the expansion, because points on these surfaces are always moving apart. Therefore, we are brought back to consider the physical enigma of point/wave duality, and the mathematical dilemma of quadrature, and the logical challenge of unifying the concept of the discrete numbers of algebra with the concept of the smooth functions of geometry.
In the next post, we will discuss how the ancient way of dealing with these fundamental issues turns out to be remarkably congruent with our ideas of the space|time progression; that is, what has been called the “mediato/duplatio” (halving/doubling) method of ancient reckoning, intimately associated with the notion of the tetraktys, turns out to be our “factor of 2,” playing in the space|time progression series, as described above, and we will discuss the correspondence between them next time.
This topic is very interesting as it relates the modern concept of rotation, implemented with complex numbers, to our new concept of 3D expansion, implemented with scalars and pseudoscalars, which is a crucial point to understand, I believe.
LRC Seminar - Scalar Algebra
In the previous posts, we’ve seen how to define the “directions” of natural numbers, by defining number as Hamilton did, as order in progression, instead of increased or diminished magnitude. By taking two of these progression-defined numbers, as the two, reciprocal, aspects of one progression, as Larson did, and by defining two interpretations of these reciprocal numbers, we have been able to establish two groups, one group under addition, analogous to the integers, with an identity element of 0, and one group under multiplication, analogous to the fractions, with an identity element of 1.
In the previous post, we showed how combining the unit magnitudes of the positive and negative “directions” defines a two unit “distance,” or interval, analogous to a spatial distance, with two algebraic “directions,” one negative and one positive:
1|2 + 2|1 = 3|3 = 0
(1|2) = -(2|1)
(2|1) = -(1|2)
However, the fact that the pipe symbol indicates that the reciprocal relation is to be interpreted as the value of the difference (sum of opposite signs) between the numerator and the denominator means that any number n|n can be used as the identity element, and since the quantities in the numerator and denominator are defined in terms of order in progression, rather than as increased, or diminished, quantities, it is necessary to recognize how those quantities differ; that is, how does 1 become 2 and 2 become 3, or 1?
With non-reciprocal numbers defined as magnitudes, 1 becomes 2, when two independent magnitudes are summed:
1 + 1 = 2, 2 + 1 = 3,
which represents an arbitrary action of addition.
However, with non-reciprocal numbers defined as order in progression, 1 becomes 2 and 2 becomes 3, as the progression proceeds:
1, 2, 3, …
but what are the dimensions of these steps of progression? Ordinarily, the absence of a superscript with a number indicates that it is 1-dimensional, and we have seen that in ordinary mathematics, any number raised to the zero power is defined by the law of exponents, as the number 1, since all such numbers
n/n = n1/n1 = 11-1 = 10 = 1.
However, as we saw in the last post, this definition is problematic, theoretically, because it means that the unit cube, 13, must be defined as
n4/n1 = 14 -1 = 13 = 1
and since, in a 3D system, we can’t define the four-dimensional unit required to do this, confusion results. Fortunately, we avoid this problem in the mathematics of reciprocal numbers, because the dimensions of the numbers express their inherent dual “directions” (positive and negative), which gives meaning to 10, as a number with no degree of freedom. So, we simply start with dimension 0, at the top of the tetraktys, meaning there is no, dual, degree of freedom in the initial number of the tetraktys. It simply corresponds to a geometric point.
Ordinarily, we would regard a progression of reciprocal numbers, with two, reciprocal, aspects, as an ordered series of 0-dimensional units, or scalars, which would constitute a series of points, not 1D lines. Yet, an unexpressed exponent is assumed to equal 1. So, writing the series,
1|1, 2|2, 3|3, …
implies an exponent of 1 in the numerator and the denominator, but in this case we can’t subtract the exponent of the denominator from the exponent of the numerator, because the pipe symbol indicates that the reciprocal operation of the reciprocal number is not multiplication (division), but addition (subtraction). Therefore, the exponents must be the same in both cases, because the subtraction operation (actually sum of opposite signs) wouldn’t be valid otherwise, since we can’t subtract (add) two numbers with different exponents, or dimensions.
Yet, from our knowledge of the tetraktys, we know that the reciprocal of the scalar (dimension 0) is the pseudoscalar (dimension 3, at the 3D level, or bottom of the tetraktys). So, if one of the terms in a reciprocal number is a 0D scalar, the meaning of the pipe symbol, “|”, requires the other term to be the reciprocal of the scalar, the pseudoscalar!
We can see that this makes sense, because the series of reciprocal numbers
10|10, 20|20, 30|30, … = 00, 00, 00, …
is meaningless. A point is only its own reciprocal, when no degree of freedom is present (the n0:n0 numbers at the top of the tetraktys). Its reciprocal, with any non-zero degree of freedom, is always the pseudoscalar. Hence, the 3D pseudoscalar is the appropriate reciprocal of the 0D scalar in the Euclidean space (i.e. the 23 numbers at the bottom of the tetraktys).
Consequently, in the three-dimensional system of numbers (the Grassmann algebra), the progression of reciprocal numbers must take the form
13|10, 23|20, 33|30, …
which is a series of reciprocal numbers expressing a numerical progression of cubes, combined with reciprocally related points, corresponding to the geometric structure of Larson’s cube, with the 0D scalar at the intersection of the stack of 2x2x2 cubes.
However, because the difference between the numerator and the denominator is the difference between reciprocal quantities of different dimensions, we can express its value, as some mathematically meaningful result, only if the denominator is always the 0D scalar, while the numerator is the, reciprocal, pseudoscalar, since subtracting 0 from anything is essentially meaningless, and the breaking of the rule of exponents has no consequences in this case. As they say in the gym, no harm, no foul.
However, if we change from the pipe operation to the slash operation, then, according to the same mathematical rules, it’s possible to express the operational result as a meaningful quantity. That is to say,
13/10, 23/20, 33/30, … = 13-0, 13-0, 13-0, … = 13, 13, 13, …
Why is this? I submit that it’s because, in the slash operation, the ratio of reciprocals, as a quotient, defines the unit of a function. So, 13 is a cubic unit of the function, which equates to a cubic pseudoscalar unit per scalar unit. On the other hand, in the pipe operation, 13|10, the ratio of reciprocals defines the unit of volume, as a 3D interval, with eight directions, between the 0D point and the 3D cube.
This difference between the two operations enables us to distinguish, in an important manner, the difference between scalar magnitudes of motion, with two “directions,” and vector magnitudes of motion, in two directions. The difference in the magnitudes is the difference in the point of reference. We represent the opposite direction of a vector, by placing the arrow head at the opposite end of the line:
—————————> or <——————————
However, we represent the opposite “directions” of scalars, by placing the arrow head at both ends of a line, pointing in opposite “directions,” like this:
<————————>
This is because motion, as a 1D scalar magnitude, is an expansion from the center outward, in opposite directions, while motion, as a 1D vector magnitude, is a transference from one end of a line to the other. Thus, a scalar line always has a middle point associated with it, which is not part of a vector line. Therefore, the reciprocal number,
11|10 = 1
is a numerical expression of the double headed arrow
<————-0————->
or the result, or interval, we might say, of a 1D scalar expansion outward from a point.
By the same token, the reciprocal number,
12|10 = 12
is a numerical expression of the four headed arrow
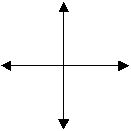
or the result of a 2D expansion from a point.
Finally, the reciprocal number
13|10 = 13
is a numerical expression of the six headed arrow
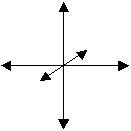
or the result of a 3D expansion from a point.
The important difference in scalar motion versus vector motion is that the two “directions” in one dimension of scalar motion produce two 1D scalar magnitudes (one in each “direction”), in one unit of time, the four “directions” in two dimensions of scalar motion produce four 2D scalar magnitudes, in one unit of time, while the six “directions” in three dimensions of scalar motion produce eight 3D scalar magnitudes, in one unit of time.
This means that to represent the unit progression of the RST, with reciprocal numbers, we write the series
13:10, 23:20, 33:30, …
where the colon symbol for ratio is used as a general symbol for reciprocity, which can be interpreted as either of the two operations we have defined. Consequently, this gives us two representations of the reciprocal operation: One is a geometric interval, and the other is a function, which produces that interval; that is, one is a representation of a scalar “distance” with two fixed, reciprocal, aspects, the scalar and pseudoscalar, while the other is a representation of a function, with two changing, reciprocal, aspects, the scalar and pseudoscalar.
On this basis, the 0D scalar progression, or scalar expansion of a point, is
10:10, 20:20, 30:30, … = 10, 20, 30, …
where the expanded scalar intervals, in, are
in = 10|10, 20|20, 30|30, … = 10, 20, 30… (0, 0, 0,…)
And the function of the scalar progression, f(p0), which produces them, is
f(p0) = Δ10/Δ10.
The 1D scalar progession, or scalar expansion, of a line, is
11:10, 21:20, 31:30, … = 11, 21, 31, …
where the expanded scalar intervals are
in = 11|10, 21|20, 31|30, … = 11, 21, 31 (<-0->, <—0—>, <—-0—->, …)
And the scalar function, which produces them, is
f(p1) = Δ11/Δ10
However, notice that this time, due to the fact that there are TWO directions in the ONE dimension, the progression of the 1D units, as opposed to the progression of the 0D units, is an increase in multiples of two 1D units, one “positive” unit, relative to zero, and one negative unit, relative to zero: 2, 4, 6, …, or the 1D progression, P1, is P1 = (2*11), (2*21), (2*31), …
Now, the 2D scalar progession, or scalar expansion, of an area, is
12:10, 22:20, 32:30, … = 12, 22, 32, …
where the expanded scalar intervals are
in = 12|10, 22|20, 32|30, … = 12, 22, 32, …
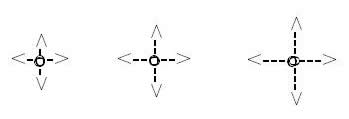
And the scalar function, which produces them, is
f(p2) = Δ12/Δ10
Again, however, due to the fact that there are TWO directions in each of the TWO dimensions, the progression of the 2D units, as opposed to the progression of the 1D units, is an increase in multiples of four 2D units, two polarized units in two independent directions, relative to zero, and two oppositely polarized units in two opposite independent directions, relative to zero: 4, 16, 36, …, or the 2D progression, P2, is P2 = (4*12), (4*22), (4*32), …
Finally, the 3D scalar progession, or scalar expansion, of a volume, is
13:10, 23:20, 33:30, … = 13, 23, 33, …
where the expanded scalar intervals are
in = 13|10, 23|20, 33|30, … = 13, 23, 33, …
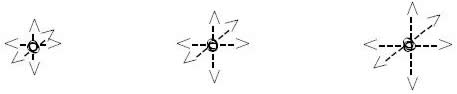
And the scalar function, which produces them, is
f(p3) = Δ13/Δ10
Now, due to the fact that there are TWO directions in each of the THREE dimensions, the progression of the 3D units, as opposed to the progression of the 2D units, is an increase in multiples of eight 3D units, four polarized units in three independent “positive” directions, relative to zero, and four polarized units in three independent “negative” directions, relative to zero: 8, 64, 216, …, or the 3D progression, P3, is P3 = (8*13), (8*23), (8*33), …
Of course, in the context of the RST, this immediately raises the possibility of the inverse of these intervals, and the functions, which produce them; that is, it is the progression of the temporal tetraktys, in the form of the temporal 2x2x2 stack of cubes. Would this take the form of
f(p-n) = Δ1-n/Δ10?
This is heavy stuff!
LRC Seminar - Explaining the Dimensions of Scalars
In the previous two posts, I’ve sketched how, in the upcoming seminar, I will approach explaining the three properties of scalar numbers that correspond to the three properties of physical magnitudes - quantity, “direction,” and dimension. Essentially, we’ve seen that it is order in reciprocal progressions that defines numerical quantity with the dual “directions” observed in nature, and that these reciprocal quantities can be arithmetically, or algebraically, combined, by resorting to two, operational, interpretations of number, symbolized by a slash and a pipe symbol, and restricting the operations of multiplication (division) and addition (subtraction) to these interpretations, respectively.
Now we come to the question of dimension, the third property of physical magnitudes that we want to define as a corresponding property of numbers. At first this might seem impossible, because scalar quantities, even those with dual “directions,” can’t be rotated as physical quantities can. Yet, while this is certainly true, we need to remember that dimensions of physical magnitudes, i.e. length, width, and depth, are simply independent variables, and that it is through the operation of rotation that the independence of these fundamental physical dimensions is established. However, nothing precludes us from establishing independence of variable quantities through some means other than rotation.
For example, three points, separated in space, are independent points, in terms of their different locations, whether those locations are confined to a one-dimensional line, a two-dimensional plane, or a three-dimensional volume. As explained in the previous posts below, combining a positive and negative quantity, in the form of two reciprocal numbers, defines a “distance,” or an interval, between them; that is,
1|2 + 2|1 = 3|3 = 0, so it follows algebraically that
1|2 = -(2|1), and
2|1 = -(1|2).
Plotting these two quantities on a number line, we get
1|2———-0———-2|1 or -1———-0———-1
So, the difference, or interval, between them is two units
(1|2) - (2|1) = -1 - (1) = -2, or
(2|1) - (1|2) = 1 - (-1) = 2.
Hence, the algebra is non-commutative, because ordinary arithmetic is non-commutative (i.e. the order of operations matters in subtraction) . But the non-commutativity of the subtraction operation is tantamount to a conservation of the “direction” property of the reciprocal number, which we have defined without recourse to an imaginary number, in the form of the square root of -1.
However, the question then arises, what is the square root of the negative quantity, 1|2? Is there a reciprocal number that when raised to the power of 2 equals 1|2? The answer is yes, there is, but to understand it requires us to delve into the meaning of raising numbers to powers and then extracting roots from them. What does it mean to raise the number 1 to the power of 2, and then extracting that power from it, as its root? We are taught in middle school that
10 = 1
11 = 1
12 = 1x1 = 1
13 = 1x1x1 = 1,
and we learn to think of the base number as a factor and the exponent as the number of factors in the product equal to the exponentiation. However, we are also taught to relate these numbers to the dimensions of a coordinate system (which Hestenes likens to catching a debilitating virus). This may be a little confusing to adults (children seldom question it), because, while 11 can readily be understood as a linear unit, 12 as an area unit, and 13 as a cubic unit, in a 3D coordinate system, how is it that 10 = 1? Logically it would follow that it should be analogous to a point at the origin of the coordinate system, but the origin has to be zero, not 1.
The way this is normally explained in terms of a binary operation is that, by a law of exponents, we understand that 11/11 = 11-1 = 10 = 1, where 1 must be understood as a dimensionless number, a unit with no dimensions (so I guess zero is defined as 01/01?!!). Yet, to a jaded adult that seems a little suspect, because 0 and 1 are quite different. Besides, if we go that route, it means that 11 = 12/11, 12 = 13/11, and 13 = 14/11, which also means that 11 * 10 = 11, or a unit line times a unit point is a unit line, and 11 * 11 = 12, or a unit line times a unit line is a unit area, and 12 * 11 = 13, or a unit area times a unit line is a unit volume, and 13 * 11 = 14, or a unit volume times a unit line is a what? A hypervolume? What’s that?
The only thing that we have accomplished, with this law of exponents, is a trade-off. We had no explanation, at one end of the tetraktys, and we traded it for no explanation at the other end of it! Besides that, in what sense is a point times a line equal to a line? Nevertheless we learn to glibly state that any number raised to the zero power is equal to one, without noting that this also requires us to believe that, in order to raise any number to the third power, we must define something as a unit that is clearly indefinable as a unit (i.e 14). Of course, we do it anyway, because, for most uses, it doesn’t affect us, and a point magnitude, somehow becoming a scalar multiplier of a line magnitude, makes sense in practice, if not in theory.
Fortunately, however, we don’t encounter the same theoretical problem with the dimensions of reciprocal numbers, because we can define dimensions, or powers of a number, as sets of dual “directions” inherent in the numbers. On this basis, we can describe four units using four numbers with increasing sets of “directions”:
10:10 = units with no dual “directions” (corresponding to geometric points)
11:11 = units with one set of dual “directions” (corresponding to geometric lines)
12:12 = units with two sets of dual “directions” (corresponding to geometric areas)
13:13 = units with three sets of dual “directions” (corresponding to geometric volumes)
where the colon is used as a generic symbol of operation, representing either the slash, or the pipe, symbol of our two operational interpretations of number.
This clarification of the definition of numerical dimensions, as simply the difference in the number of sets of dual “directions,” in a given number, makes it possible to identify a numerical, or scalar, “geometry” with the customary vector geometry of Euclidean three space, when these scalar dimensions are independent variables, which is tantamount to the definition of orthogonality in spatial dimensions.
As Larson first pointed out, with what is now called Larson’s cube, there are a total of eight “directions” possible in a 3D magnitude. These “directions” are analogous to the eight vector directions in the cube, delineated by connecting the eight corners of the cube with four diagonal lines, intersecting at the origin of the cube, when it is formed from a stack of 2x2x2 cubes, as shown in figure 1 below:
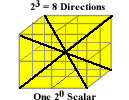
Figure 1. The Eight Directions of Larson’s Cube
In the next post, we will analyze the cube in terms of eight scalar “directions,” which, as we will see, are eight 3D scalar magnitudes, or, what is tantamount to the same thing, eight 3D numbers, completing the generalization of number as magnitude.