The New Mathematics
Towards the Unification of Algebra and Geometry
Exploring the scalar properties of the tetraktys, we are exploring fundamental concepts of magnitude, dimension and “direction.” In the last post, we saw that the numerical expansion of what we call Larson’s cube (LC), which is the geometric equivalent of the tetraktys, can be expressed as:
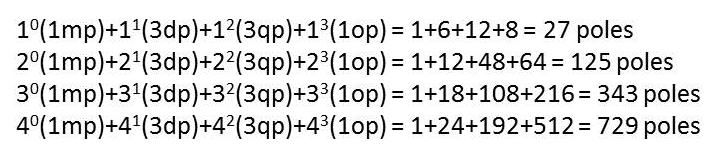
where poles are the constituent components of monopoles (mp=1), dipoles (dp=2), quadrupoles (qp=4) and octopoles (op=8). This gives us a means to express the sum of the unlike dimensions of unit numbers: In other words, we can sum the unit points, the unit areas, and the unit volumes of elements of the expanded tetraktys (1331), which is the numerical equivalent of the expanded LC, in terms of these poles.
Consequently, the numerical expression of the scalar expansion of the LC is
33, 53, 73, …(2n+1)3, n = 1, 2, 3, …∞
Now, it’s important to distinguish between this 3D expansion of the tetraktys and the 0D expansion of Pascal’s triangle, or the binomial expansion, which is normally considered as the numerical expansion of geometric dimensions, without including the notion of magnitude and “direction.” The scalar expansion of the triangle is simply,
20, 21, 22, 23, …2n, n = 0, 1, 2, 3, …∞
We can interpret this expansion as the expansion of the countable number of points:
20 = 1 instance of 1 point; 21 = 2 instances of 1 point; 22 = 2 sets of 2 instances of 1 point; 23 = 2 sets of 2 sets of 2 instances of 1 point, etc.
1) 20 = (*) = 1
2) 21 = (*)+(*) = 1+1 = 2
3) 22 = [(*)+(*)]+[(*)+(*)] = 2+2 = 4
4) 23 = {[(*)+(*)]+[(*)+(*)]}+{[(*)+(*)]+[(*)+(*)]} = 4+4 = 8
Hence, unlike the numerical expansion of the tetraktys, which is equivalent to the 3D geometric expansion of the LC, the numerical pattern of the triangle is not equivalent to any geometric expansion, but it is simply a regrouping of 0D terms. Take line four for example:
4) 23 = {[(*)+(*)]+[(*)+(*)]}+{[(*)+(*)]+[(*)+(*)]} = 4+4 = (*)+(***)+(***)+(*) = 1+3+3+1 = 8
That this sum of points in line 4 of the triangle (4+4 = 8) is equal to the sum of dimensional coefficients in the tetraktys (1+3+3+1 = 8) appears to be the cause of a colossal error in the development of mathematics: The fundamental confusion resulting from an incorrect understanding of magnitude, dimension and “direction” in mathematics and geometry, is tantamount to a detour along the road to comprehending their unity.
As a result of this non-comprehension, mathematics has been developed along a non-geometric line, leading to the confusion in the theory of algebra lamented by Hamilton, wherein he observed:
…it requires no peculiar scepticism to doubt, or even to disbelieve, the doctrine of Negatives and Imaginaries, when set forth (as it has commonly been) with principles like these: that a greater magnitude may be subtracted from a less, and that the remainder is less than nothing; that two negative numbers, or numbers denoting magnitudes each less than nothing, may be multiplied the one by the other, and that the product will be a positive number, or a number denoting a magnitude greater than nothing; and that although the square of a number, or the product obtained by multiplying that number by itself, is therefore always positive, whether the number be positive or negative, yet that numbers, called imaginary, can be found or conceived or determined, and operated on by all the rules of positive and negative numbers, as if they were subject to those rules, although they have negative squares, and must therefore be supposed to be themselves neither positive nor negative, nor yet null numbers, so that the magnitudes which they are supposed to denote can neither be greater than nothing, nor less than nothing, nor even equal to nothing. It must be hard to found a Science on such grounds as these, though the forms of logic may build up from them a symmetrical system of expressions, and a practical art may be learned of rightly applying useful rules which seem to depend upon them.
The effect of this detour probably only appears to the non-genuises (Hamilton was truly a genuis) among us, when we seek to understand the properties of scalar motion. After all, who needs to understand n-dimensional scalars in the practical world of vector motion?
In the theoretical world of nothing but motion, we have to combine n-dimensional entities of motion and determine how these combos relate to one another. We can’t do it without first clearing up the confusion in our understanding of these fundamentals.
Hopefully, it’s getting to the point that we can begin to formulate the n-dimensional, scalar algebra we need to move forward, though the very idea must appear preposterous and nonsensical to the uninitiated.
Contemplating the Mystery of Unit Expansion
Unit progression, or expansion, is the central, core consequence of the RST. It is the starting point of the universe of motion, in every sense of the word. Larson developed the idea logically, and he maintained that his development was mathematically consistent, and he insisted that a new mathematical formulation was unnecessary.
In a letter to Frank Meyer, two years before he passed away. Larson wrote:
As I have tried to emphasize throughout my writings, the conceptual aspects of physical theory, our understanding of what the mathematics of physical events mean, is independent of the mathematical relations. There are usually many possible interpretations of the same mathematics. Consequently, the true meaning cannot be derived from the mathematics. As matters now stand, the accepted physical meaning of each mathematical relation is based on assumptions applicable to that particular case. Conventional physical theory has a general mathematical structure into which each individual conclusion is required to fit, but it has no similar conceptual structure, and it therefore has no way of verifying the conceptual interpretations of the mathematical relations. Our contribution is to provide the conceptual structure that is needed. Since the previous interpretations were based on unconnected assumptions, it was inevitable that some of them would turn out to be wrong, but this does not necessarily mean that the mathematical expressions are incorrect. And where we do find that some modification of the mathematical relations is necessary, we do not need any new kind of mathematics.
However, it is evident that “a new kind of mathematics” is necessary, since the legacy mathematics has taken a development route that follows vector motion, rather than scalar motion. In vector mathematics, as in vector motion, the point’s position, relative to another, is paramount, while in scalar mathematics, as in scalar motion, the magnitude’s value, relative to another, is paramount.
However, because a vector also has magnitude, confusion in terms of the mathematical meaning of scalar, since it has been understood mostly in the context of vector mathematics, results when we speak of scalar dimensions.
This confusion is cleared up when we cast scalar dimensions in the light of the first four levels of the binomial expansion, which yields the tetraktys (2^0 = 1, 2^1 = 2, 2^2 = 4, 2^3 = 8), since we can understand the base number 2 as two “directions” of a given dimension, which produces the doubling expansion 1, 2, 4 and 8 of poles, defining the geometry of Larson’s cube (point, line, plane and cube).
However, the fact that numbers, as factors, can be expanded without limit (n x 2; n—>∞), and the fact that mathematicians regard these factors as dimensions, has led them to regard factors of 2 greater than 3 as geometric dimensions (hyper geometric dimensions), even though a child can see that the logic is bogus.
It is a fact that nature stops at three dimensions, Raul Bott proved it, so trying to ignore that limit only leads to confusion, in the end, as we see it has in LST theory, which has been stopped dead in its tracks by it (see here.) While this was not so evident in Larson’s time, it is clear to almost everyone now: the trouble with physics is that physicists have sought solutions, by following mathematicians into the realm beyond three dimensions.
Here at the LRC, we not only assert that this is a mistake, we contend that there is no need to be tempted to do it, when one understands the science of simple mathematics in terms of the science of simple geometry.
When we expand Larson’s cube, the progression is 8, 64, 216, 512…(nx2)3, where n = 1, 2, 3, …∞. In this way, the base 2 increases not as factor of 2, but as a multiple of 2, and each dimension can be expanded in turn for each successive base:
(1x2)0 = 1; (1x2)1 = 2; (1x2)2 = 4; (1x2)3 = 8,
(2x2)0 = 1; (2x2)1 = 4; (2x2)2 = 16; (2x2)3 = 64,
(3x2)0 = 1; (3x2)1 = 6; (3x2)2 = 36; (3x2)3 = 216,
(4x2)0 = 1; (4x2)1 = 8; (4x2)2 = 64; (4x2)3 = 512.
Figure 1. Expansion of Larson’s Cube (LC).
This is scalar magnitude expansion in 0, 1, 2 and 3 dimensions. Each dimension has two “directions,” and the expansion proceeds step by step, as the natural, or counting numbers increase, according to the dimensional number of the term.
Since the expansion is eternal, picking a point in the count is tantamount to starting at the number one and increasing from there.
The unit number, 1, is the number 2 expanded from a point, 10, to a 2x2x2 = 8 stack of unit cubes, but all three dimensions, the line, the plane and the cube expand simultaneously in two “directions”, four “directions,” and eight “directions,” respectively (the point doesn’t expand, of course.) This gives rise to the numbers of the fourth line of Pascal’s triangle, 1331, which, when summed, equal 8.
This composite number, the tetraktys, or its geometric equivalent, the LC, can be understood as the 3D unit scalar and, if it is treated as such, it is clear that the subsequent lines of the expanded triangle are multiples of it, as we have already discussed in the previous post.
However, to treat the subsequent lines of the expanded triangle, line 5 and up, as 2n geometric dimensions, or as some kind of “extra” geometric dimension, is a grave error for physicists, who, we contend, must respect the limits of Euclidean geometry in their study of the structure of the physical universe, if they expect to progress.
Taking the binomial expansion of the tetraktys, the 2x2x2 = 23 = 8 unit cubes, and the corresponding 1mp+3dp+3qp+1op = 27 poles, as the fundamental scalar unit of our new system of mathematics, replacing the number 10, as the fundamental scalar unit, as understood in today’s mathematics, to which mathematicians then add “imaginary” numbers to this “real” number, in order to increase its dimensions, requires much of us to be sure, but it seems to me that it must be done, if we are to progress in our understanding of the physical universe.
All righty then.
Comparing the LC pseudoscalar expansion, 8, 64, 216, 512, …, to the triangle pseudoscalar expansion, 8, 16, 32, 64, …, it’s hard to see much of a correlation between the two. Whereas the sum of the numbers of a given line of the triangle is always equal to the pseudoscalar of that line, which is always a power of 2, and the sum of the number of poles of a given line is always equal to a power of 3, the sum of the number of poles of each successive LC expansion doesn’t follow this pattern, rather it follows a (2n+1)3 sequence: 33, 53, 73, etc.
So, while it’s easy to see that the tetraktys (1331) is a unit of the triangle and can be used to calculate its expansion, either the expansion of its numbers, or the expansion of their associated dimensions, when these are understood in the 3D terms of the tetraktys, the question now is, “Can we relate the tetraktys to the expansion of the LC, which has a different pseudoscalar than that of the triangle?”
Happily, the answer is yes. In fact, it is simple: We just need to join the tetraktys numbers with the dimensions of the LC expansion, as shown in figure 1 above, and voila, it appears:
Figure 2. The Expansion of the Tetraktys and Larson’s Cube
There is much more work to do, but understanding how the dimensions of the tetraktys relate to the expansion of Pascal’s triangle AND the expansion of the LC and the implications of this for today’s mathematics and physics is a necessary step toward the development of a “new kind of mathematics.”
I think Larson would be happy, cautiously happy, but happy nonetheless.
They Say Beauty is in the "i" of the Beholder
(-) (+)
2^0 = 1 is the magnitude of the point in the middle, 1/1, and 2^1 = 2 is the one dimensional magnitude, with two opposite polarities, or a dipole, stretching out on either side of the point. In other words, it is the numerical equivalent of a geometric line in one dimension.
Hamilton finally realized that he needed four terms to construct what he thought of as a 3D algebra, moving one dimension up from what he thought of as a 2D algebra. He suddenly realized one day that he could accomplish his objective with one real number and three imaginary numbers, or what mathematicians would call a 4D number a+ib+jc+kd.
Today, these numbers are called quaternions (ℍ), and Baez refers briefly to the battle that ensued as to whether these allegedly “4D” quaternion numbers, or the allegedly “2D” complex numbers were the numbers of choice to use in science and engineering.
The champions of (ℍ) lost, and (ℍ) descended into the dusty bin of academics for a long time, but the important thing to understand is that they are actually 2D numbers, not 4D numbers! Think of them as a scalar, s, and a 3D vector, v (or s,v).
They correspond to the third line of the tetraktys (121), which, in binomial expansion form, is the numerical equivalent of a geometric 2D area: 1(2^0), 2(2^1), 1(2^2), because it consists of one center point, and two, orthogonal, dipoles, extending out from it, forming one quadrupole.
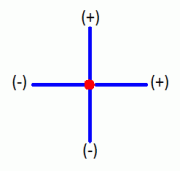
Increasing line 3 of the tetraktys to line four (1331) gives us a true 3D numerical equivalent of a geometric volume, which, as Hamilton’s friend Graves pointed out to him, could be formulated with seven imaginary numbers, but neither Hamilton nor Graves realized that these constructions, now called octonions, O, were in the true 3D level of the tetraktys, which we at the LRC now know is the numeric equivalent of the 2x2x2 stack of unit cubes, which we call Larson’s cube, containing one 2^0 point in the middle, three orthogonal dipoles, three orthogonal quadrupoles and one octopole, or 1(2^0), 3(2^1), 3(2^2), 1(2^3), in terms of the binomial expansion.
This is where the professor stomps his foot, because Baez and company apparently don’t recognize this. Instead they take the 8 corners of a 1x1x1 = 1 unit cube, not a 2x2x2 = 8 stack of 1-unit cubes, and they assign 7 of the 8 corners of the cube (poles) to the 7 imaginary numbers of Graves 9 (omitting the scalar a=1), and from this they devise a way to concoct the last remaining normed division algebra that can be constructed.

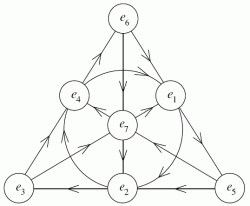
It’s complicated and a total distortion of the true nature of the tetraktys (they collapse their cube into a Fano plane.) This is not how we understand the tetraktys in terms of the binary expansion and its numerical equivalents of the geometric point, line, area and volume, forming Larson’s cube.
But what is very useful is the recognition that the four sums of the numbers of each the of the tetraktys, define the first four lines of Pascal’s triangle,
1 = 1
1+1 = 2
1+2+1 = 4
1+3+3+1 = 8
and which they call “dimensions,” limits the number of normed division algebras to these four geometric real dimensions, 0,1,2 and 3. This is the tetraktys and it contains all the geometric entities of our 3D universe, corresponding to the point, the line, the area and the volume. It’s a case of numbers confirming the first postulate of the RST, which states that everything consists of one component, existing in three dimensions (“Hear oh Israel, the Lord our God, the Lord is One.”)
Moreover, because of their mathematical concept of the single unit cube, with its 8 corners, defining the algebra of octonions, they assume that the next line of Pascal’s triangle (14641), leads to a fourth geometric dimension (24) in the form of the first hypercube, and they don’t stop there, but continue to higher dimensional hypercubes, collapsing them into a plane and studying their properties with group theory and Lie algebras.
To us, this is a grievous mistake, or at least unnecessary, not only because it misses the point of the identification of the binomial expansion with the magnitudes, dimensions and polarities of the tetraktys, geometrically expressed in the form of Larson’s cube, but also because it hides the real implications of Bott periodicity.
Baez explains Bott periodicity as the reason the number 8 is one of his three favorite numbers, but he can’t explain why this number is so significant, no one can, unless they admit that it reflects the fact that the physical universe is limited to three dimensions, geometrically speaking, as stated in the RST fundamental postulates.
If they would only admit this limitation, they would understand that lines 5 and up of Pascal’s triangle should be interpreted as compounds of line 4 of the triangle. In other words, lines 5 and up are multiples of the 3D line 4.
1) 1 = 1
2) 1+1 = 2
3) 1+2+1 = 4
4) 1+3+3+1 = (6+2) = 8
5) 2(1+3+3+1) = (12+4) = (1+4+6+4+1) = 16
6) 4(1+3+3+1) = (24+8) = (1+5+10+10+5+1) = 32
.
.
.
Thus, the true nature of Bott periodicity is seen in the scalar expansion of three dimensions in the form of Larson’s cube, which can best be understood as the linear expansion of a 1-unit dipole as the independent variable, with the 4 quadrupoles and 8 octopoles, as dependent variables.
Also, since two of the three dipoles and quadrupoles are degenerate in the nxnxn stack, we only need scale 1 each of them, as we go up each step of the triangle. Hence, starting with line 4 and renumbering, the Larson cube expands as:
1) 1^1(2^1) 1^2(2^2) 1^3(2^3) ~ 1 2x2x2 = 1dp, 1qp, 1op
2) 2^1(2^1) 2^2(2^2) 2^3(2^3) ~ 1 4x4x4 = 2dp, 4qp, 8op
3) 3^1(2^1) 3^2(2^2) 3^3(2^3) ~ 1 6x6x6 = 3dp, 9qp, 27op
4) 4^1(2^1) 4^2(2^2) 4^3(2^3) ~ 1 8x8x8 = 4dp, 16qp, 64op
.
.
.
We can see from this that the doubling of the sums of the steps in Pascal’s triangle, is due to the counting of the redundancy in the expansion of the 2x2x2 stack: there are ALWAYS 3 dipoles and 3 quadrupoles in the expanded stacks, so if we count all these entities, we get (counting just the number of entities, the bolded coefficients):
1) 1(2*0) + 3(2^1) + 3(2^2) + 1(2^3) = 8
2) 2(2*0) + 6(2^1) + 6(2^2) + 2(2^3) = 16
3) 4(2*0) + 12(2^1) + 12(2^2) + 4(2^3) = 32
.
.
.
Hence, we see clearly what has happened. The numbers in the expansion of Pascal’s triangle seem to be a reflection of the 3D expansion of Larson’s cube, not an n-dimensional expansion of a hypercube, as Baez and company see it.
Nevertheless, while the sums of the four 3D coefficients in the expansion of the initial LC (1331) match the sums of the successive lines in Pascal’s triangle, when they are doubled, the sums of the products of the coefficients with the respective n-dimensional entities do not match, except in line 4 (our line 1.)
1) 1(2^0) + 3(2^1) + 3(2^2) + 1(2^3) = 8 (27=27)
2) 2(2^0) + 6(2^1) + 6(2^2) + 2(2^3) = 16 (54 vs 81)
3) 4(2^0) + 12(2^1) + 12(2^2) + 4(2^3) = 32 (108 vs 243)
.
.
.
As explained in the previous post, to match the sums of the products, the coefficients of line 4 must be tripled in order to match the triangle, not doubled. So, to match the sum of the triangle’s coefficients (2n), we double the 3D coefficients, at each line (a power of 2), but to obtain the sum of the products of the coefficients and the n-dimensional entities, we have to triple the coefficients (a power of 3).
It’s weird, but it’s probably due to the fact that the coefficients contain the degeneracies of the dipoles (3) and quadrupoles (3) within the LC. To reconcile this conflict, we can use the triangle’s coefficients and the LC’s n-dimensional entities, even though we can’t identify them explicitly in a geometric figure, yet.
1x20, 3x21, 3x22, 1x23 = 1 + 6 + 12 + 8 = 27
1x20, 4x21, 6x22, 4x23, 1x(21x23) = 1 + 8 + 24 + 32 + 16 = 81
1x20, 5x21, 10x22, 10x23, 5x(21x23), 1x(22x23) = 1 + 10 + 40 + 80 + 80 + 32 = 243
1x20, 6x21, 15x22, 20x23, 15x(21x23), 6x(22x23), 1x(23x23) = 1+12+60+160+240+192+64 = 729
1x20, 7x21, 21x22, 35x23, 35x(21x23), 21x(22x23), 7x(23x23), 1x(21x23x23) = 1+14+84+280+560+672+448+128 = 2187
Notice, that we have broken down the terms with dimensions greater than three into subterms of dimension three or less, to respect the limits of Bott periodicity and the RST.
Even though it’s difficult to see how all these n-dimensional entities could possibly be assembled into one compound geometric figure, one thing is clear: The sum of the products of the triangle’s coefficients and the n-dimensionals of the cube are powers of 3, starting with the initial LC, 1331.*
Since we can now obtain the same result with the LC, we can re-write the expansion as:
LC0 = 33
LC1 = 3(LC0) = 34
LC2 = 3(LC1) = 35
LC3 = 3(LC2) = 36
LC4 = 3(LC3) = 37
which is a lot better than writing:
1x20, 3x21, 3x22, 1x23 = 1 + 6 + 12 + 8 = 27
3x20, 9x21, 9x22, 3x23 = 3 + 18 + 36 + 24 = 81
9x20, 27x21, 27x22, 9x23 = 9 + 54 + 108 + 72 = 243
27x20, 81x21, 81x22, 27x23 = 27 + 162 + 324 + 216 = 729
81x20, 243x21, 243x22, 81x23 = 81 + 486 + 972 + 648 = 2187
What the implications are of this clarification of scalar magnitudes, directions, and dimensions is hard to tell at this point, but my guess is that they are significant.
* Update: Turns out that this is not correct. I should have checked it. Please see my reply to Horace in the comments below.
The Trinity - A Christmas Gift
In the New Physics blog, we announced the exciting development (or latent discovery) that the ratio of the continuous magnitudes of Larson’s Cube (LC), which contains the unit ball of the SUDR (r = 1/31/3) and is contained by the unit ball of the TUDR (r= 31/3), is equal to the total number of poles in the 3D tetraktys:
Equation 1: (2^0 + 2^1 + 2^2 + 2^3) = 27
This is exciting because it relates the discrete numbers of the tetraktys to the continuous magnitudes of LC. But to understand it, one has to understand the equation above. It is an equation of what we call the Reciprocal System of Mathematics (RSM).
In the legacy system of mathematics, the sum of the numbers in equation 1 above is 15, not 27. In the RSM, the base number 2 in the binomial expansion is the magnitude’s number of “directions” (think polarities) and its exponent is the number of its dimensions.
This relates to Pascal’s triangle and Clifford algebras, but also to Raul Bott’s periodicity theorem, which limits the number of geometric dimensions to no more than three. The key is to understand that each number represents the number of geometric entities of 2n (n = 0-3), contained in a given dimension, where the dimension is the number of terms in the equation, less 1.
Thus, in equation 1 above, the total number of terms is 4, so the dimension is 3 and there is one 20 term contained in that dimension, three 21 terms, three 22 terms, and one 23 term. These happen to be the four coefficients of the fourth line of Pascal’s triangle, the sum of which is the mysterious number 8 of Bott periodicity:
Line 1) = 1 = 1
Line 2) = 11 = 2
Line 3) = 121 = 4
Line 4) = 1331 = 8
Since these numbers correspond to the first four dimensions of the binomial expansion and Clifford algebras, and they correspond to the geometry of Larson’s 2x2x2 stack of unit cubes, the philosophy of the ancient Greek tetraktys, and the dimensions of the only known normed division algebras, not to mention the blades of Hestenes’ Geometric Algebra, and the domain of string theory, our interpretation of them as the “directions” in the geometric dimensions of numeric magnitudes is in good company.
Hence, we can rewrite equation 1 above to reconcile the RSM and legacy math difference, by combining the coefficients of Pascal’s triangle with the terms of the binomial expansion:
Equation 2: 1(2^0) + 3(2^1) + 3(2^2) + 1(2^3) = 27
However, the coefficients of the fifth line of Pascal’s triangle, corresponding to the fourth dimension (5 terms less 1), are
Line 5) 14641 = 16
Obviously, the coefficients of each line of the triangle sum to powers of 2, while the sum of the products of the coefficients and the n dimensional geometric entities are powers of 3. For example , the sum of the products of the fourth dimension is:
Line 5) 1(2^0) + 4(2^1) + 6(2^2) + 4(2^3) + 1(2^4) = 3^4 = 81.
The coefficients of the triangle’s fifth dimension are
Line 6) 1 5 10 10 5 1 = 2^5 = 32
and the sum of the products of the coefficients and the n dimensional entities is
Line 6) 1(2^0) + 5(2^1) + 10(2^2) + 10(2^3) + 5(2^4) + 1(2^5)= 3^5 = 243.
But since our RSM interpretation counts the number of n-dimensional entities contained in each dimension, and those dimensions cannot exceed 3, what meaning can the triangle’s lines 5 and up have for the RSM?
Well it turns out to be the key to the RSM actually. Because the sum of the products of the triangle’s coefficients and the n-dimensional geometric entities is always a power of 3, we can simply multiply each coefficient of line four (the 3rd dimension) of the tetraktys by 3 to obtain the next higher set of coefficients, thus preserving the four terms of the three-dimensional form:
Line 5) 1331 x 3 = 3+9+9+3 = (8 x 3) = 24
Line 6) 3993 x 3 = 9+27+27+9 = (24 x 3) = 72
Line 7) 9 27 27 9 x 3 = 27+81+81+27 = (72 x 3) = 216
Notice that this is tantamount to multiplying the number of geometric entities of the LC by the number 3.
So much for obtaining the coefficients. Now, what about the sum of their products with the n-dimensional geometric entities?
Well, as we have already seen, these are just powers of 3:
Line 4) 3^3 = 27
Line 5) 3^4 = 81
Line 6) 3^5 = 243
Line 7) 3^6 = 729
So, we have another periodicity. This time it is a period of 27. We will call it the tetraktys periodicity. Therefore, in the RSM, the number 8 of Bott periodicity, which is really the sum of the four coefficients of the triangle’s fourth line, is related to the number 27 of the tetraktys periodicity, which is really the sum of the four coefficients’ products with the corresponding four n-dimensional entities of the tetraktys (LC,) by the number 3, which is the key factor of both periodicities, uniting the discrete periodicity with the continuous periodicity.
This is a wonderful gift, a gift of 3, the trinity we might say, one which we neither understand nor deserve, but which we celebrate this time of year.
The Algebra of Scalar Motion
Assuming a 3D oscillation of space and an inverse 3D oscillation of time, called space unit displacement ratio (SUDR) and time unit displacement ratio (TUDR), respectively, we have combined them into SUDR|TUDR (S|T) units, which we then use as preons to construct a model of particles corresponding to the particles of the LST community’s standard model of particle physics.
Of course, the standard model is based on the Newtonian system of theory, which, based on vector motion, constitutes his program of research to find the fewest number of particle interactions among the fewest number of particles, in the structure of the physical universe.
Though the LST community has successfully modified the concept of vector motion considerably, substituting the description of a particle’s state, by means of its “probability amplitude,” in space and time, for the description of a particle’s state, by means of its change in position, in space and time, they have done so with an algebra Sir William Rowan Hamilton regarded as non-intuitive, unscientific and even self-contradictory, in contrast to Euclidean geometry (see here.)
Larson excluded the RST community from using this defective algebra, when he formulated the second fundamental postulate and included in it the assumptions of Euclidean geomety and the “relations of ordinary commutative mathematics.”
Some have argued that the word “ordinary” is too vague a term, that he should have been more explicit, but it’s clear that he was referring to the unfamiliar rule for multiplication that had emerged in connection with quantum physics, during his formative years. It was this rule, the rule of non-commutative multiplication, where p times q is not equal to q times p, which was known to mathematicians familiar with matrix multiplication, but not to most physicists, which enabled the science of quantum mechanics from that point on.
It was based on multiplying the amplitudes of two oscillations in order to calculate the energy involved. If the rule of ordinary commutative mathematics were used in these calculations, the result was an infinite sum in a Fourier series. The solution was to use non-commutative multiplication, something that disconcerted physicists, but not mathematicians.
Larson was good at mathematics, but he was not interested in the philosophy of the subject. He was interested in getting away from the necessity of using partial differential equations (PDEs), and the attendant “playing with variables” to find solutions to physical questions. He sincerely believed that there had to be a better way and he sought to find it in the observable world of Euclidean geometry, absolute magnitudes and ordinary commutative mathematics.
However, as we have studied the consequences of the RST postulates at the LRC, and in working to develop a new theory based on them, we have discovered the work of Hamilton in mathematics, the very man who coined the terms “vector” and “quaternion.” In the process, we discovered the work of Hestenes, who laid out the development of algebra, from the days of Hamilton, in terms of key concepts of Grassmann and Clifford, which has led to our ideas of unit time and space displacements, which have two interpretations, the quantitative (-1, 0, +1), and operational (1/2, 1/1, 2/1) interpretations.
All of this was studied in terms of the tetraktys, which ended up allowing us to unify the mathematical concepts of magnitude, dimension and “direction,” with the corresponding geometrical concepts of point, line, area and volume. The effort ever since then has been to understand our RST-based physical theory in terms of this unified view of mathematics and geometry.
The result has been gratifying to say the least. We have even received a couple of substantial private awards, from those who have followed our efforts and wanted to encourage the work, but, now, we are at the point of having to understand how to add, subtract, multiply and divide with the numbers of the tetraktys that we have developed. We need an “ordinary commutative mathematics,” a multi-dimensional, scalar, algebra, if you will, to enable us to combine units of scalar motion and calculate the relations between them. In short, we need an algebra of multi-dimensional scalar motion.
With an algebra of multi-dimensional scalar motion, we can combine our preons into the bosons of photons, and then combine these into fermions of quarks and leptons, and then combine these into the elements of matter and anti-matter. Such an algebra will enable us to calculate the properties of each of these entities with a precision equal to, if not greater than, the precision obtained in quantum mechanics, but with unprecedented conceptual clarity.
We have made a lot of progress in establishing the fundamentals of the scalar algebra. One important milestone is the identification of the multi-dimensional numbers of the tetraktys with the geometric structure of Larson’s Cube (LC), which has enabled us to describe the S|T units in terms of discrete and continuous magnitudes. This way, we can do calculations, using the discrete numbers of the LC’s lines, squares and cubes, and then we can transform these into the corresponding continuous numbers that we have found in the ratios of its nested radii, surfaces and volumes.
An important indication that we are not wasting our time is the recent derivation of Einstein’s famous mass —> energy equation from the fundamental components of the S|T units. This was done by simply writing the two reciprocal units of the S|T unit as follows:

Figure 1. Einstein’s Equation in Terms of the S|T Unit of Scalar Motion
Since the photon in the LRC’s theory consists of one or more of these S|T units, we now have to calculate the different frequencies possible and their associated energy and how these bosons relate to the fermions, but it’s interesting to see that the properties of the preon of the fermion, photons in our theory, conform to the fundamental energy equation of mass and energy, as shown here.
Horace pointed out that the equations in the graphic made no sense. He was right. I uploaded the wrong graphic.
The new graphic shows the crucial step I left out in the previous one. As Larson pointed out, the intrinsic scalar motion of matter is actually s/t motion, while the measurement of that motion is actually a measurement of the resistance to that motion (inertia).
Thus, in Einstein’s mass-energy equation, the dimensions of mass are used, which are actually the inverse of the dimensions of matter, and that’s why the equation works.
I posted a new excellent video in LRC Lectures Online by John Baez that explains the LST view of the mathematics that is so important to understand, as background to the development of an RST-based theory of particle physics here at the LRC.
In his video, John talks about the tetraktys, but he doesn’t call it that. He tells the math history of imaginary numbers and their use to devise higher-dimensional algebras from the reals. He explains the important concept of normed division algebras and how they only exist in certain dimensions, and how that fact kept Hamilton frustrated for a long time, as he sought to find a three-dimensional normed division algebra (although he didn’t have a label like that to express it concisely). “Normed,” in this context, means that the absolute value of the products is equal to the product of the absolute values.
The problem is, Baez and company have changed the meaning of the word dimension, without explicitly pointing it out to non-specialists. Their use of the word doesn’t necessarily refer to geometric dimensions, but, like Larson explained, the word dimension, for them, means the number of independent magnitudes in an equation.
Thus, complex numbers (ℂ) are two dimensional numbers for modern mathematicians, because they consist of a real and an imaginary part (a+ib), and they are used in calculations of 2D rotation.
However, in terms of the RSM, line 2 of the tetraktys (11), or 1(2^0), 1(2^1) in its binary expansion, defines a one-dimensional line: